1. Diagramme de Laue
Les rayons X focalisés en F sont polychromatiques. Certains traversent le cristal en O pour donner une tache centrale noire en H sur une plaque photographique.
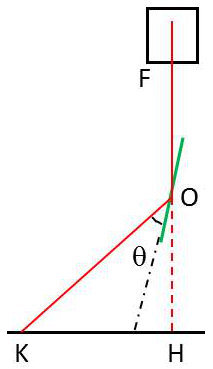Il existe une infinité de plans réticulaires faisant avec les rayons incidents des angles différents.
Il résulte que pour certains plans l’intensité du rayonnement est renforcée par interférence des rayons secondaires. Ils sont marqués sur la plaque photographique par des taches peu nettes entourant la tache centrale.
Dans le cas de la figure, on ne s’est intéressé qu’à un plan réticulaire et on voit que l’on peut écrire : \[\tan(2\theta)=\frac{HK}{HO}\]
La méthode de Laue permet donc d’étudier la symétrie du réseau cristallin et de déterminer l’orientation de plaquettes découpées dans un cristal sans égard à ses éléments de symétrie.
De Broglie a utilisé ce procédé pour comparer les diverses longueurs d’onde qui composent le faisceau de rayons X. En effet : \[\left\{ \begin{aligned} &2d\sin(\theta)=p\lambda\\ &2d\sin(\theta')=p\lambda'\\ \end{aligned} \quad\Rightarrow\quad \frac{\lambda'}{\lambda}=\frac{\sin(\theta')}{\sin(\theta)} \right.\]
2. Diagramme de Debye-Scherrer
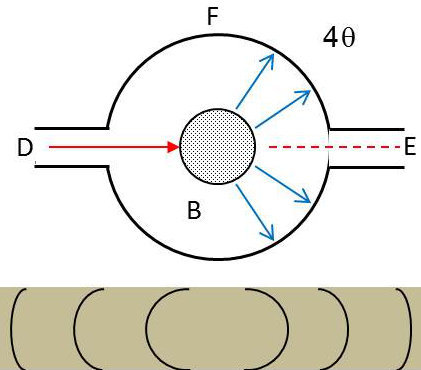On utilise un cristal broyé (poudre) attaqué par un rayonnement monochromatique. Les cristaux, comprimés en un bâtonnet B acquièrent des orientations variées, ce qui augmente les chances d’interférences qui dépendent des relations de \(\lambda,~d,~\theta\).
On obtient ainsi, non pas des taches isolées, mais des séries de taches qui, en se rejoignant, donnent des figures courbes sur le film F.
La chambre est de forme cylindrique et le film F est appliqué suivant la courbure interne de la chambre. Les rayons primaires entrent dans la chambre à travers le diaphragme D, frappent le bâtonnet B et ressortent par l’ouverture E.
Les rayons secondaires interfèrent en divergeant du bâtonnet. Les rayons, renforcés par les interférences, donnent une série de cônes et coupent le film cylindrique. On obtient ainsi des courbes intersections de ces cônes avec le cylindre.
Il est évident que les angles d’ouverture sont \(4~\theta\) si on se réfère au dispositif de Laue.
Si D est le diamètre du film, on a : \[\frac{l}{\pi~d}=\frac{4~\theta}{360}\quad\Rightarrow\quad\theta=k~l\quad\text{avec}~~k=\frac{90}{\pi~d}\]
Avantages de cette méthode
Ce système présente l’avantage d’être adapté à l’étude des sources larges, peu intenses, en employant sans aucune fente une lame cristalline de mica courbée suivant un cylindre circulaire C d’axe O.
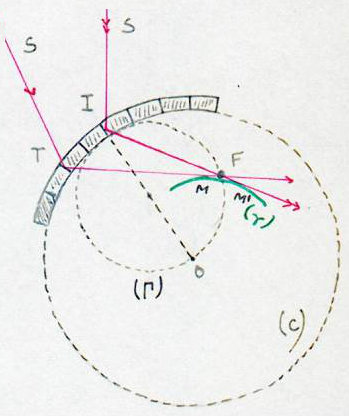Les plans réticulaires P, normaux aux faces du cristal, s’orientent alors de façon à passer tous par l’axe O du cylindre C.
Dans le plan de symétrie normal à l’axe du cylindre, il existe pour chacun d’eux un rayon SI qui donne lieu à la réflexion sélective sous l’angle \(\theta\) et tous les rayons réfléchis IR faisant le même angle \(\theta\) avec le rayon correspondant OI du cylindre enveloppant MM’.
L’arc occupé par le cristal n’étant jamais très étendu, tous ces rayons passent très près de F, sommet de MM’, F se comporte alors comme un foyer.
Pratiquement \(:\widehat{OFT}=\) 90°. Lorsque \(\lambda\) (donc \(\theta\)) varie, F décrit un cercle \((\gamma)\) de diamètre OT. C’est le cercle de focalisation sur lequel on dispose le film photographique, pour obtenir un spectre dont toutes les raies sont simultanément nettes.
3. Méthode du cristal tournant
La méthode du cristal tournant est une combinaison de la méthode de Laue et de Debye. On utilise un cristal unique et un rayonnement monochromatique. On peut photographier les raies caractéristiques du métal donc mesurer \(d\) si \(\lambda\) est connu et inversement.
Dans un même cristal, les diverses familles de plans réticulaires donneront différentes valeurs de \(d\), caractéristiques du cristal. Par exemple, pour un cube : \[\left\{~d,~\frac{d}{\sqrt{2}},~d\sqrt{3}~\right\}\]
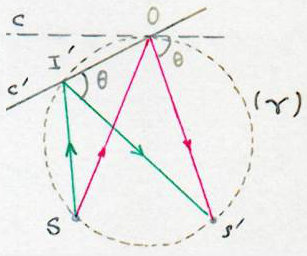
Le cristal tourne très lentement autour d’un axe O contenu dans un plan réticulaire. Pour certaines positions, la condition de Bragg est satisfaite ; lorsque \(C\rightarrow C'\), pour déterminer I’ caractéristique en incidence de Bragg, il faut que l’on ait \(\widehat{SI'S'}=\pi-2\theta\).
Le lieu de I’ sera donc un cercle passant par O, S, S’.
Tous les rayons relatifs à \(\theta\) passent donc par S’ où on obtiendra une image nette. Pour un autre \(\theta\) de Bragg, on aurait un autre S’ tel que \(OS' = OS = cte\).
La plaque photographique devra donc être un cylindre d’axe O. On obtient des surfaces coniques qui donnent sur le film cylindrique un groupe de raies horizontales.
4. Valeurs absolues des longueurs d’onde
Le calcul de \(\lambda\) suppose que d (distance inter-réticulaire) soit connue. Considérons par exemple un cristal \(Na^+Cl^-\). Pour les molécules, il y a 2N centres diffringents (\(N = 6,02~10^{1023}\)) répartis aux sommets du réseau cubique.
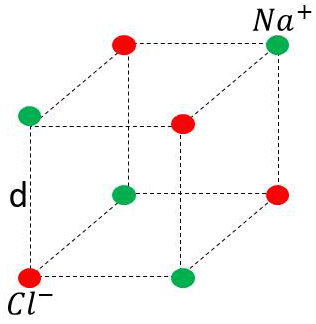Le cube élémentaire a pour volume d³, et a 8 sommets communs à 8 cubes. La valeur de la molécule gramme est donc 2N d³.
Si M est la masse molaire du sel étudié (ici 58,4) et \(\rho\) sa masse spécifique (ici 2,16 à 20°C) : \[2N~d^3=\frac{M}{\rho}\quad\Rightarrow\quad d=\sqrt[3]{\frac{1}{2N}\frac{M}{\rho}}\]
Numériquement : d = 2,8144 Å.
Il suffit d’écrire ensuite que : \[p\lambda=2d\sin(\theta_p)\qquad\theta_p~\text{mesurable}\]
