1. Introduction

Un oscillateur est un système capable de maintenir au cours du temps une loi de variation périodique pour l’un au moins des paramètres qui définissent son état. Le nombre de paramètres variables définit le nombre de degrés de liberté de l’oscillateur.

Nous aurons à considérer des oscillateurs à un degré de liberté (pendule), des oscillateurs à deux degrés de liberté ou systèmes couplés (pendules couplés par un ressort), des oscillateurs à N degrés de liberté (filtres électriques et mécaniques), enfin des oscillateurs à une infinité de degrés de liberté (cordes vibrantes).

Nous étudions dans ce chapitre les systèmes oscillants les plus simples ne comportant qu’un seul degré de liberté.

2. Oscillateur harmonique ou sinusoïdal

Un oscillateur est harmonique si sa loi de temps est : \[x(t)=a~\cos(\omega~t+\varphi)\]

La fréquence des vibrations acoustiques est comprise entre 20 et 20 000 cycles par seconde (ou Hertz), celles des ondes hertziennes (radio) entre \(10^5\) Hz et \(10^{10}\) Hz et celle du diapason qui donne le la 3 est fixée à 435 Hz.

2.1. Loi de force

Soit un point matériel \(M\), de masse \(m\), qui se déplace sur l’axe \(Ox\) suivant la loi : \[x(t)=a~\cos(\omega~t+\varphi)\]

En effectuant deux dérivations successives : \[x"+\omega^2=0\]

On peut vérifier que ce mouvement est obtenu par l’action d’une force proportionnelle à l’élongation soit \((k > 0)\) : \[F=-k~x=m~\frac{d^2x}{dt^2}\]

par application du principe fondamental de la dynamique.

On obtient effectivement : \[\frac{d^2x}{dt^2}+\frac{k}{m}~x=0=x"+\omega^2~x\]

L’intégrale générale est bien \(x=a\cos(\omega~t+\varphi)\), où \(a\) et \(f\) dépendent des conditions initiales et où \(\omega=\sqrt{k/m}\).

En résumé :

La loi de force de l’oscillateur harmonique est \(F=-kx~~;~~k>0\). Réciproquement, tout oscillateur dont la loi de force est \(F=-kx~~;~~k>0\) est harmonique.

Puisque \(k > 0\), la force est une force de rappel vers l’origine O.

2.2. Énergie de vibration

Calculons le travail élémentaire de la force \(F\) dans le déplacement \(dx\) : \[dW=F~dx=-k~x~dx=d\Big(-\frac{k~x^2}{2}\Big)\]

Posons : \[d\Big(-\frac{k~x^2}{2}\Big)=-dE_p\quad\Rightarrow\quad E_p=\frac{k~x^2}{2}+cte\]

Nous reconnaissons dans cette expression l’énergie potentielle de l’oscillateur dans le champ de forces \(F=-k~x\).

Calculons le travail élémentaire de la force \(F\) par le théorème des forces vives : \[dW=\Big(m~\frac{d^2x}{dt^2}\Big)~dx=(m~v)~dv=d\Big(m~\frac{v^2}{2}\Big)\]

Posons : \[d\Big(m\frac{v^2}{2}\Big)=dE_c\quad\Rightarrow\quad E_c=m~\Big(\frac{v^2}{2}\Big)\]

\(E_c\) est l’énergie cinétique de l’oscillateur.

La comparaison entre les deux expressions du travail élémentaire montre que : \[dE_c+dE_p=0\quad\Rightarrow\quad E_p+E_c=E=cte\]

\(E\) est l’énergie totale de l’oscillateur. Au cours du mouvement, il peut y avoir transformation de l’énergie cinétique en énergie potentielle et inversement, mais leur somme reste toujours constante et égale à l’énergie totale \(E\) de l’oscillateur.

Calculons cette énergie (constante) : \[v=0\quad\Rightarrow\quad E_c=0\quad;\quad E_p=k~\frac{a^2}{2}=m~\frac{\omega^2~a^2}{2}\]

L’énergie de vibration de l’oscillateur est donc : \[E=m~\frac{\omega^2~a^2}{2}\]

Elle est proportionnelle au carré de l’amplitude.

2.3. Généralité de l’oscillateur harmonique

Nous allons nous intéresser aux petits mouvements autour d’une position d’équilibre stable. Soit \(O\) cette position d’équilibre que nos prenons pour origine des abscisses. Puisqu’il y a équilibre, on peut écrire \(F(0)=0\).

La stabilité de l’équilibre exige d’autre part que, si on déplace le point de sa position d’équilibre, la force \(F\) tend à l’y ramener. Par suite, pour tout déplacement virtuel \(x\) de signe quelconque à partir de \(O\), le travail de la force de rappel est : \[dW<0\quad\Rightarrow\quad dE_p=-dW>0\]

L’énergie potentielle croît par conséquent lorsqu’on écarte le point \(M\) de sa position d’équilibre. Elle est donc minimum en \(O\).

Supposons continue la loi de force et développons \(E_p\) en série de Mac Laurin : \[E_p(x)=E_p(0)+\frac{x}{1!}~\Big(\frac{dE_p}{dx}\Big)_0+\frac{x^2}{2!}~\Big(\frac{d^2E_p}{dx^2}\Big)_0+\dots\]

Du fait que \(E_p\) est minimale en \(O\), on a : \[\Big(\frac{dE_p}{dx}\Big)_0=0\quad;\quad \Big(\frac{d^2E_p}{dx^2}\Big)_0>0\]

On a donc : \[E_p(x)=E_p(0)+\frac{x^2}{2!}~\Big(\frac{d^2E_p}{dx^2}\Big)_0+\dots\]

Comme : \[F(x)=-\frac{dE_p(x)}{dx}\]

alors : \[F(x)=-x~\Big(\frac{d^2E_p}{dx^2}\Big)_0+\dots\]

Posons \(K=\cfrac{d^2E_p}{dx^2}\) ; on retrouve, au second ordre près, si \(x\) est infiniment petit principal, la relation \(F(x)=-K~x\).

Par suite, à la même approximation, les petites oscillations autour d’une position d’équilibre stable se font suivant une loi sinusoïdale. L’oscillateur est approximativement harmonique. En effet : \[K=\frac{d^2E_p}{dx^2}>0\quad\text{et}\quad E_p(0)~~\text{minimum}\]

2.4. Exemple : pendule composé

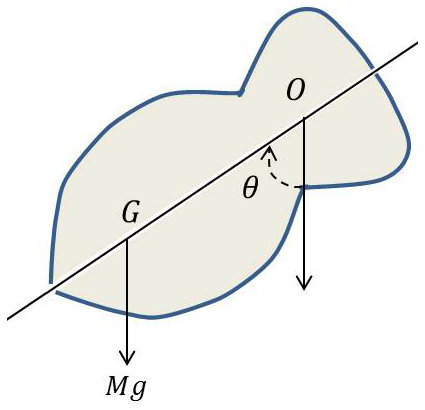Un pendule composé est un solide qui peut tourner autour d’un axe horizontal et qui est uniquement soumis à l’action de la pesanteur.

Soit \(O\) la trace de l’axe de rotation dans le plan de la figure, \(G\) le centre de gravité du solide \((OG = l)\) et \(\theta\) l’angle de \(OG\) avec la verticale descendante.

Le solide est soumis à un couple de rappel \(C\) dû aux forces de pesanteur : \[C=-M~g~l~\cos\theta\]

et à un couple d’inertie : \[I~\frac{d^2\theta}{dt^2}\]

\(I\) : moment d’inertie du solide par rapport à l’axe de rotation.

2.4.1. Calcul approché de la période

L"équation différentielle du mouvement est donc : \[I~\frac{d^2\theta}{dt^2}=-M~g~l~\sin\theta\]

En considérant l’approximation des petits angles : \[\frac{d^2\theta}{dt^2}+\frac{M~g~l}{I}~\theta=0\]

La solution générale est :

\[\begin{aligned} \theta&=\theta_0~\cos(\omega~t+\varphi)\\ \omega^2&=\frac{M~g~l}{I}\qquad;\qquad T=2~\pi~\sqrt{\frac{I}{M~g~l}}\end{aligned}\]

2.4.2. Calcul rigoureux de la période

On intègre cette fois l’équation : \[I~\frac{d^2\theta}{dt^2}+M~g~l~\sin\theta=0\]

que l’on peut transformer : \[I~\frac{d^2\theta}{dt^2}~\frac{d\theta}{dt}+M~g~l~\sin\theta~\frac{d\theta}{dt}=0\]

D’où l’intégrale des forces vives : \[I~\Big(\frac{d\theta}{dt}\Big)^2=2~M~g~l~(\cos\theta-\cos\theta_0)\]

\(\theta_0\) (élongation angulaire maximum) est l’amplitude des oscillations.

On en tire : \[dt=\sqrt{\frac{I}{M~g~l}}~\frac{d\theta}{\sqrt{2~(\cos\theta-\cos\theta_0)}}\]

En remarquant que : \[1-\cos\theta=2\sin^2~\frac{\theta}{2}\]

il vient : \[dt=\sqrt{\frac{I}{M~g~l}}~\frac{d\theta}{\sqrt{2~\Big(\sin^2\cfrac{\theta_0}{2}-\sin^2\cfrac{\theta}{2}\Big)}}\]

Posons : \[\sin\frac{\theta}{2}=\sin\frac{\theta_0}{2}~\sin\varphi\]

Et différencions : \[\frac{1}{2}~\cos\theta~d\theta=\sin\frac{\theta_0}{2}~\cos\varphi~d\varphi\quad\Rightarrow\quad d\theta=\frac{2~\cos\varphi~\sin\cfrac{\theta_0}{2}}{\cos\cfrac{\theta}{2}}~d\varphi\]

Par suite : \[dt=\sqrt{\frac{I}{M~g~l}}~\frac{d\varphi}{\sqrt{1-k^2~\sin^2\varphi}}\quad;\quad k^2=\sin^2\frac{\theta_0}{2}\]

Compte tenu du développement : \[(1-u)^{-1/2}=1+\frac{1}{2}~u+\frac{1}{2}~\frac{3}{4}~u^2+\dots\]

on peut écrire : \[dt=\sqrt{\frac{I}{M~g~l}}~\frac{d\varphi}{\sqrt{1-k^2~\sin^2\varphi}}= (1+\frac{1}{2}~k^2~\sin^2\varphi+\dots)~\sqrt{\frac{I}{M~g~l}}~d\varphi\]

En intégrant la série terme à terme, ce qui est légitime puisqu’elle est uniformément convergente pour \(|u|<1\) avec \(u\in\{\theta=0,~\theta=\theta_0\}\), soit avec la nouvelle variable \(u\in\{\varphi=0,\varphi=\pi/2\}\) et en tenant compte alors du fait que le temps varie de T/4, on a : \[\frac{T}{4}=\sqrt{\frac{I}{M~g~l}}~\Big\{\int_0^{\pi/2}d\varphi+\int_0^{\pi/2}\sin^2\varphi~d\varphi+\dots\Big\}\]

En se limitant aux premiers termes, et en remarquant que : \[\int_0^{\pi/2}\sin^2\varphi~d\varphi=\frac{\pi}{4}\]

il vient : \[T=2~\pi~\sqrt{\frac{I}{M~g~l}}~\Big(1+\frac{k^2}{4}+\dots\Big)\]

En le remplaçant par sa valeur \(\sin(\theta_0/2)\), et si \(\theta_0\) est suffisamment petit, on obtient en définitive : \[T=2~\pi~\sqrt{\frac{I}{M~g~l}}~\Big(1+\frac{\theta_0^2}{16}\Big)=T_0~\Big(1+\frac{\theta_0^2}{16}\Big)\]

\(T_0\) étant de fait la période des petites oscillations.

Le pendule est donc un oscillateur harmonique pour les petites amplitudes. Et si l’amplitude croît, la période dépend alors de l’amplitude.

3. Composition des oscillations sinusoïdales parallèles

On étudie la superposition de deux mouvements oscillatoires portés par le même axe, de la même variable, soit : \[x=x_1+x_2=a_1~\cos\omega_1~t+a_2~\cos(\omega_2~t+\varphi)\]

Nous supposerons dans un premier temps que les deux oscillations sont de même fréquence, c’est-à-dire que \(\omega_1=\omega_2=\omega\).

Après un calcul élémentaire, on obtient :

\[\begin{aligned} x&=A~\cos(\omega~t+\varphi')\\ A&=\sqrt{(a_1+a_2~\cos\varphi)^2+a_2^2~\sin^2\varphi}\quad;\quad tan\varphi'=\frac{a_2~\sin\varphi}{a_1+a_2~\cos\varphi}\end{aligned}\]

\[\begin{aligned} &\varphi=0 &&A=a_1+a_2 &&A_{max}\\ &\varphi=\pi &&A=a_1-a_2 &&A_{min}\\ &\varphi=\frac{\pi}{2} &&A=\sqrt{a_1^2+a_2^2} &&A_{quadrature}\end{aligned}\]

Énergie de la vibration résultante

Nous avions trouvé que l’énergie de l’oscillateur était proportionnelle au carré de l’amplitude : \[E=m~\frac{\omega^2~a^2}{2}\]

Dans le cas de la composition des deux vibrations :

• \(\varphi=0~:\quad A=(a_1+a_2)^2>a_1^2+a_2^2 \)

  L’énergie résultante est supérieure à la somme des énergies composantes.

• \(\varphi=\pi~:\quad A=(a_1-a_2)^2<a_1^2+a_2^2\)

  L’énergie résultante est inférieure à la somme des énergies composantes.

• \(\varphi=\cfrac{\pi}{2}~:\quad A=(a_1-a_2)^2=a_1^2+a_2^2\)

  L’énergie résultante est égale à la somme des énergies composantes.

4. Oscillations électriques sinusoïdales

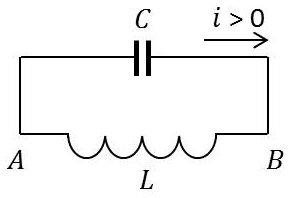L’analogue électrique de l’oscillateur mécanique sinusoïdal est constitué par le circuit oscillant obtenu en branchant borne à borne une inductance et une capacité.

\(V=V_A-V_B\) étant la d.d.p. aux bornes du condensateur : \[V_A-V_B=-L~\frac{di}{dt}\]

Soit \(q\) la charge du condensateur : \[V_A-V_B=V=\frac{q}{C}\]

On sait par ailleurs que : \[i=\frac{dq}{dt}\]

Il vient donc : \[L~\frac{d^2q}{dt^2}+\frac{q}{C}=0\qquad\text{analogue à}\qquad m~\frac{d^2x}{dt^2}+k~x=0\]

On peut noter les analogies suivantes :

• \(L\approx m\qquad\)    Masse ou inertie

• \(1/C\approx k\qquad\) Raideur du ressort

• \(q\approx x\qquad\)      Élongation

• \(i\approx v\qquad\)       Vitesse

Les lois de variation de la charge \(q\), de la tension \(V\) et de l’intensité \(i\) sont dès lors sinusoïdales.

L’énergie totale d’oscillation : \[E=\frac{L~i^2}{2}+\frac{q^2}{2~C}=cte\]

Nous verrons plus loin que ceci n’est possible que si l’énergie est constamment fournie au circuit oscillant. Un circuit oscillant réel présente en effet des pertes d’énergie ; l’une d’elle est due au rayonnement d’une onde hertzienne. Cette propriété est utilisée en TSF.

La transmission de paroles ou de musique s’obtient en modulant à fréquence musicale l’amplitude ou la fréquence de l’onde émise par le circuit, désignée sous le nom d’onde porteuse. Ces modulations seront étudiées de manière plus précise dans le chapitre réservé à la théorie du signal et des communications.

5. Composition de deux oscillations de périodes différentes

5.1. Oscillations de même amplitude

On postule que : \[x_1=a~\cos\omega_1~t\quad;\quad x_2=a~\cos(\omega_2~t+\varphi)\]

Tous calculs faits : \[x=x_1+x_2=2~a~\cos\Big\{\frac{\omega_1+\omega_2}{2}~t+\frac{\varphi}{2}\Big\}~\cos\Big\{\frac{\omega_1-\omega_2}{2}~t-\frac{\varphi}{2}\Big\}\]

Le mouvement résultant a donc lieu à la fréquence : \[\nu=\frac{\nu_1+\nu_2}{2}\]

Son amplitude est modulée à a fréquence : \[\nu=\frac{\nu_1-\nu_2}{2}\]

De plus, comme l’intensité est proportionnelle au carré de l’amplitude, \[4~a^2~\cos^2\Big\{\frac{\omega_1-\omega_2}{2}~t-\frac{\varphi}{2}\Big\}= 2~a^2~\big\{1+\cos\big[(\omega_1-\omega_2)~t-\varphi\big]\big\}\]

est modulée à la fréquence \(\nu_1-\nu_2\). C’est le phénomène des battements.

5.2. Oscillations d’amplitudes différentes

Quand les amplitudes des oscillations sont différentes, on a : \[x_1=a_1~\cos\omega_1~t\quad;\quad x_1=a_2~\cos(\omega_2~t+\varphi)\]

En notation complexe : \[z=a_1~\exp(\omega_1~t)+a_2~\exp(\omega_2~t+\varphi)\]

En représentation vectorielle, on peut dire que l’on ajoute au vecteur \(<a_1,~\omega_1~t>\) le vecteur \(<a_2,~\omega_2~t+\varphi>\). Le premier vecteur \(A\) tourne à la vitesse \(\omega_1\) suivant un cercle de rayon \(a_1\) et l’extrémité du vecteur résultant \(S\) tourne autour de \(A\) à la vitesse \(\omega=\omega_1-\omega_2\).

Étude du cas particulier \(a_2\ll a_1\)

En se reportant à une représentation graphique, cela équivaut à dire que la longueur du vecteur résultant \(OS\) peut être confondue avec la projection \(Os\) sur le vecteur \(AO\).

On obtient ainsi un mouvement modulé en amplitude : \[z\cong a_1~\Big\{1+\frac{a_2}{a_1}~\cos\big[(\omega_2-\omega_1)~t+\varphi\big]\Big\}~\cos\omega_1~t\]

Ce résultat est utilisé en TSF pour transformer à la réception les oscillations de fréquences très diverses reçues d’émetteurs différents en une oscillation de fréquence bien déterminée que le récepteur est capable d’amplifier correctement. C’est le principe de l’hétérodyne.