1. Introduction
Un mouvement oscillatoire indéfini peut être maintenu si un apport extérieur d’énergie vient compenser le travail résistant inévitable des forces de frottement. Deux cas principaux peuvent alors se présenter :
-
L’appoint d’énergie est fourni par application à l’oscillateur d’une force extérieure périodique, de période imposée par l’oscillateur. On se trouve alors en présence d’oscillations forcées, de période égale à celle de la force agissante.
-
L’oscillateur déclenche, à chacune de ses oscillations, un mécanisme extérieur qui leur fournit alors une certaine quantité d’énergie. On se trouve alors en présence d’oscillations entretenues, dont la période est principalement imposée par l’oscillateur lui-même (elle est toutefois un peu modifiée par le dispositif d’entretien).
Nous étudierons tout d’abord les oscillations forcées et considèrerons en premier lieu le cas le plus simple, celui où la force appliquée à l’oscillateur varie de manière sinusoïdale au cours du temps.
2. Oscillations forcées. Action sinusoïdale
Prenons le cas de l’oscillateur soumis à une force de frottement liquide. Nous obtiendrons une équation de la forme : \[m~\frac{d^2x}{dt^2}+f~\frac{dx}{dt}+k~x=F~\cos\Omega~t\]
Posons : \[\frac{f}{m}=2~\alpha~\omega_0\quad;\quad \omega_0^2=\frac{k}{m}\]
L’équation s’écrit : \[\frac{d^2x}{dt^2}+2~\alpha~\omega_0~\frac{dx}{dt}+\omega_0^2~x=\frac{F}{m}~\cos\Omega~t\]
La solution générale est la somme d’une intégrale particulière de l’équation complète et de la solution générale de l’équation sans second membre. On trouvera donc : \[x=a\exp(-\alpha~\omega_0~t)~\cos(\omega~t+\varphi)+f(t)\]
Le premier terme du second membre voit son amplitude décroître exponentiellement avec le temps et il disparaît progressivement. Il ne reste plus au bout d’un certain temps que le mouvement qui correspond à la solution particulière. Ce mouvement caractérise le régime permanent.
2.1. Étude du régime permanent
Cherchons une intégrale particulière de l’équation avec second membre : \[\frac{d^2x}{dt^2}+2~\alpha~\omega_0~\frac{dx}{dt}+\omega_0^2~x=\frac{F}{m}~\cos\Omega~t\]
Passons aux variables complexes en introduisant l’équation conjuguée : \[\frac{d^2y}{dt^2}+2~\alpha~\omega_0~\frac{dy}{dt}+\omega_0^2~y=\frac{F}{m}~\sin\Omega~t\]
Considérons la fonction complexe \(z=x+jy\) qui satisfait alors à l’équation : \[\frac{d^2z}{dt^2}+2~\alpha~\omega_0~\frac{dz}{dt}+\omega_0^2z=\frac{F}{m}~\cos\Omega~t\]
La partie réelle correspond à \(x\) et la partie imaginaire à \(y\).
Cherchons une solution de la forme : \[z=\chi~\exp(j~\Omega~t)\]
On a donc : \[\chi~(-\Omega^2)+2~j~\Omega~\omega_0~\alpha+\omega_0^2)=\frac{F}{m}\qquad\qquad\chi\in\mathbb{C}\]
Par suite : \[\chi=\frac{F}{m~(\omega_0^2-\Omega^2+~j~\Omega~\omega_0~\alpha)}\]
Cette quantité \(\chi\) est désignée sous le nom d’amplitude complexe de l’oscillation. Son argument représente l’avance de phase de l’oscillateur sur la force appliquée et son module \(X\) l’amplitude de l’oscillation.
La différence de phase entre l’oscillateur et la force appliquée est telle que : \[\tan\varphi=-\frac{2~\Omega~\omega_0~\alpha}{\omega_0^2-\Omega^2}\]
2.2. Vitesse de l’oscillateur
Considérons la relation : \[\frac{dz}{dt}=\chi~j~\Omega~\exp(j~\Omega~t)=v~\exp(j~\Omega~t)\]
\[\begin{aligned} &v &&\text{amplitude complexe de la vitesse} \\ &V=|v| &&\text{amplitude réelle} \\ &\Psi=\arg(v) &&\text{avance de phase}\end{aligned}\]
On a donc : \[v=V~\exp\{j~(\Omega~t+\Psi)\}\]
L’amplitude complexe de la vitesse se déduit de celle de l’élongation par la relation : \[v=~j\Omega~\chi=j\Omega~\frac{F}{m~(\omega_0^2-\Omega^2+2~j~\Omega~\omega_0~\alpha)}\]
2.3. Impédance de l’oscillateur
Par définition, l’impédance de l’oscillateur est égale au quotient de l’amplitude complexe de la force par l’amplitude complexe de la vitesse : \[Z=\frac{F}{v}\qquad\qquad Z\in\mathbb{C}\]
Le module de l’impédance est : \[z=|Z|=\frac{F}{V}\]
Remarquons en effet que l’amplitude complexe de la force est ici un nombre réel puisque nous avons choisi sa phase comme origine des phases en l’écrivant sous la forme \(F~\cos\Omega~t\).
L’argument de l’impédance \(\arg(Z)=\arg(F)-\arg(v)\) représente l’avance de phase de la force sur la vitesse.
En fait : \[\arg(F)=0\quad\Rightarrow\quad \arg(z)=-\arg(v)\]
L’expression de l’impédance complexe est : \[Z=\frac{F}{v}=-\frac{m~(\omega_0^2-\Omega^2+2~j~\Omega~\omega_0~\alpha)}{j~\Omega}\]
Tous calculs faits : \[Z=f+j~\frac{m}{\Omega}~(\Omega^2-\omega_0^2) =f+j~\Big(m~\Omega-\frac{k}{\Omega}\Big)\]
L’impédance réelle (rapport des amplitudes réelles de la force et de la vitesse) est : \[Z=\sqrt{f^2+j~\Big(m~\Omega-\frac{k}{\Omega}\Big)^2}\]
Diverses formes de l’impédance
On peut écrire : \[Z=m~\omega_0~\Big\{2~\alpha+j~\Big(\frac{\Omega}{\omega_0}-\frac{\omega_0}{\Omega}\Big)\Big\}\]
En posant \(i=\Omega/\omega_0\) (intervalle entre la pulsation propre à l’oscillateur et la pulsation de la force) :
\[\begin{aligned} &Z=m~\omega_0~\Big\{2~\alpha+j~\Big(i-\frac{1}{i}\Big)\Big\} &&\text{ou}\qquad Z=f+j~m~\omega_0~\Big(i-\frac{1}{i}\Big)\\ &Z=\sqrt{f^2+\Big(m~\Omega-\frac{k}{\Omega}\Big)^2} &&\text{ou}\qquad Z=\sqrt{f^2+m^2~\omega_0^2~\Big(i-\frac{1}{i}\Big)^2}\end{aligned}\]
Variation du module de l’impédance en fonction de \(i\)
On part de l’expression : \[\sqrt{f^2+m^2~\omega_0^2~\Big(i-\frac{1}{i}\Big)^2}\]
Discussion
-
\(i\rightarrow 0~;~~~Z\rightarrow\infty~;~V\rightarrow 0\) : l’oscillateur se comporte comme un ressort.
-
\(f\rightarrow\infty~;~Z\rightarrow\infty~;~V\rightarrow 0\) : l’oscillateur se comporte comme une masse inerte.
-
\(i=1~;~~~Z=Z_{min}=f\) : l’oscillateur est attaqué dans sa pulsation propre : il y a résonance. L’oscillateur se comporte alors comme s’il se réduisait à la seule résistance visqueuse.
2.4. Étude détaillée du mouvement permanent
Variation de \(\Psi\)
\(\Psi\) est l’avance de phase de la vitesse par rapport à la force.
D’après ce qui précède : \[\Psi=-\arg(Z)=-\arg\Big\{m~\omega_0~\Big[2~\alpha+j~\Big(i-\frac{1}{i}\Big)\Big]\Big\}\]
Tous calculs faits : \[\tan\Psi=\frac{1-1/i}{\alpha}\quad;\quad \sin\Psi=\frac{1-1/i}{\sqrt{4~\alpha^2+(1-1/i)^2}}\quad;\quad \cos\Psi=\frac{2~\alpha}{\sqrt{4~\alpha^2+(1-1/i)^2}}\]
Discussion
-
\(i\rightarrow 0~;~~~\sin\Psi\rightarrow 1~;~\Psi\rightarrow\pi/2\) : vitesse en quadrature avance sur la force appliquée
-
\(i\rightarrow\infty~;~\sin\Psi\rightarrow 0~;~\Psi\rightarrow-\pi/2\) : vitesse en quadrature retard sur la force appliquée
-
\(i=0~;~~~~\sin\Psi=0~;~\cos\Psi=1~;~\Psi=0\) : vitesse et force appliquée en phase
Variation de \(\varphi\)
\(\varphi\) est la différence de phase entre l’élongation et la force appliquée.
Il suffit par ailleurs de remarquer que \(\Psi=\varphi+\pi/2\).
Discussion
-
\(i\rightarrow 0~;~~~\Psi\rightarrow\pi/2~;~\varphi\rightarrow 0\) : mouvement en phase sur la la force
-
\(i\rightarrow\infty~;~\Psi\rightarrow\pi/2~;~\varphi\rightarrow-\pi\) : mouvement en opposition de phase sur la la force
-
\(i=1~;~~~~\Psi=0~;~\varphi=-\pi/2\) : mouvement quadrature retard avec la force
Étude du module X de l’élongation
On rappelle que : \[X=\frac{V}{\Omega}\quad;\quad V=\frac{F}{Z}\quad;\quad X=\frac{F}{\Omega~Z}\]
Ce qui donne : \[X=\frac{F}{m~\Omega~\omega_0~\sqrt{4~\alpha^2+(i-1/i)^2}}\]
\(X\) sera maximum lorsque le carré du dénominateur sera minimum, c’est-à-dire lorsque la quantité : \[y=\Omega^2~\{4~\alpha^2+(i-1/i)^2\}\]
sera minimale. Par ailleurs, on peut écrire : \[y=\omega_0^2~i^2~\{4~\alpha^2+(i-1/i)^2\}=\omega_0^2~\{4~\alpha^2~i^2+(i^2-1)^2\}\]
En dérivant l’expression : \[\frac{d}{di}\Big(\frac{y}{\omega_0^2}\Big)=8~\alpha^2~i+4~i~(i^2-1)=4~i~\{i^2-(1-2~\alpha^2)\}\]
L’expression s’annule pour : \[i=0\quad;\quad i=\sqrt{1-2~\alpha^2}\]
L’autre solution n’est pas acceptable, car \(i\) réel et positif.
La deuxième solution nécessite : \[1-2~\alpha^2>0;\quad\text{soit :}\quad\alpha<\frac{1}{\sqrt{2}}\]
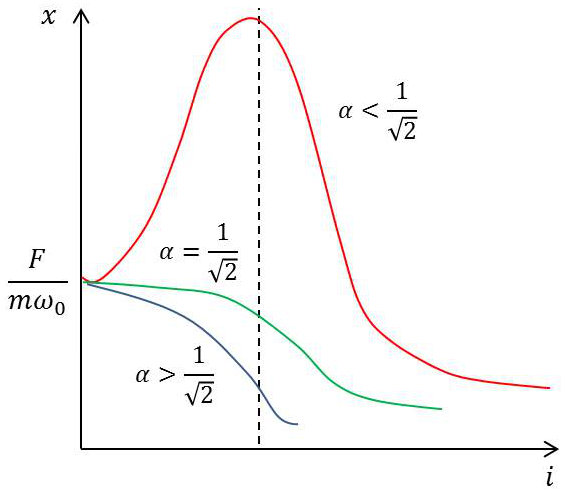 \(1/\sqrt{2}<\alpha<1\) :
\(1/\sqrt{2}<\alpha<1\) :
– une racine : \(i=0\quad(y_{min},~X_{max})\)
\(\alpha<1/\sqrt{2}\) :
– première racine : \(i=0\quad(y_{max},~X_{min})\)
– deuxième racine : \(i=\sqrt{1-2~\alpha^2}\)
\(\alpha=1/\sqrt{2}\) :
– trois racines confondues : \(i=0\) : méplat
Lieu des maximums
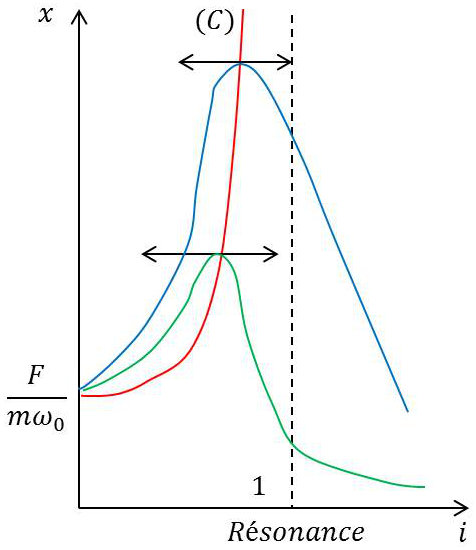
Lorsque \(\alpha<1/\sqrt{2}\), pour \(i=i_m\), on obtient : \[X=\frac{F}{m~\omega_0^2}~\frac{1}{\sqrt{4~\alpha^2~i_m^2+(1-i_m^2)^2}}\]
 Or, \(i_m=\sqrt{1-2~\alpha^2}\), c’est-à-dire que l’on obtient, tous calculs faits : \[X=\frac{F}{m~\omega_0^2}~\frac{1}{\sqrt{1-i_m^4}}\]
Or, \(i_m=\sqrt{1-2~\alpha^2}\), c’est-à-dire que l’on obtient, tous calculs faits : \[X=\frac{F}{m~\omega_0^2}~\frac{1}{\sqrt{1-i_m^4}}\]
Premier cas : \[i_m\rightarrow 0\qquad X\rightarrow\frac{F}{m~\omega_0^2}\]
Deuxième cas : \[i_m\rightarrow 1\qquad X\rightarrow\infty\]
ce qui correspond à : \[\sqrt{1-2~\alpha^2}\rightarrow 1\qquad\alpha\rightarrow 0\]
D’où la courbe rouge ci-contre, lieu des maximums.
2.5. Représentation graphique de l’impédance complexe
On peut écrire (dans le plan complexe) :
\[\begin{aligned} &Z=Z_x+jZ_y=m\omega_0~\{2~\alpha+j~(i-1/i)\}\\ &Z_x=f=2~\alpha~m~\omega_0\quad;\quad Z_y=(i-1/i)~m~\omega_0\end{aligned}\]
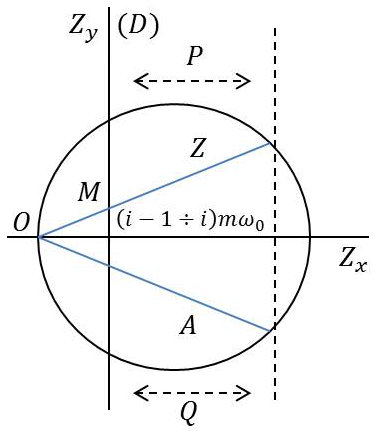 Lorsque \(i\) varie, le point \(M\) se déplace sur la droite \((D)\).
Lorsque \(i\) varie, le point \(M\) se déplace sur la droite \((D)\).
Introduisons l’admittance complexe \(A\) : \[A=\frac{1}{Z}\quad\Rightarrow\quad v=A~F\quad\text{(v est proportionnel à A)}\]
Lorsque \(i\) varie, l’extrémité de \(A\) se déplace sur le cercle inverse de \((D\)) dans l’inversion \((O,~1)\). D’où la construction de \(A\).
On peut retrouver, à l’aide du graphique, les résultats déjà obtenus.
-
\(i\rightarrow 0~;~(i-1/i)\rightarrow -\infty~;~|Z|\rightarrow\infty \) : \(M\) s’éloigne indéfiniment vers le bas
-
\(\arg(A)\rightarrow \pi/2~;~|A|\rightarrow 0\) : pour \(i\) faible, \(v\) en quadrature avance sur la force
-
\(i\rightarrow\infty~;~(i-1/i)\rightarrow \infty~;~|Z|\rightarrow\infty \) : \(M\) s’éloigne indéfiniment vers le haut
-
\(\arg(A)\rightarrow -\pi/2~;~|A|\rightarrow 0\) : pour \(i\) grand, \(v\) en quadrature retard sur la force
-
\(i=1~;~(i-1/i)=0\) : \(A\) maximum en module (résonance) : \(\arg(A)=0~;~A=1/f\)
Remarque
Les sommets du cercle, \(P\) et \(Q\), points à tangente horizontale, sont obtenus lorsque : \[i=\frac{1}{i}=\pm 2~\alpha\quad;\quad |A|_{\text{P ou Q}}=\frac{|A|_{max}}{\sqrt{2}}\]
Les valeurs de \(i\) donnant ce résultat sont racines de l’une des équations : \[i^2\pm 2~\alpha~i-1=0\]
Ce qui donne :
\[\begin{aligned} &i=\pm~\alpha-\sqrt{\alpha^2-1}\qquad\text{à rejeter car~}~i>0\\ &i=\pm~\alpha+\sqrt{\alpha^2-1}\end{aligned}\]
Les deux valeurs de \(i\) cherchées sont donc : \[\{i_1,~i_2\}=\pm~\alpha+\sqrt{\alpha^2-1}\]
Remarquons que : \[i_1~i_2=(\sqrt{\alpha^2+1}+\alpha)~(\sqrt{\alpha^2+1}-\alpha)=1\]
Pour un amortissement très faible (\(\alpha\ll 1\)) : \[i_1~\cong~+\alpha\quad;\quad i_2~\cong~1-\alpha\]
et dans tous les cas : \[i_1-i_2=2~\alpha\]
La quantité \(1/2~\alpha\) est désignée sous le nom d’acuité de résonance.
Plus \(2~\alpha\) est petit, plus le maximum est aigu. \[i_1-i_2=\frac{\Omega_1}{\omega_0}-\frac{\Omega_2}{\omega_0}=2~\alpha\]
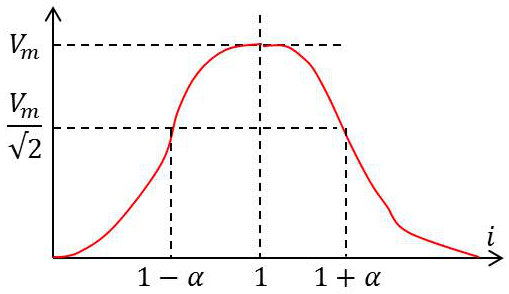 L’intervalle de pulsations \((i_1-i_2)~\omega_0\) constitue la bande passante de l’oscillateur.
L’intervalle de pulsations \((i_1-i_2)~\omega_0\) constitue la bande passante de l’oscillateur.
On remarquera que : \[\Omega\in(i_1-i_2)~\omega_0~~\Rightarrow~~\frac{V_m}{\sqrt{2}}<(i_1-i_2)~\omega_0<V<V_m\]
Plus \(2~\alpha\) est petit et plus la variation de la phase de la vitesse est rapide à la traversée de la résonance. Il en est de même pour la phase du mouvement \(\varphi=\Psi-\pi/2\).
En effet, aux bords de la bande passante, \(\Psi\) est déjà égal à \(\pm\pi/4\) (ce qui est évident sur la représentation géométrique de l’impédance : sommets du cercle).
2.6. Travail dépensé par l’oscillateur pendant une période
Calculons le travail nécessaire pour entretenir l’oscillateur pendant une période. Pour un déplacement \(dx\) de l’oscillateur, le travail élémentaire de la force appliquée est : \[dW=F~\cos\Omega~t~dx=F~\cos\Omega~t~v~dt\]
Pendant une période le travail dépensé est : \[W=\int_0^T F~\cos\Omega~t~v~dt\quad;\quad v=\frac{F}{Z}~\cos(\Omega~t+\Psi)\]
On a donc :
\[\begin{aligned} &W=\frac{F^2}{Z}\int_0^T \cos\Omega~t~\cos(\Omega~t+\Psi)~dt\\ &W=\frac{F^2}{Z}\int_0^T \frac{1}{2}~\{\cos(2~\Omega~t+\Psi)+\cos\Psi\}~dt=\frac{F^2}{Z}~\frac{T}{2}~\cos\Psi\end{aligned}\]
La puissance moyenne dépensée est donc : \[P=\frac{W}{T}=\frac{F^2}{2~Z}~\cos\Psi\]
D’autre part : \[\cos\Psi=\frac{2~\alpha}{\sqrt{4~\alpha^2+(i-1/i)^2}}=\frac{2~\alpha}{Z/\omega_0~m}=\frac{f}{Z}\]
On a donc : \[\overline{P}=\frac{f}{2}~\Big(\frac{F}{Z}\Big)^2=\frac{f}{2}~V^2\]
La puissance dissipée est maximale à la résonance : \[i=1\quad\Rightarrow\quad Z=f\quad;\quad P_m=\frac{f}{2}~\Big(\frac{F}{Z}\Big)=\frac{F^2}{2~f}=\frac{f}{2}~V_{max}^2\]
Remarque
Calculons le travail dissipé en frottements :
\[\begin{aligned} &dW'=f~\frac{dx}{dt}~dt=f~v^2~dt\\ &\int_0^T dW'=f\int_0^T v^2~dt=T~f~v^2=T~f~\frac{V^2}{2}\end{aligned}\]
Soit une puissance dissipée en frottements : \[\overline{P'}=\frac{1}{T}\int_0^T dW'=f~\frac{V^2}{2}\]
On retrouve bien la même expression.
2.7. Force réelle agissant sur la masse m
La force réelle agissant sur la masse \(m\) est \(m~d^2x/dt^2\) et son amplitude complexe est donc : \[F'=j~m~\Omega~v\quad;\quad |F'|=m~\Omega~v=m~\frac{\Omega}{Z}~f\]
Par ailleurs : \[Z=\omega_0~m~\sqrt{4\alpha^2+(i-1/i)^2}\]
On a donc : \[|F'|=F~\frac{i}{\sqrt{4\alpha^2+(i-1/i)^2}}\]
Le radical est minimum pour \(i=1\). Ceci n’entraine pas toutefois le maximum de \(|F'|\), car \(i\) figure au numérateur. Le maximum de \(|F'|\) a donc lieu pour \(i\) légèrement supérieur à 1.
En définitive, les maximums se répartissent comme suit :
-
Amplitude \(x\) pour \(i<1\)
-
Frottement \(dx/dt\) pour \(i=1\)
-
Force d’inertie \(m~d^2x/dt^2\) pour \(i>1\)
À la résonance, \(|F'|=F/2~\alpha\), la force réelle agissant sur la masse \(m\) est égale au produit de la force appliquée par l’acuité de la résonance.
2.8. Étude du régime transitoire
On désigne sous le nom de régime transitoire le mouvement compliqué de l’oscillateur qui résulte, immédiatement après l’application de la force \(F~\cos\Omega~t\), de la superposition du mouvement amorti solution de l’équation sans second membre et du mouvement permanent.
On observe des battements de moins en moins marqués à mesure que disparaît le mouvement transitoire, comme cela résulte de la solution générale : \[x=a~\exp(-\omega_0~t)~\sin(\omega~t+\varphi_1)+X~\cos(\Omega~t+\varphi)\]
Cas de la résonance
On suppose que : \[\alpha\ll 1\quad;\quad \omega\cong\omega_0\]
À la résonance : \[\Omega~=~\omega~\cong~\omega_0\]
La solution devient :
\[\begin{aligned} x&=a~\exp(-\omega_0~t)~\sin(\omega~t+\varphi_1)~X~\sin(\Omega~t)\\ \frac{dx}{dt}&=a~\exp(-\omega_0~t)~\{-\alpha~\Omega~\sin(\omega~t+\varphi_1)+\Omega~\cos(\omega~t+\varphi_1)\}-X~\Omega~\cos\Omega~t\end{aligned}\]
Supposons l’oscillateur au repos en \(O\) lors de l’application de la force : \[\text{Si}~~t=0,\quad \left\{ \begin{aligned} &x=0~; &&x=a\sin\varphi_1=0~; &&\varphi_1=0\\ &\frac{dx}{dt}=0~; &&a~\Omega-X~\Omega=0~; &&a=X \end{aligned} \right.\]
D’où la solution (approximative pour \(\alpha\ll1\)) : \[x=X~\{1-\exp(-\alpha~\Omega~t)~\sin\Omega~t\}\]
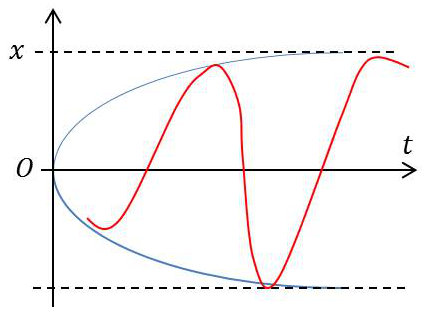 L’amplitude d’oscillation tend progressivement vers l’amplitude du régime X.
L’amplitude d’oscillation tend progressivement vers l’amplitude du régime X.
On aura l’amplitude \(X/2\) lorsque : \[1-\exp(-\alpha~\omega_0~t)=\frac{1}{2}\quad\Rightarrow\quad t=\frac{1}{\alpha~\omega_0}~\ln 2=\theta\]
n oscillations auront été effectuées, avec \(n=\theta/T\) :
\[\begin{aligned} &n=\frac{\ln 2}{\alpha~\omega_0~T}=\frac{\ln 2}{2~\pi~\alpha}=\frac{1}{2~\alpha}~\frac{\ln 2}{\pi}=\frac{1}{4}~\frac{1}{2~\alpha}\\ &(\text{pour}~\alpha=\frac{1}{100},~~n~\cong~1,25)\end{aligned}\]
2.9. Analogie électrique
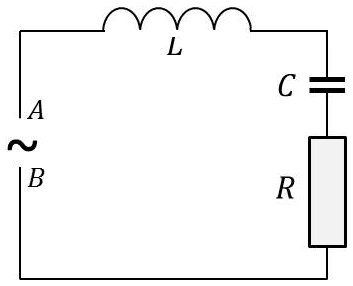 La tension sinusoïdale appliquée aux bornes \(A\) et \(B\) du circuit \(L,~R,~C\) est : \[V_A-V_B=V_0~\exp(j~\Omega~t)=e=E~\exp(j~\Omega~t)\]
La tension sinusoïdale appliquée aux bornes \(A\) et \(B\) du circuit \(L,~R,~C\) est : \[V_A-V_B=V_0~\exp(j~\Omega~t)=e=E~\exp(j~\Omega~t)\]
La tension aux bornes du condensateur varie selon la loi : \[x=a~\exp(-\omega_0~t)~\sin(\omega~t+\varphi_1)+X~\cos(\Omega~t+\varphi)\]
En effet : \[\frac{d^2q}{dt^2}+\frac{R}{L}~\frac{dq}{dt}+\frac{q}{L~C}=\frac{E}{L}~\exp(j~\Omega~t)\quad;\quad q=C~V\]
Poursuivant les analogies :
\[\begin{aligned} &\frac{dq}{dt}=\mathcal{I}~\exp(j~\Omega~t)\quad;\quad\mathcal{I}=\frac{E}{Z}\quad;\quad |\mathcal{I}|=I\\ &Z=R+j~(L~\Omega-\frac{1}{C~\Omega})=L~\omega_0~\Big\{2~\alpha+j~\Big(i-\frac{1}{i}\Big)\Big\}\\ &|Z|=\sqrt{R^2+(L~\Omega-\frac{1}{C~\Omega})^2}\end{aligned}\]
Puissance moyenne dissipée dans le circuit
\[\begin{aligned} &\overline{P}=\frac{E^2}{2~Z}~\cos\Psi=\frac{E~I}{2}~\cos\Psi\\ &\cos\Psi=\frac{R}{Z}\qquad\text{car :}\quad R=f\end{aligned}\]
On a donc : \[\overline{P}=\frac{R~I^2}{2}\]
Tension aux bornes du condensateur à la résonance \[V=V_m=\frac{I_m}{C~\omega_0}=\frac{E}{R~C~\omega_0}=E~\frac{L~\omega_0}{R}=\frac{E}{2~\alpha}\]
L’acuité de résonance \(1/2~\alpha\) est pour cette raison désignée souvent sous le nom de surtension du circuit.

