1. Modèle de Bohr
Par analogie avec le modèle planétaire de Kepler, Bohr émit l’hypothèse d’orbites circulaires (un seul paramètre) avec les postulats suivants :
 Dans ce mouvement circulaire : \[m~a^2~\omega~=~\frac{n~h}{2\pi}\]
Dans ce mouvement circulaire : \[m~a^2~\omega~=~\frac{n~h}{2\pi}\]
où : \[\omega=\frac{n~h}{2\pi}~\frac{1}{m~a^2}\quad;\quad n~=~1,~2,~3...\]
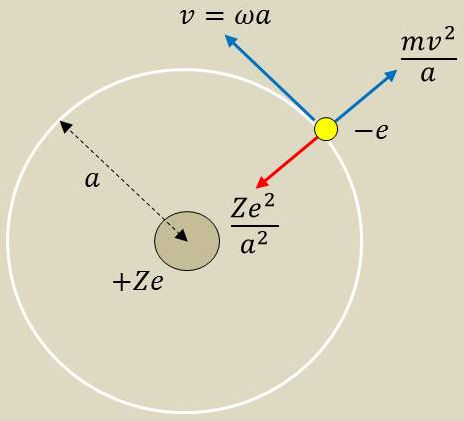
L’hypothèse de Bohr conservait les lois de la mécanique classique : sur son orbite privilégiée (il ne rayonne pas), l’électron trouve son équilibre entre deux forces :
-
l’attraction électrostatique : \(\cfrac{Ze^2}{a^2}\) (charge positive \(Ze\) du noyau) ;
-
la force d’inertie : \(\cfrac{m~v^2}{a}\) .
On a donc : \[v=\omega~a\qquad\Rightarrow\qquad\frac{Z~e^2}{a^2}=m~\omega^2~a\]
et l’élimination de \(\omega\) conduit à : \[a=\frac{h^2}{4\pi^2}~\frac{n^2}{m~Z~e^2}=\frac{n^2}{Z}~(0,528\times 10^{-8}~\rm m)\]
L’énergie cinétique de l’électron est alors : \[E_c=\frac{1}{2}~m~a^2~\omega^2\]
et son énergie totale : \[E=E_c+E_p\qquad(E_p~:~\text{énergie potentielle})\]
D’où l’expression de l’énergie correspondant à une orbite caractérisée par \(n\) : \[E_n~=~-~\frac{2\pi^2~m~Z^2~e^4}{n^2~h^2}\]
L’énergie est proportionnelle à \(Z^2/n^2\) : elle diminue vers les couches externes.
Jusqu’à présent, un seul nombre \(n\) caractérise l’électron dans son atome : \[\begin{matrix} &n=1& &K& &E_K\\ &n=2& &L& &E_L\\ &n=3& &M& &E_M \end{matrix}\]
2. Modèle de Sommerfeld
Le modèle de Bohr ne prend pas en compte deux éléments :
-
orbite réelle elliptique donc non circulaire ;
-
noyau non ponctuel, en mouvement par rapport à un centre de gravité.
Moyennant deux opérations :
-
quantification des orbites elliptiques ;
-
introduction de la mécanique relativiste,
Sommerfeld est parvenu à une expression plus complexe : \[E_{n,l}~=~E_n~\Big\{1+\frac{\alpha^2~Z^2}{n^2}~\Big(\frac{n}{l+1}-\frac{3}{4}\Big)\Big\}\]
-
\(E_n\) : énergie de Bohr
-
\(\alpha\) : constante de structure fine
Avec, cette fois, la présence de deux nombres quantiques : \(n\) et \(l~\in~\{~0,~1,~2,~...,~n-1~\}\).
On passe des 3 niveaux d’énergie de Bohr (\(K,~L,~M\)) à un plus grand nombre de niveaux Sommerfeld, suite à l’introduction des nombres quantiques \(n\) et \(l\). \[\left\{ \begin{matrix} &K\\ &L\\ &M \end{matrix} \right. \qquad \Rightarrow \qquad \left\{ \begin{matrix} &K\\ &L_0&&L_1\\ &M_0&&M_1&&M_2 \end{matrix} \right.\]
Cependant, l’expérience allait permettre de constater l’existence :
-
d’une structure fine de 3 raies au lieu de 2 pour le niveau \(L\) ;
-
d’une structure fine de 5 raies au lieu de 3 pour le niveau \(M\).
Pour élargir la théorie, Sommerfeld suggéra alors l’introduction d’un nombre quantique supplémentaire \(j\) qu’il appela nombre quantique interne, sans être en mesure pour autant d’apporter plus de précisions.
La théorie restait incomplète, ce que mit en évidence l’action d’un champ magnétique sur les raies spectrales émises par les atomes (effet Zeeman).
3. Moment cinétique, moment magnétique et spin
3.1. Moment cinétique (ou moment angulaire orbital)
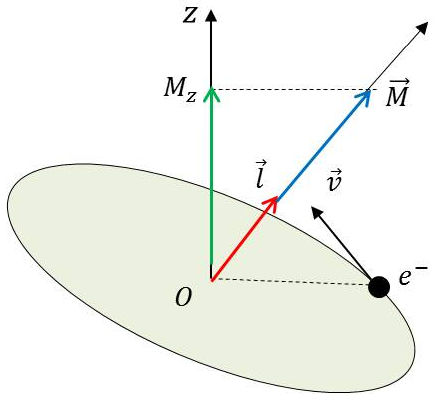 Le moment de la quantité de mouvement de l’électron par rapport au noyau : \[\vec{p}~=~m~\vec{v}\]
Le moment de la quantité de mouvement de l’électron par rapport au noyau : \[\vec{p}~=~m~\vec{v}\]
La quantité vectorielle \(\overrightarrow{M}\) est orientée perpendiculairement au plan défini par le vecteur \(\vec{p}\) et le noyau de l’atome pris comme origine.
Au vecteur \(\overrightarrow{M}\), correspond un vecteur \(\vec{l}\) à (\(2l+1\)), orientations discontinues dans l’espace : \[\overrightarrow{M}~=~\frac{h}{2\pi}~\overrightarrow{l}\]
Les orientations de \(\overrightarrow{l}\) sont définies par rapport à un axe fixe sans signification physique particulière appelé axe de quantification \(Oz\).
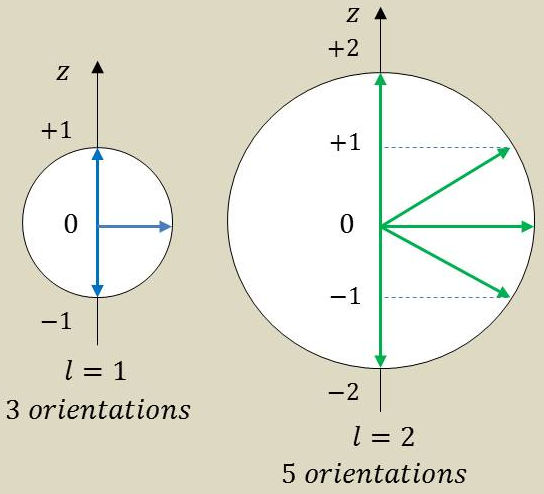 \(M_z\), projection \(\overrightarrow{M}\) sur cet axe, est également quantifiée.
\(M_z\), projection \(\overrightarrow{M}\) sur cet axe, est également quantifiée.
Ainsi, à l’état \(l=1\) de l’électron correspondent 3 orientations possibles de \(\overrightarrow{M}\) et 5 orientations pour \(l=2\), mais ces états sont caractérisés par la même énergie \(E_{n,l}\) qui ne dépend que des nombres quantiques \(n\) et \(l\).
Nous allons voir à présent que si l’atome est placé dans un champ magnétique, les trois états (\(l=1\)) et les cinq états (\(l=2\)) possèderont alors des énergies différentes, ce qui conduit à une séparation des niveaux. C’est l’effet Zeeman.
3.2. Moment magnétique
La gravitation des électrons autour du noyau est équivalente à des courants électriques. L’atome est alors assimilable à un petit aimant que l’on peut alors caractériser par son moment magnétique \(\overrightarrow{\mathcal{M}}\). Dans le cas d’un seul électron : \[\overrightarrow{\mathcal{M}}~=~\frac{e}{2c}~a~\vec{v}\]
Le moment cinétique d’un tel électron étant \(\overrightarrow{M}~=~m~a~\vec{v}\), on a les relations : \[\overrightarrow{\mathcal{M}}~=\frac{e}{2~m~c}~\overrightarrow{M}\qquad\Rightarrow\qquad \mathcal{M}_z~=~\frac{e}{2~m~c}~M_z\]
Dans un champ magnétique extérieur \(\overrightarrow{\mathcal{H}}\), l’électron aura une énergie additionnelle : \[\Delta E~=~\mathcal{M}_z~\mathcal{H}~=~\frac{e}{2~m~c}~M_z~\mathcal{H}\]
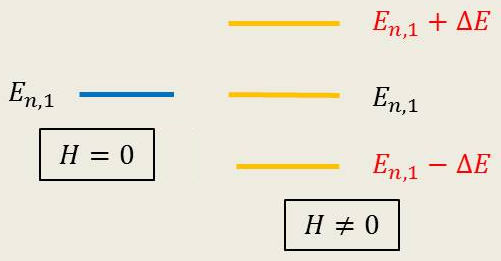 Soit encore : \[\Delta E~=~\frac{e}{2~m~c}~\frac{h}{2\pi}~\mathcal{H}\]
Soit encore : \[\Delta E~=~\frac{e}{2~m~c}~\frac{h}{2\pi}~\mathcal{H}\]
Une représentation simplifiée de la distribution de l’énergie(voir figure ci-contre).
Il s’agit là d’un effet Zeeman normal.
3.3. Moment angulaire de rotation ou spin
L’atome n’est plus non ponctuel, mais assimilable à une sphère minuscule dont le rayon est de l’ordre de dimension du noyau : il tourne sur lui-même à la manière d’une toupie. Sa description a néanmoins dû être complétée par un quatrième paramètre, le spin ou mouvement angulaire de rotation, également quantifié : \[\overrightarrow{M}_{rot}~=~\frac{h}{2\pi}~\vec{s}\]
La valeur de \(s\) a été choisie pour rendre compte de l’expérience : \[s~=~\frac{1}{2}~~\text{en unité}~~\frac{h}{2\pi}\]
Cette rotation entraînait à son tour l’existence d’un moment magnétique intrinsèque : \[\vec{\mu}~=\frac{e}{2~m~c}~\overrightarrow{M}_{rot}\qquad\Rightarrow\qquad\mu_z~=~\frac{e}{2~m~c}~M_{z~rot}\]
L’électron devenait assimilable à un petit aimant de forme sphérique en rotation autour du diamètre défini par la ligne des pôles.
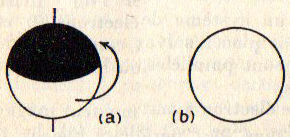 La figure révèle deux aspects physiques importants :
La figure révèle deux aspects physiques importants :
-
image de l’électron avec spin
-
image de l’électron sans spin
Remarques
 L’introduction du spin rend compte de l’effet Zeeman anormal.
L’introduction du spin rend compte de l’effet Zeeman anormal.
Elle éclairait de plus d’un jour nouveau l’introduction par Sommerfeld du nombre quantique interne \(j\).
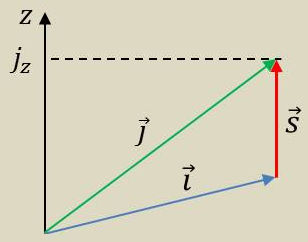
Cette grandeur \(\vec{j}\) pouvait s’interpréter comme la résultante des moments cinétiques \(\vec{l}\) et \(\vec{s}\).
\(\vec{j}\) représente ainsi un moment angulaire total.
4. Règles pour le cortège électronique
4.1. Règles de base
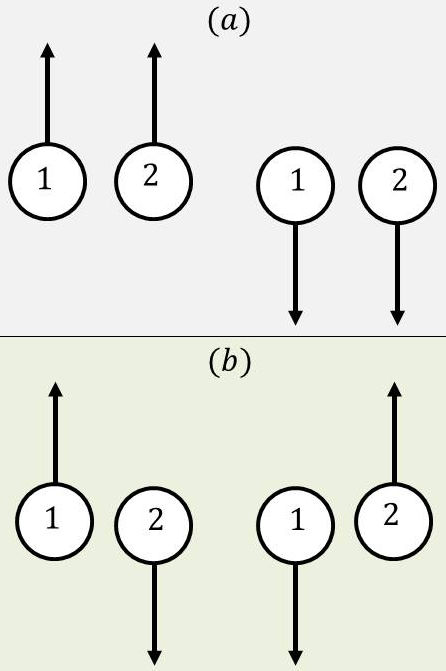 Si l’on envisage par exemple un système de deux électrons (1) et (2), quatre configurations sont envisageables :
Si l’on envisage par exemple un système de deux électrons (1) et (2), quatre configurations sont envisageables :
-
deux où les spins sont parallèles (a) ;
-
deux où les spins sont anti-parallèles (b).
Chaque électron a un moment magnétique \(\mu\).
Dans les configurations (a), les spins étant parallèles, les moments magnétiques additionnent leurs effets.
Dans les configurations (b), les spins étant anti-parallèles, le moment magnétique résultant est nul.
Exemple, l’hélium \(He\) : 2 électrons sur la couche \(K~(n=1)\).
L’absence de propriétés magnétiques envisagée ci-dessus indique que les deux électrons ont leurs spins antiparallèles.
Il semble interdit dans une configuration stable que les deux électrons de la couche \(K\) aient des spins identiques.
4.2. Généralisation
Un électron est caractérisé par quatre nombres quantiques {\(n,~l,~j,~j_z\)}, \(j_z\) étant la projection de \(j\) sur l’axe de quantification.
Le principe de Pauli postule alors qu’il est impossible que deux électrons du cortège possèdent les mêmes valeurs des 4 nombres quantiques.
Le principe limite à un certain nombre de combinaisons à priori .
Pour la couche \(K\), le nombre d’électrons est limité à 2.
Pour la couche \(L~(n=2)\) :
-
sur le niveau \(l=0\) : 2 électrons ;
-
sur le niveau \(l=1\) : 6 électrons, au plus.
5. Atome et photon : interactions
5.1. Absorption
Quand un photon pénètre dans l’atome, son énergie {\(E=h~\nu\)} peut être utilisée pour éloigner un électron du noyau positif qui le retient. Il peut alors passer par exemple de la couche \(L\) à la couche \(M\) en absorbant l’énergie {\(E_L-E_M\)}.
Si l’énergie du photon est suffisante, l’électron (de \(L\) par exemple) peut être propulsé hors de l’atome avec l’énergie cinétique : \[W=h~\nu-E_L\]
C’est le principe de la cellule photoélectrique.
5.2. Émission
Le phénomène inverse est aussi possible. Par exemple, une place étant vacante sur une orbite électronique (couche \(K\) par exemple), un électron \(L\) tombe sur la couche \(K\) en émettant un photon d’énergie {\(h~\nu=E_K-E_L\)}.
Si la transition a lieu entre des couches profondes, la fréquence \(h~\nu\) du photon émis est grande et le rayonnement émis est un rayonnement \(X\).
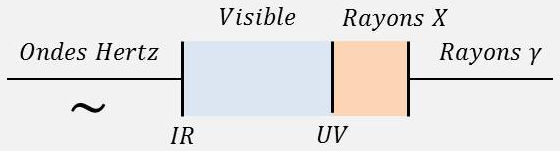 Si la transition a lieu entre des couches externes de l’atome, les énergies de liaison correspondant à ces couches sont faibles, la fréquence émise également, le rayonnement est un rayonnement optique (spectre ultra-violet et visible).
Si la transition a lieu entre des couches externes de l’atome, les énergies de liaison correspondant à ces couches sont faibles, la fréquence émise également, le rayonnement est un rayonnement optique (spectre ultra-violet et visible).

