1. Définition et caractéristiques

Les transformations entrant dans la constitution du groupe de symétrie d’un corps de dimensions finies (donc la molécule) doivent être telles qu’elles conservent au moins un point lorsqu’on applique n’importe laquelle de ces transformations.

Tous les axes et plans de symétrie doivent donc avoir au moins un point commun. En effet, à la suite de deux rotations consécutives autour d’axes non concourants ou à la suite de réflexions dans deux plans ne se coupant pas, le corps ne se superpose pas à lui-même, pour n’avoir subi qu’une translation.

Les groupes de symétrie jouissant de ces propriétés de conservation minimale sont appelés groupes ponctuels.

NB : Pour les distinguer de leurs éléments, les noms de groupe sont écrits en lettres grasses.

2. Groupes ponctuels possibles

2.1. Groupes \(\textbf{C}_n\)

Le groupe \(\textbf{C}_n\) est celui des rotations autour d’un axe de symétrie n-aire. Il est cyclique.

Chacun des \(n\) éléments de ce groupe constitue une classe en soi.

Le groupe particulier \(\textbf{C}_1\) est constitué par la seule transformation identique \(E\).

2.2. Groupe \(\textbf{S}_{2n}\)

Le groupe \(\textbf{S}_{2n}\) est celui des rotations autour d’un axe de réflexion-rotation d’ordre pair \(2~n\).

Il contient \(2~n\) éléments et il est cyclique.

\(\textbf{S}_2\) (nommé également \(\textbf{C}_i\)) ne contient que deux éléments : \(E\) et \(I\).

Noter que si l’ordre du groupe peut être présenté sous la forme \[2~n~=~4~p~+~2\]

alors l’inversion se trouve parmi ses éléments.

Il est évident que : \[(\textbf{S}_{4p+2})^{2p+1}~=~\textbf{C}_2~\sigma_h~=~\textbf{I}\]

Un tel groupe peut s’écrire sous forme de produit direct : \[\textbf{S}_{4p+2}~=~\textbf{C}_{2p+1}~\times~\textbf{C}_i\]

On le note également \(\textbf{C}_{2p+1,~i}\)

2.3. Groupes \(\textbf{C}_{nh}\)

Les groupes \(\textbf{C}_{nh}\) s’obtiennent en associant à un axe de symétrie n-aire un plan de symétrie perpendiculaire.

\(\textbf{C}_{nh}\) contient \(2~n\) éléments :

• \(n\) rotations de \(\textbf{C}_n\) ;

• \(n\) réflexion-rotation \(C_n^k\sigma_h\) (\(k=1,~2,~\dots,~n\)) dont la réflexion \(C_n^n~\sigma_h=\sigma_h\).

Tous les éléments du groupe sont commutatifs (groupe abélien) ; le nombre de classes est égal au nombre des éléments.

Si \(n\) est pair (\(n=2~p\)), alors le groupe contient le centre de symétrie puisque : \[C_{2p}^p~\sigma_h~=~C_2~\sigma_h~=~I\]

Le groupe le plus simple \(\textbf{C}_{1h}\) (noté \(\textbf{C}_s\) contient en tout deux éléments (\(E\) et \(\sigma_h\)).

2.4. Groupes \(\textbf{C}_{nv}\)

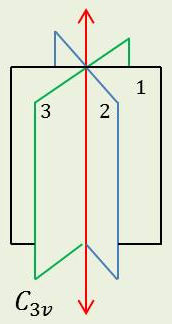Si on associe à un axe de symétrie n-aire un plan de symétrie contenant cet axe, on obtient automatiquement (\(n-1\)) autres plans axiaux se coupant sous \(\pi/n\).

Le groupe \(\textbf{C}_{nv}\) contient par conséquent \(2~n\) éléments :

• \(n\) rotations autour de l’axe n-aire ;

• \(n\) réflexions dans les plans verticaux \(\sigma_v\).

On a représenté \(\textbf{C}_{3v}\) sur la figure ; un livre posé verticalement donne une idée des suivantes.

2.5. Groupes \(\textbf{D}_n\)

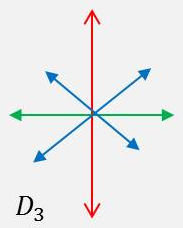Si l’on associe à un axe de symétrie n-aire un axe binaire orthogonal, on obtient alors automatiquement (\(n-1\)) axes de ce genre, de sorte que l’on a en tout \(n\) axes horizontaux binaires se coupant deux à deux sous (\(\pi/n\)).

Le groupe \(\textbf{D}_n\) ainsi obtenu contient \(2~n\) éléments :

• \(n\) rotations autour de l’axe n-aire ;

• \(n\) rotations d’angle \(\pi\) autour des axes horizontaux.

On désigne généralement ces dernières par \(U_2\), la notation \(C_2\) étant réservée à la rotation de \(\pi\) autour de l’axe vertical.

Un cas particulier important \(\textbf{D}_2\) (également noté \(\textbf{V}\)) : trois axes orthogonaux binaires.

2.6. Groupe \(\textbf{D}_{nh}\)

Si l’on ajoute au système d’axes du groupe \(\textbf{D}_n\) un plan de symétrie horizontal contenant les n axes binaires, on obtient alors automatiquement \(n\) plans verticaux définis respectivement par l’axe vertical et les axes horizontaux.

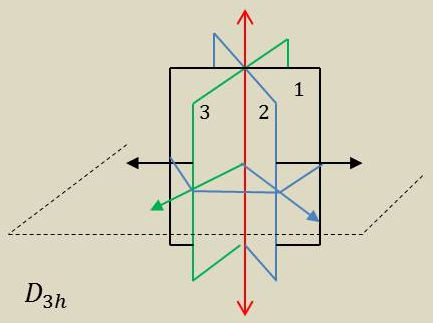Le groupe \(\textbf{D}_{nh}\) obtenu alors contient \(4~n\) éléments :

• \(2~n\) éléments du \(\textbf{D}_n\) de base ;

• \(n\) réflexions \(\sigma_v\) ;

• \(n\) transformations de réflexion-rotation \(C_n^k~\sigma_h\).

Notons que la réflexion \(\sigma_h\) commute avec tous les autres éléments du groupe.

On peut donc écrire \(\textbf{D}_{nh}\) sous forme d’un produit direct : \[\textbf{D}_{nh}~=~\textbf{D}_n~\times~\textbf{C}_s\]

\(\textbf{C}_s\) : groupe des deux éléments \(E\) et \(\sigma_h\).

Lorsque \(n\) est pair, l’inversion fait partie des éléments du groupe, et on peut écrire : \[\textbf{D}_{2p,~h}~=~\textbf{D}_{2p}~\times~\textbf{C}_i\]

2.7. Groupe \(\textbf{D}_{nd}\)

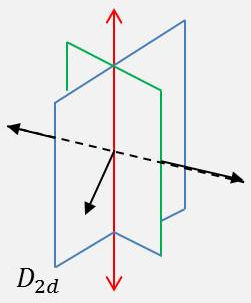Il existe encore un mode d’association de plans de symétrie au système d’axes du groupe \(\textbf{D}_n\). Ce sont précisément les plans verticaux bissecteurs des axes horizontaux binaires.

Ici encore l’association d’un tel plan entraîne l’apparition des (\(n-1\)) autres plans.

Le système d’axes et de plans de symétrie obtenu détermine le groupe \(\textbf{D}_{nd}\).

Le groupe \(\textbf{D}_{nd}\) contient \(4~n\) éléments :

• \(2~n\) éléments de \(\textbf{D}_n\) ;

• \(n\) réflexions dans les plans verticaux notés \(\sigma_d\) (diagonaux) ;

• \(n\) transformations de la forme \(G~=~U_2~\sigma_d\).

Notons que nous pouvons exprimer également la rotation \(U_2\) sous la forme : \[U_2~=~\sigma_h~\sigma_v\]

\(\sigma_v\) : réflexion dans le plan vertical passant par l’axe binaire donné.

On a alors : \[G~=~\sigma_h~\sigma_v~\sigma_d\]

sachant que les transformations \(\sigma_v,~\sigma_d\) ne sont pas elles-mêmes des éléments du groupe.

2.8. Groupe du tétraèdre \(\textbf{T}\)

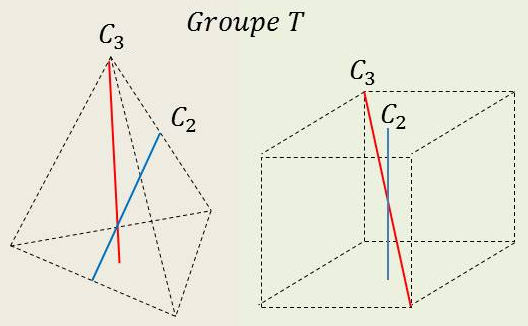Le système d’axes du groupe \(\textbf{T}\) peut être obtenu en associant au système d’axes du groupe V quatre axes obliques 3-aires les rotations autour desquels transforment l’un dans l’autre les trois axes binaires.

Pour se représenter ce système, on identifie :

• les trois axes binaires avec les perpendiculaires des faces du cube en leurs centres ;

• les axes 3-aires avec les diagonales spatiales du cube.

2.9. Groupe \(\textbf{T}_d\)

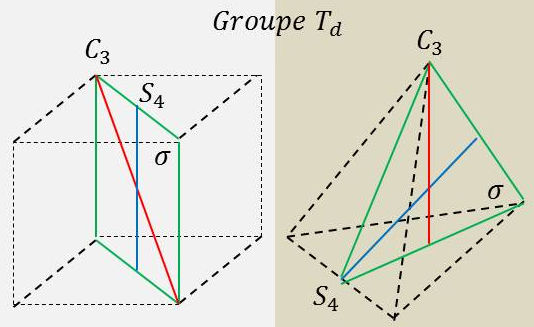Le groupe \(\textbf{T}_d\) contient toutes les transformations de symétrie du tétraèdre.

On peut obtenir son système d’axes et de plans en associant aux axes du groupe T des plans de symétrie, chacun d’eux contenant un axe binaire et deux axes ternaires.

Alors, les axes binaires deviennent des axes de réflexion-rotation 4-aires (comme cela a lieu dans le groupe \(\textbf{D}_{2d}\)).

Il est commode de se représenter ce système en dessinant les trois axes de réflexion-rotation par les centres des faces opposées du cube, les quatre axes ternaires en tant que diagonales spatiales, les six plans de symétrie contenant chacun deux arêtes opposées.

Les plans de symétrie étant verticaux vis-à-vis des axes ternaires, ceux-ci sont bilatères.

2.10. Groupe \(\textbf{T}_h\)

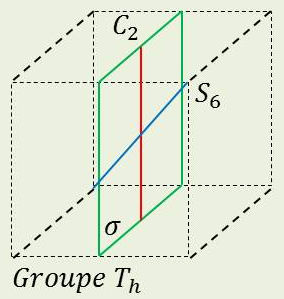Le groupe \(\textbf{T}_h\) est déduit de \(\textbf{T}\) en ajoutant un centre de symétrie : \[\textbf{T}_d~=~\textbf{T}~\times~\textbf{C}_i\]

Ceci entraîne l’apparition de trois plans de symétrie orthogonaux contenant chacun deux axes binaires.

Les axes ternaires deviennent des axes de réflexion-rotation 6-aires.

On a représenté sur la figure un axe et un plan de chaque espèce.

2.11. Groupe de l’octaèdre \(\textbf{O}\)

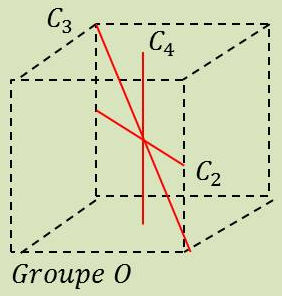Le système d’axes du groupe O est celui des axes de symétrie du cube :

• trois axes 4-aires passent par les centres des faces opposées ;

• quatre axes 3-aires passent par les sommets des faces opposées ;

• six axes 2-aires passent par les milieux des arêtes opposées.

Les axes de même ordre sont équivalents, chacun d’eux étant bilatère.

D’où la répartition des 24 éléments dans les 5 classes suivantes :

\(E\), 8 rotations (\(C_3\) et \(C_3^2\)), 6 rotations (\(C_4\) et \(C_4^2\)), 3 rotations \(C_4^2\), 6 rotations \(C_2\).

2.12. Groupe \(\textbf{O}_h\)

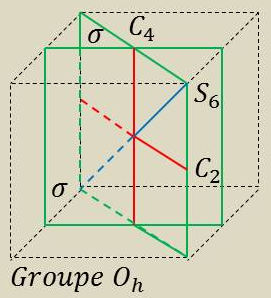Le groupe \(\textbf{O}_h\) est celui de toutes les transformations de symétrie du cube.

Ce groupe s’obtient en ajoutant au groupe O un centre de symétrie : \[\textbf{O}_h~=~\textbf{O}~\times~\textbf{C}_i\]

Les axes ternaires de O deviennent alors des axes de réflexion-rotation 6-aires (diagonales spatiales du cube).

Apparaissent encore en outre six plans de symétrie contenant chacun deux arêtes opposées, et trois plans parallèles aux faces du cube.