1. Transformations élémentaires. Rappel

\[\begin{matrix} &\textbf{Élément de symétrie}& &\textbf{Symbole commun}& &\textbf{Opération de symétrie}\\ &\text{Aucun élément particulier}& &E& &\text{Identité}\\ &\text{Plan de symétrie}& &\sigma& &\text{Réflexion}\\ &\text{Centre de symétrie}& &I& &\text{Inversion}\\ &\text{Axes propres}& &C& &\text{Rotation autour d'un axe}\\ &\text{Axes impropres}& &S& &\text{Rotation autour d'un axe}~+~\\ & & & & &\text{Réflexion~/~plan}~\bot~\text{à cet axe} \end{matrix}\]

La structure électronique d’une molécule est attachée entre autres à sa structure géométrique, la symétrie permettant de trier les états électroniques en fonction de leurs propriétés.

Ainsi, considérant la seule symétrie d’une molécule, il est possible de prédéterminer:

• la présence de moments dipolaires permanents ;

• l’activité optique ;

• la construction et la classification des orbitales moléculaires ;

• les règles de sélection de transition ;

• le degré de dégénérescence des états.

2. Autour de la molécule d’ammoniac \(NH_3\)

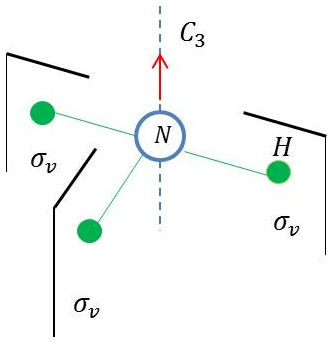Les transformations laissant \(NH_3\) inchangée (isométriques) sont :

• une rotation propre \(C_3\) (\(\theta=2\pi/3\)) ;

• une réflexion \(\sigma_v\) (plan vertical contenant une branche atome \(H\)).

Pour \(NH_3\), les éléments de symétrie sont :

• l’axe \(C_3\) pour la rotation \(C_3\) ;

• les plans verticaux \(\sigma_v,~\sigma_v',~\sigma_v''\) pour la réflexion \(\sigma\).

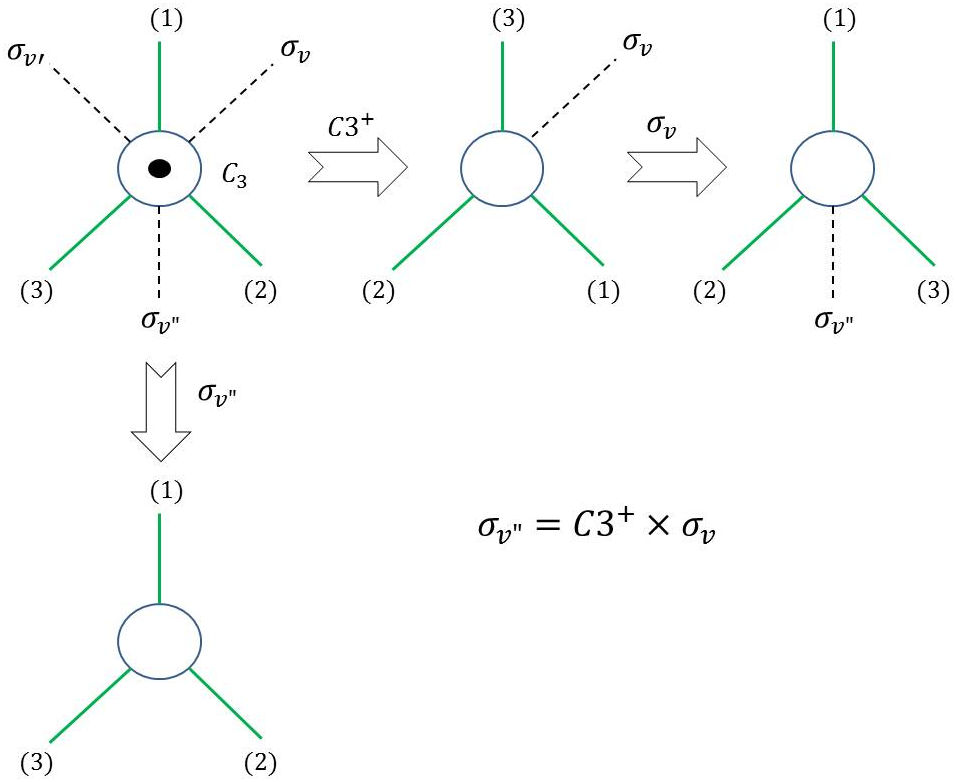Un exercice intéressant est celui des transformations successives (composition de transformations) sur cette même molécule \(NH_3\) (voir figure ci-contre) :

• Première transformation : \(\sigma_v\) suivie de \(C_3^+\) ;

• Deuxième transformation : \(\sigma_{v''}\).

On voit que l’on peut écrire (attention à l’ordre d’écriture des opérations) : \[\sigma_v"~=~\sigma_v~\times~C_3^+\]

La symétrie de la molécule \(NH_3\) relève du groupe \(C_{nv}\), plus exactement du groupe \(C_{3v}\).

Pour \(C_{3v}\), il y a six éléments de symétrie : \(E~;~C_3^+~;~C_3^-~;~\sigma_v~;~\sigma_v'~;~\sigma_v''\).

On écrira : \[C_{3v}~:~~E~;~2~C_3~;~3~\sigma_v\]

On peut construire la table matricielle (ou table de multiplication) du groupe \(C_{3v}\) : \[\begin{matrix} & &E&C_3^+&C_3^-&\sigma_v&\sigma_{v'}&\sigma_{v"}\\ &E&E&C_3^+&C_3^-&\sigma_v&\sigma_{v'}&\sigma_{v"}\\ &C_3^+&C_3^+&C_3^-&E&\sigma_{v'}&\sigma_{v"}&\sigma_v\\ &C_3^-&C_3^-&E&C_3^+&\sigma_{v"}&\sigma_v&\sigma_{v'}\\ &\sigma_v&\sigma_v&\sigma_{v"}&\sigma_{v'}&E&C_3^-&C_3^+\\ &\sigma_{v'}&\sigma_{v'}&\sigma_v&\sigma_{v"}&C_3^+&E&C_3^-\\ &\sigma_{v"}&\sigma_{v"}&\sigma_{v'}&\sigma_v&C_3^-&C_3^+&E \end{matrix}\]

La correspondance se fait entre la première ligne hors tableau \(6\times 6\) et la première colonne hors tableau à gauche.

On pourra ainsi vérifier que : \[\sigma_v"~=~\sigma_v\times C_3^+\]

On pourra remarquer également que : \[\sigma_v\times C_3^+~\neq~C_3^+\times \sigma_v\]

Et notre également que : \[(A~B~C)^{-1}~=~C^{-1}~B^{-1}~A^{-1}\]

Autrement dit, le groupe est non commutatif (abélien).

3. Autour de la molécule d’eau \(H_2O\)

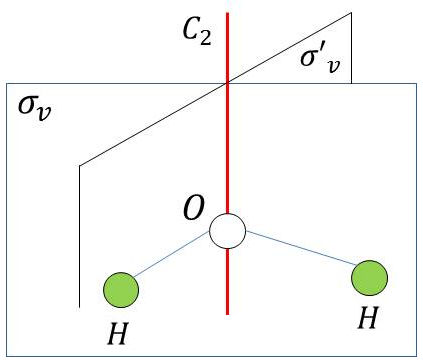Les éléments de symétrie de la molécule d’eau sont :

• \(C_2\) : axe de symétrie ;

• \(\sigma_v\) : plan moléculaire (contient l’axe \(C_2\)) ;

• \(\sigma'_v~\bot~\sigma_v\) : plan moléculaire (contient l’axe \(C_2\)).

Opérations symétriques : \[C_2^1.C_2^2~=~E~~;~~\sigma_v.\sigma_v^2~=~E~~~;~~\sigma'_v.{\sigma'_v}^2~~=~E\]

On écrira : \[C_{2v}~:~E~;~C_2~;~2\sigma_v\]

Tableau du groupe des transformations : \[\begin{matrix} &E&E&C_2^1&\sigma_v&\sigma'_v\\ &E&E&C_2^1&\sigma_v&\sigma'_v\\ &C_2^1&C_2^1&E&\sigma_v&\sigma'_v\\ &\sigma_v&\sigma_v&\sigma'_v&E&C_2^1\\ &\sigma'_v&\sigma'_v&\sigma_v&C_2^1&E \end{matrix}\]

On notera que :

• la loi de composition est interne ;

• il y a un élément neutre ;

• la loi est associative ;

• tout élément a un symétrique par rapport à la diagonale ;

• il s’agit d’un groupe abélien.

4. Aperçu du modèle VSEPR

VSEPR = Valence Shell Electronic Pair Repulsions (répulsion des paires électroniques des couches de valence).

Ce modèle a été proposé par le chimiste canadien R.J Gillepsie

4.1. Un constat à l’origine

On sait que le dioxyde de soufre \(SO_2\) est très soluble, contrairement au dioxyde de carbone \(CO_2\) qui l’est beaucoup moins. Pourtant, leur structure \(AX_2\), en apparence semblable est différente, \(A\) désignant l’atome central (\(S\) ou \(C\)) et \(X\) l’un des deux autres atomes (\(O\)).

Dans la notation \(AX_n\), l’indice \(n\) ne pourra correspondre au nombre total d’électron mais seulement à ceux concernés, les électrons de valence.

Les spectres infrarouge des deux molécules précédentes présentent une différence :

• le spectre pour \(CO_2\) présente une forme linéaire ;

• le spectre pour \(SO_2\) présente une forme coudée.

Ce qui s’interprète de la façon suivante :

• le moment dipolaire de \(SO_2\) n’est pas nul, ce qui explique sa réaction avec l’eau ;

• le moment dipolaire de \(CO_2\) est nul, ce qui signifie qu’il y a compensation des moments dipolaires de liaison.

4.2. Formulation VSEPR de la molécule

On fait le bilan des paires liantes et non liantes et éventuellement l’électron célibataire de la couche externe.

Tous les électrons sont statistiquement équidistants du noyau, comme s’ils se plaçaient à la surface d’une sphère dont le noyau occuperait le centre. Les électrons correspondants se repoussent mutuellement et se localisent dans les positions qui minimisent les répulsions électroniques.

La formulation VSEPR s’exprime par une expression du type : \[A~X_m~E_n\]

• \(m\) : nombre d’atomes \(X\) auxquels est lié l’atome central \(A\)

• \(n\) : nombre d’entités non liantes (doublets libres et électrons célibataires) en propre

C’est donc une somme somme (\(m + n\)) qui définit la géométrie de la molécule.

4.3. Exemples. Structures géométriques

4.3.1. La répartition commune sphérique

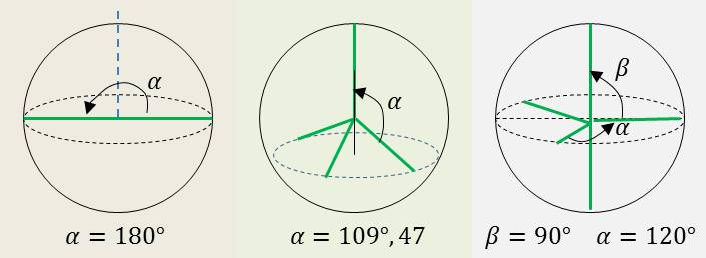On reconnaît sur la figure ci-contre le repérage sphérique qui pourrait être celui de trois molécules bien connues telles que \(CO_2\), \(CH_4\) ou \(PCl_5\).

Les angles \(\alpha\) et \(\beta\) appartenant soit à un plan méridien soit à un plan équatorial, soit à un plan parallèle au précédent.

4.3.2. Principe succinct de nomenclature

Nous raisonnerons simplement sur quelques exemples : \[\begin{matrix} &m+n&\text{polygone}&\text{structure}&\text{forme molécule}&\text{liais. simples}&\text{liais. multiples}\\ &&&&&&&\\ &2&\text{segment}&AX_2E_0&\text{linéaire}&-&CO_2\\ &3&\text{triangle équilat}&AX_2E_1&\text{coudée}&-&SO_2,NO_2\\ &4&\text{tétraèdre}&AX_4E_0&\text{tétraédrique}&CH_4,NH_4^+&SO_4^{2-}\\ &-&-&-&\text{pyram base triangul}&NH_3&-\\ &5&\text{bipyram trigonale}&AX_5E_0&\text{bipyram trigonale}&PCl_5&-& \end{matrix}\]

4.3.3. Comparaison géométrique

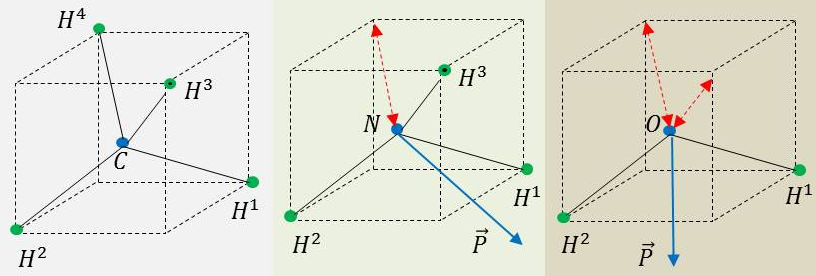Ci-contre les structures du méthane, de l’ammoniac et de l’eau (\(m+n=4\)) pour lesquelles on a respectivement :

\[\begin{aligned} CH_4~&:~4~AX_4E_0 &&\alpha=109,47~^o\\ NH_3~&:~~~AX_3E_1 &&\alpha=107~^o\\ H_2O~&:~~~AX_2E_2 &&\alpha=104,5~^o\end{aligned}\]

Elles ont donc une structure tétraédrique mais l’augmentation des répulsions dues aux paires libres entraînent une réduction de l’angle \(H-A-H\).

5. Classement par transformations

Pour plus de clarté, nous prendrons quelques exemples :

\[\begin{aligned} &\text{molécule} &&\text{symétrie} &&\text{transformations composantes}\\ &H_2O &&C_{3v} &&E,~C_2,~\sigma_v,~\sigma_v'\\ &NH_3 &&C_{3v} &&E,~2~C_3,~3~\sigma_v\\ &PCl_5 &&D_{3h} &&E,~2~C_3,~3~C_2~,~\sigma_h,~2~S_3,~3~\sigma_v\\ &CH_4 &&T_d &&E,~8~C_3,~3~C_2,~6~S_4,~6~\sigma_d\end{aligned}\]