1. Hypothèse adiabatique

1.1. Potentiels et énergies cinétiques

Forme composite du hamiltonien d’une molécule diatomique (\(A-B\)) :

\[\begin{aligned} H~&=~(T_A~+~T_B)~+~(T_e)~+~(V_{AB}~+~V_{e,AB}~+~V_{e,e})\qquad(1) \\ H~&=~ \left\{ \begin{aligned} &~~~~T_A+T_B\qquad\qquad\qquad~~\text{énergies cinétiques nucléaires}\\ &+T_e\qquad\qquad\qquad\qquad~~~~\text{énergies cinétiques électroniques}\\ &+V_{AB}+V_{e,AB}+V_{e,e}\qquad\text{énergies potentielles} \end{aligned} \right.\end{aligned}\]

Expressions des énergies cinétiques et des potentiels :

\[\begin{aligned} T_j&=-\frac{\hbar^2}{2~M_j}~{(j)}~~~~\text{(noyaux)}\quad &&~~T_i=-\frac{\hbar^2}{2~m_i}~\sum_i\Delta_{(i)}~~~\text{(électrons)} &&(2)\\ V_{A,B}&=\frac{(Z_A~Z_B)~e^2}{|\overrightarrow{R}_B-\overrightarrow{R}_A|}~~\text{(noyaux)} &&V_{e,e}=\frac{1}{2}~\sum_{i\neq j}\frac{e^2}{|\overrightarrow{r_i}-\overrightarrow{r_j}|}~~~\text{(électrons)} &&(3)\end{aligned}\]

Expression du potentiel interaction électronique nucléaire : \[V_{e,A,B}~=~-Z_A~\sum_i^N\frac{e^2}{|\overrightarrow{R}_A-\overrightarrow{r}_i|}~-~Z_B~\sum_i^N\frac{e^2}{|\overrightarrow{R}_B-\overrightarrow{r}_i|}\qquad(4)\]

• \(R_A,~R_B,~r_i\) : rayons vecteurs relatifs aux noyaux et aux électrons

• \(\Delta_{j}\) : Laplacien associé à la particule \((j)\)

• \(Z_A,~Z_B\) : nombres de charge respectifs de \(A,B\)

La distance entre particules est exprimée comme le module d’une différence vectorielle.

1.2. Hypothèse de Born et Oppenheimer

Selon l’hypothèse de Born et Oppenheimer, on peut étudier le mouvement des électrons en le découplant, dans un premier temps, de celui des noyaux (dont le mouvement est beaucoup plus lent) : On considère alors les noyaux comme fixes. Les distances entre noyaux devenant alors des paramètres.

On obtient ainsi une présentation allégée des calculs : telle est l’approximation adiabatique. Le système est présenté avec des coordonnées distinguées (\(q_i~;~Q_j\)) :

• \(q_i\) attribuées aux mouvements des électrons (indicés \(i\))

• \(Q_j\) attribuées aux mouvements des noyaux (indicés \(j\))

2. Principe de l’approximation de Born et Oppenheimer

Faisant l’hypothèse de l’attraction coulombienne (potentiel \(V\)), on posera \[\begin{aligned} H~&=~\sum_j T_{N,j}~+~\Big\{\sum_i T_{e,i}~+~V(\{q_i\},\{Q_j\}\Big\}\\ H~&=~[~T_N~]~+~\big\{H_0(p_i,~q_i~;~Q_j)\big\} \end{aligned}\qquad(2)\]

\(p_i\) : impulsion, attachée à l’électron (supposé seul mobile)

2.1. Noyaux fixes, électrons en mouvement

Selon l’hypothèse de Born et Oppenheimer (restriction à l’électronique), on fait \(H\equiv H_0\).

On ne recherchera que les états propres de l’opérateur \(H_0\), les (\(p_i,~q_i\)) étant considérés comme des opérateurs et les {\(Q_j\)} comme des paramètres.

Les énergies propres étant quantifiées et les fonctions propres des états liés normalisées, l’équation aux valeurs propres de \(H_0\) dans la représentation {\(q\)} s’écrit : \[H_0~\Phi_n(q_i~;~Q_j)~=~E_n(Q_j)~~\Phi_n(q_i~;~Q_j)\qquad(3)\]

Les fonctions propres {\(\Phi_n\)} constituent une base complète.

2.2. Noyaux en mouvement

Introduisons un ensemble de \(X_m(Q_j)\) ne dépendant que des coordonnées nucléaires.

La fonction d’onde totale a alors pour expression : \[\Psi(q_i~;~Q_j)~=~ X_m(Q_j)~~\Phi(q_i~;~Q_j)\qquad(4)\]

Puis, revenant à [2] : \[H~\Psi~=~(T_N+H_0)~\Psi~=~E~\Psi\qquad(5)\]

2.3. Approximation adiabatique

En notations de Dirac, on démontre que (approximation adiabatique) : \[\langle~\big\{T_N+E_m(Q_j)\big\}~|~X_m~\rangle~\approx~\langle~E~|~X_m(Q_j)~\rangle\qquad(6)\]

Le nombre quantique \(m\) étant fixé (mouvement des électrons à \(m\) donné), soit \(X_m(Q_j)\) est nulle, soit \(X_m(Q_j)\) est l’une des fonctions propres de l’équation (6).

La fonction d’onde totale devient un simple produit : \[\Psi(q_i~;~Q_j)~\approx~X_m(Q_j)~~\Phi_m(q_i~;~Q_j)~\qquad(7)\]

La lenteur du mouvement nucléaire induit une fréquence de vibration \(\omega_{vib}\) (et à fortiori une fréquence de rotation \(\omega_{rot}\)) toujours très petites devant celle des électrons \(\omega_{el}\).

En résumé :

\[\begin{aligned} \Psi(q_i~;~Q_j)~&=~X_m(Q_j)~~\Phi_m(q_i~;~Q_j) &&(8)\\ H_0~\Phi_m~&=~E_m(Q_j)~~\Phi_m &&(9)\\ \big\{T_N~+~E_m(Q_j)\big\}~~X_m(Q_j)~&=~E~~X_m(Q_j) &&(10)\end{aligned}\]

• \(\Phi_m\) : fonction d’onde (noyaux fixes)

• \(E_m\) : valeur propre correspondante (ne dépend que des \(Q_j\))

• \(X_m\) : mouvement des noyaux

2.4. Caractéristiques de la variation d’énergie

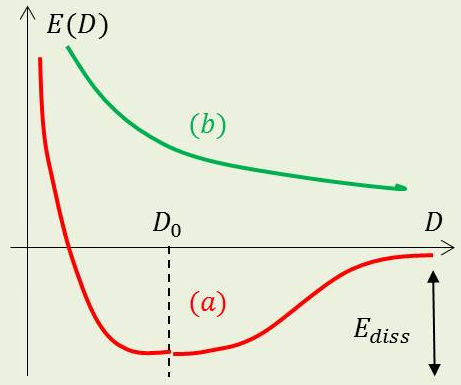L’énergie de la molécule diatomique \(A-B\) n’est fonction que de la distance \(D=AB\) (isotropie de l’espace). Elle a une limite quand \(D\) devient très grand. Elle devient infinie quand \(D\) tend vers 0.

Chaque noyau (ou chaque cœur) s’oppose à l’influence de l’autre sur son domaine personnel.

1) Dans le cas stable (a), un minimum \(D_0\) apparaît. Il lui correspond un état liant \(\Phi_m\).

\(D_0\) est la longueur de la liaison chimique \(A-B\).

L’état ainsi défini est stable et il faut une énergie \(E_{diss}\) pour dissocier la molécule en deux constituants séparés : c’est l’énergie de la liaison chimique.

2) Dans le cas instable (b), il n’y a pas de minimum : l’état \(\Phi_m\) est antiliant.

La molécule se dissocie spontanément (intermédiaire obligé de la photo-dissociation).

3. Rotation et vibration nucléaire. Analyse

La molécule diatomique est un système similaire à celui de deux boules réunies par un ressort.

La force de rappel caractérise la liaison chimique entre les atomes, force due essentiellement au cortège électronique et à son état quantique.

3.1. Vibration nucléaire

3.1.1. Approximation harmonique

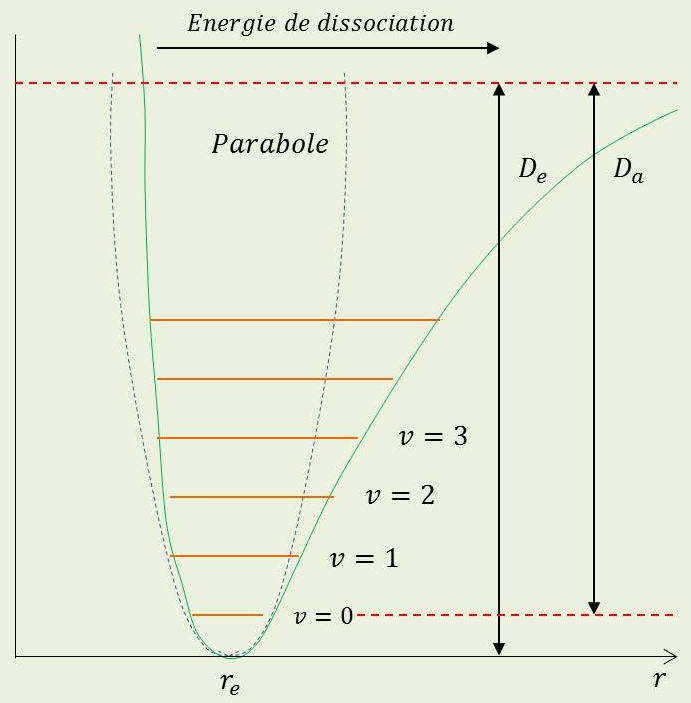En première approximation, l’énergie potentielle d’interaction entre les atomes s’écrit : \[V(r)~=~\frac{1}{2}~k~(r-r_e)^2\qquad(11)\]

\(r_e\) : distance d’équilibre entre les atomes (typiquement \(\approx\) 1 à 2 Å = 0,1 à 0,2 nm).

Les atomes effectuent leurs oscillations (niveaux d’énergie équidistants):

\[\begin{aligned} E_v&=(v+\frac{1}{2})~h~\nu_{vib}\quad;\quad\nu_{vib}~=~\frac{1}{2\pi}\sqrt{\frac{k}{\mu}}\\ \mu&=\frac{m_A~m_B}{m_A+m_B}\qquad(\text{masse réduite})\qquad(12)\end{aligned}\]

3.1.2. Potentiel réel, anharmonique

L’expression précédente de \(V(r)\) suppose de petites déformations (assimilation du creux de la courbe d’énergie à une parabole osculatrice).

En écartant les atomes l’un de l’autre, il y a cassure de la liaison : la force de rappel s’annule et l’énergie potentielle tend vers une constante. En les rapprochant, les nuages électroniques s’interpénètrent et la force de répulsion augmente énormément.

L’écart \(D_e\) entre la limite quand \(r\) devient grand et le fond du puits de potentiel est l’énergie de la liaison chimique (typiquement \(D_e~\approx~5~\)eV).

Caractérisation du potentiel anharmonique :

1) Les niveaux d’énergie ne sont plus équidistants : l’écart entre niveaux successifs diminue avec l’énergie de vibration. La période d’oscillation augmente lorsque l’énergie de vibration se rapproche de l’énergie de dissociation, la force de rappel diminuant fortement lorsque la molécule est très étirée.

2) Le nombre de niveaux de vibration est fini (de l’ordre de quelques dizaines). La représentation mathématique de Morse \(V(r)\) rend bien compte de ces propriétés : \[V(r)~=~D_e~\{1-\exp[-a~(r-r_e)]^2\}\qquad(13)\]

L’équation de Schrödinger pour le mouvement de vibration des noyaux se résout alors analytiquement et donne lieu à une série de niveaux d’énergie dont l’expression est exactement : \[E_v=\Big\{\Big(v+\frac{1}{2}\Big)-x_e~\Big(v+\frac{1}{2}\Big)^2\Big\}~h~\nu_{vib}\qquad(14)\]

• \(x_e\) est le facteur d’anharmonicité.

• \(v\) est un niveau d’énergie donnée.

Les coefficients spectraux sont reliés à l’énergie de dissociation par : \[D_e~=~\frac{(h~\nu_e)^2}{4~h~\nu_e~x_e}\qquad(15)\]

Le nombre de niveaux de vibration est naturellement fini : \[N~\sim~\frac{h~\nu_e}{2~h~\nu_e~x_e}\qquad(16)\]

3.2. Rotation nucléaire

On fait deux hypothèses :

1) La molécule est diatomique, en rotation autour d’un axe perpendiculaire à l’axe internucléaire.

2) La molécule est rigide, donc une interaction ne peut être que négligeable entre un éventuel mouvement de rotation et de vibration de la molécule.

On montre que l’écart d’énergie entre deux niveaux successifs croît proportionnellement à \(J\) :

\[\begin{aligned} E_{rot}(J)-E_{rot}(J-1)~&=~2~B~J~=~\frac{\hbar^2}{2~I}~2~J\\ \text{lim}_{J~\rightarrow~\infty}\big\{E_{rot}(J)-E_{rot}(J-1)\big\}~&=~\frac{h}{2\pi}~\omega_{rot}~=~h~\nu_{rot}\end{aligned}\]

On retrouve le principe de correspondance de Bohr. Ainsi la fréquence caractéristique de rotation dépend de l’énergie de rotation.

Pour des molécules plus lourdes ou plus longues, les fréquences de rotation diminuent et les longueurs d’onde associées augmentent.