1. Loi de décroissance radioactive

Les noyaux des atomes radioactifs possèdent donc la propriété de modifier spontanément leur structure interne de façon à atteindre un niveau d’énergie plus fondamental.

Le noyau résiduel peut être stable, mais il peut être encore radioactif, donc subir à son tour d’autres transformation. Le retour à la stabilité obtenu par cette transformation nucléaire (ou par une série de transformations nucléaires) est le processus de désintégration.

Ce phénomène aléatoire en appelle au traditionnel calcul des probabilités. Il s’apparente à celui des files d’attente, comme le cas des appels téléphoniques pour lesquels la loi de probabilité est la loi de Poisson (voir le calcul des probabilités).

La probabilité de désintégration (proportion des noyaux qui se désintègrent par unité de temps) est la constante radioactive désignée traditionnellement par \(\lambda\).

La variation (diminution) \(\Delta N\) du nombre \(N\) de noyaux pendant un temps très court \(\Delta t\) peut donc être exprimée par : \[\Delta N=-\lambda~\Delta t~N\]

Ce qui pourrait s’écrire, à la limite (\(\Delta t~\rightarrow~0\)) : \[dN=-\lambda~dt~N\]

Équation différentielle élémentaire dont la solution (loi de décroissance de Poisson) est : \[N(t)=N_0~\exp(-\lambda~t)\]

• \(N_0\) : nombre de noyau présents à la date \(t=0\)

• \(N(t)\) : nombre de noyaux présents à l’instant \(t\)

• \(\lambda\) : constante de temps radioactive

Le terme \(\lambda~t\) étant sans dimension, la constante \(\lambda\) s’exprime comme l’inverse d’un temps, c’est-à-dire en \(\rm s^{-1}\).

Remarques

1. Dans ce qui précède, nous avions supposé \(t=0\) pour l’instant initial.

   D’une manière plus générale (temps initial \(t_0\)) : \[N(t)=N_0~\exp\lambda~(t-t_0)\quad;\quad N_0=N(t_0)\]

2. Lorsqu’un nucléide peut se transformer en plusieurs modes, la constante \(\lambda\) est la somme des divers modes (conséquence de la somme des probabilités) : \[\lambda=\lambda_1+\lambda_2+\dots\]

2. Constante radioactive. Période de demi-vie

2.1. Constante radioactive et constante de temps

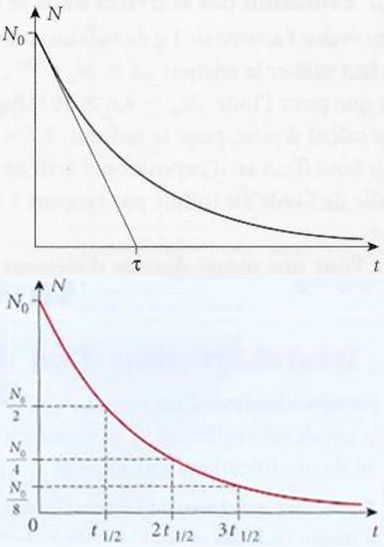Considérons le graphe de représentation de \(N(t)\). La pente de la tangente à l’origine est donnée par : \[\Big[\frac{dN}{dt}\Big]_{t=0}=\Big[-\lambda~N_0~\exp(\lambda~t)\Big]_{t=0}=-\lambda~N_0\]

D’où l’équation de la tangente : \[y(t)=-\lambda~N_0~t+N_0\]

Faisant ensuite \(y(\tau)=0\), un rapide calcul donne ce résultat remarquable : \[\tau=\frac{1}{\lambda}\]

La constante radioactive et la constante de temps sont inverses l’une de l’autre.

La constante radioactive varie pour tous les isotopes connus dans un domaine relativement large : \[1,57\times 10^{-18}~\rm s^{-1}~\leq~\lambda~\leq~3\times 10^6~s^{-1}\]

2.2. Période de demi-vie

La durée \(T_0\) (que l’on voit souvent écrite \(T_{1/2}\)) au bout de laquelle la population de noyaux est divisée par deux est appelée temps de demi-vie ou encore période radioactive.

Pour cela, on écrit : \[\frac{N(t=T_0)}{N_0}=\exp (-\lambda~T_0)=\frac{1}{2}\]

On a donc \[T_0~(\text{ou}~T_{1/2})=\frac{\ln(2)}{\lambda}=\frac{0,693}{\lambda}\]

Relation très importante entre la période de demi-vie et la constante radioactive.

2.3. Remarque

Il peut arriver que le radio-isotope se désintègre suivant deux voies distinctes caractérisées par les périodes respectivement notées \(T_0^{(1)}\) et \(T_0^{(2)}\).

La demi-vie de ce nucléide est définie par la moyenne : \[T_0=\frac{1}{\cfrac{1}{T_0^{(1)}}+\cfrac{1}{T_0^{(2)}}}\]

On en déduit le nombre de nucléides par la relation : \[N(t)=N_0~\exp\{-(\lambda_1+\lambda_2)~t\}\]