1. Définition

On appelle filiation le processus de stabilisation d’un noyau, appelé père (ou bien mère), en une succession de désintégrations. On peut parler aussi de série de décroissance radioactive. À chaque étape (ou état intermédiaire) est engendré un noyau nouveau appelé appelé nucléide fils (ou bien fille).

On écrira symboliquement pour un état stabilisé : \[X_1^*~~\rightarrow~~X_2^*~~\rightarrow~~\cdots~\rightarrow~~X_n\]

La présence du symbole \(^*\) indique que l’élément en question est encore radioactif.

On notera dans cette formule que l’élément \(n\) obtenu est stable (donc au bout de \(n\) itérations), alors que les éléments intermédiaires sont encore radioactifs.

2. Étude d’une transition simple

On considère le cas du noyau \(X_1\) qui se transforme en le noyau \(X_2\), noyau consécutif qui tend vers la stabilité.

On fait naturellement l’hypothèse que le matériau \(X_2\) n’existe initialement qu’en quantité négligeable (ceci pour pouvoir initier l’écriture du processus). On part donc des conditions initiales (\(t=0\)) : \[N_1(t=0)~=~N_0\quad;\quad N_2(t=0)~=~0\]

Rappelons la loi de décroissance radioactive : \[dN~=~-\lambda~N~dt\quad\Rightarrow\quad N(t)~=~N_0~\exp(-\lambda~t)\]

On aura respectivement et consécutivement :

\[\begin{aligned} dN_1~&=~-\lambda_1~N_1~dt &&\Rightarrow\quad N_1(t)~=~N_0~\exp(-\lambda~t)\\ dN_2~&=~(+\lambda_1~N_1~dt)-\lambda_2~N_2~dt\end{aligned}\]

En combinant les deux relations, on obtient : \[\frac{dN_2}{dt}+\lambda_2~N_2~=~\lambda_1~N_1~=~\lambda_1~N_0~\exp(-\lambda~t)\]

La résolution de cette équation différentielle du premier ordre se fait de manière classique en deux étapes :

• résolution de l’équation sans second membre :

• recherche d’une solution particulière de l’équation avec second membre.

Tous calculs faits, on obtient la solution : \[N_2(t)~=~\frac{\lambda_1~N_0}{\lambda_2-\lambda_1}~\{\exp(-\lambda_1~t)-\exp(-\lambda_2~t)\}\]

Cette relation montre que : \[N_2(t=0)=0\quad\text{et}\quad N_2(t=\infty)=0\]

Il existe donc un maximum. On montre qu’il correspond à un temps tels que : \[T_m~=~\frac{1}{\lambda_1-\lambda_2}~\ln\frac{\lambda_1}{\lambda_2}\]

La connaissance de \(T_m\) permet de suivre l’évolution d’un produit radioactif, d’où son intérêt en médecine nucléaire.

3. Équilibre radioactif

Dans l’étude de la transition père – fils (ou mère – fille), nous nous intéresserons aux trois cas suivants : \[\lambda_1\ll\lambda_2\quad;\quad\lambda_1<\lambda_2\quad;\quad\lambda_2<\lambda_1\]

Ils correspondent respectivement à ce que l’on appelle un équilibre séculaire, un équilibre transitoire et un non-équilibre.

3.1. Équilibre séculaire (\(\lambda_1\ll\lambda_2\))

L’équilibre est dit séculaire quand le temps de demi-vie du père est nettement plus grande que celle du fils, c’est-à-dire que l’activité du père est nettement plus faible que celle du fils.

Reprenons la relation précédente : \[N_2(t)~=~\frac{\lambda_1~N_0}{\lambda_2-\lambda_1}~\{\exp(-\lambda_1~t)-\exp(-\lambda_2~t)\}\]

et considérons à présent l’activité : \[A_2(t)~=~\lambda_2(t)~N_2(t)\]

On peut écrire ainsi : \[A_2(t)~=~\frac{\lambda_2~A_0}{\lambda_2-\lambda_1}~\{\exp(-\lambda_1~t)-\exp(-\lambda_2~t)\}\]

Dans l’hypothèse où \(\lambda_1\ll\lambda_2\) : \[A_2(t)~=~A_0~\{\exp(-\lambda_1~t)-\exp(-\lambda_2~t)\}\]

Si nous supposons de plus que \(\lambda_1\approx 0\) : \[A_2(t)~=~A_0~\{1-\exp(-\lambda_2~t)\}\]

Remarquons enfin que pour \(t\rightarrow\infty\) : \[A_2(t)~\approx~A_0~\exp(-\lambda_1~t)~=~A_1(t)\]

On peut donc dire que les activités parent – descendant deviennent équivalentes après un temps suffisamment grand.

3.2. Équilibre transitoire (\(\lambda_1<\lambda_2\))

Nous avons écrit de manière générale que : \[A_2(t)~=~\frac{\lambda_2~A_0}{\lambda_2-\lambda_1}~\{\exp(-\lambda_1~t)-\exp(-\lambda_2~t)\}\]

C’est-à-dire : \[A_2(t)~=~\frac{\lambda_2}{\lambda_2-\lambda_1}~A_1(t)\]

On remarque que : \[\frac{\lambda_2}{\lambda_2-\lambda_1}~>~1\]

Ce qui montre que, après un temps suffisamment long, non seulement l’activité de l’isotope descendant est parallèle à celle de l’isotope ascendant mais que, de plus, elle lui est supérieure.

3.3. Non-équilibre (\(\lambda_1>\lambda_2\))

Reprenons la formule de base : \[A_2(t)~=~\frac{\lambda_2~A_0}{\lambda_2-\lambda_1}~\{\exp(-\lambda_1~t)-\exp(-\lambda_2~t)\}\]

Après un temps suffisamment long, seule l’activité de l’élément fils restera : \[A_2(t)~=~\frac{\lambda_1~A_0}{\lambda_1-\lambda_2}~\exp(-\lambda_2~t)\}\]

Après un temps \(T_{max}\), l’activité de l’élément fils atteindra une valeur maximale pour : \[\frac{dA_2(t)}{dt} ~=~\frac{\lambda_2~A_0}{\lambda_2-\lambda_1}~\{\lambda_2~\exp(-\lambda_2~t)-\exp(-\lambda_1~t)\}~=~0\]

On en déduit que : \[\lambda_2~\exp(-\lambda_2~t)~=~\exp(-\lambda_1~t)\]

Et l’occasion de retrouver une relation précédemment établie : \[T_m~=~\frac{1}{\lambda_2-\lambda_1}~\ln\frac{\lambda_2}{\lambda_1}\]

4. Exemples de périodes radioactives. Une famille : \(\rm ^{238}U\)

Pour conclure sur l’ensemble de ces phénomènes radioactifs :

• ordres de grandeur des périodes radioactives de quelques éléments (naturels et artificiels) ;

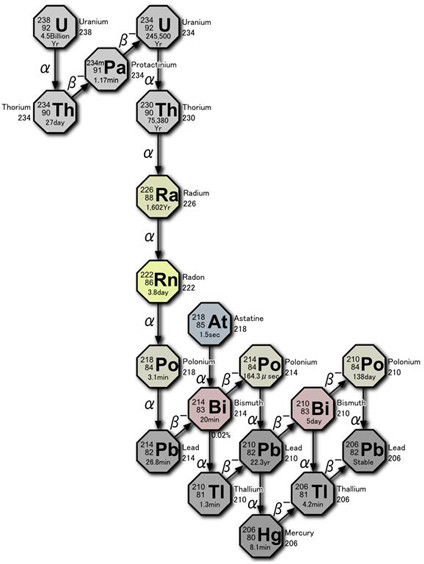
• exemple de la famille radioactive de l’uranium 238 (source Wikipédia).

\[\begin{vmatrix} &\text{Nucléide}&\text{Décroiss.}&\text{Période}\\ &---&---&---\\ &\rm ^{232}Th&\alpha&10^{10}~\rm ans\\ &\rm ^{238}U&\alpha&10^9~\rm ans\\ &\rm ^{235}U&\alpha&10^8~\rm ans\\ &\rm ^{233}U&\alpha&10^5~\rm ans\\ &\rm ^{239}Pu&\alpha&10^4~\rm ans\\ &\rm ^{238}Pu&\alpha&88~\rm ans\\ &\rm ^{226}Ra&\alpha&10^3~\rm ans\\ &\rm ^{242}Cm&\alpha&160~\rm j\\ &---&---&---\\ &\rm ^{40}K&\beta^-&10^9~\rm ans\\ &\rm ^{14}C&\beta^-&10^3~\rm ans\\ &\rm ^{3}H&\beta^-&12~\rm ans\\ &\rm ^{60}C&\beta^-&5,3~\rm ans\\ &\rm ^{131}I&\beta^-&8~\rm j\\ &\rm ^{16}N&\beta^-&7,1~\rm sec\\ &---&---&---\\ &\rm ^{58}Co&\beta^+&20~\rm min\\ &\rm ^{18}F&\beta^+&110~\rm min \end{vmatrix}\]