1. Lumière polarisée

Nous avons défini l’incidence brewstérienne \(i_B\) pour laquelle \(r_{\parallel}=0\). Cela voulait dire qu’après réflexion, la composante parallèle d’une lumière naturelle disparaissait et que n’était réfléchie que sa composante circulaire.

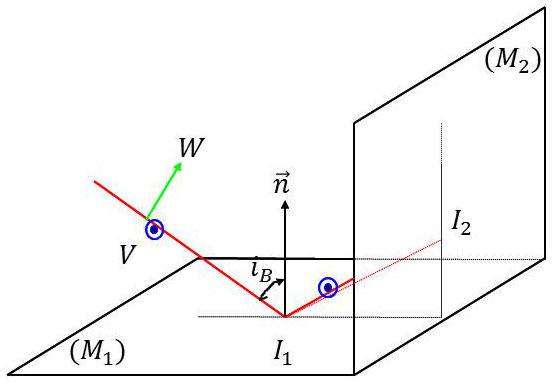La réflexion brewstérienne permet d’obtenir une lumière polarisée perpendiculairement au plan d’incidence.

Un rayon composé des vibrations (\(\overrightarrow{V},~\overrightarrow{W}\)) tombe en incidence brewstérienne sur le miroir \(M_1\) : la vibration \(W\) est alors éliminée.

Après réflexion, le rayon tombe sur un miroir \(M_2\) et il est réglé lui aussi en incidence brewstérienne : la vibration \(V\) est alors éliminée et plus aucune lumière ne sort de l’ensemble.

Un tel dispositif est ce que l’on appelle un polariseur.

L’intensité est maximale lorsque les plans d’incidence coïncident. Elle est nulle lorsqu’ils sont perpendiculaires.

1.1. Remarques

1) Calculons les coefficients de réflexion pour l’onde qui se réfléchit dans le cas de l’incidence brewstérienne. On sait que \(r_{\parallel}=0\), donc \(R_{\parallel}=0\) : \[r_{\bot}=\frac{\sin(i_2-i_1)}{\sin(i_2+i_1)}= \frac{\sin i_2~\cos i_1-\sin i_1~\cos i_2}{\sin i_2~\cos i_1+\sin i_1~\cos i_2}\]

En divisant les deux termes de la fraction par \(\cos i_2~\cos i_1\) : \[r_{\bot}=\frac{\tan i_2-\tan i_1}{\tan i_2+\tan i_1}\]

D’autre part : \[i_1+i_2=\frac{\pi}{2}\quad\Rightarrow\quad\tan i_2=\frac{1}{\tan i_1}\quad\Rightarrow\quad\tan i_1=\frac{n_2}{n_1}=n\]

On a donc : \[r_{\bot}=\frac{(1/n)-n}{(1/n)+n}=\frac{1-n^2}{1+n^2}\]

L’énergie réfléchie sera donnée par : \[R=R_{\bot}=(r_{\bot})^2=\Big(\frac{1-n^2}{1+n^2}\Big)^2\]

2) La lumière naturelle peut être considérée comme formée de deux vibrations perpendiculaires d’amplitudes égales et cohérentes. On peut les choisir (comme cela a été fait plus haut) perpendiculaires et parallèles au plan d’incidence. Du point de vue réflexion de l’intensité, on doit écrire : \(R=R_{\parallel}+R_{\bot}\).

Or, \(R_{\bot}>R_{\parallel}\), sauf pour \(i_1=0\) et \(i_1=\cfrac{\pi}{2}\). C’est pourquoi on est amené à dire que la lumière réfléchie est partiellement polarisée tandis que la polarisation est totale (\(r_{\parallel}=R_{\parallel}\)=0) à l’incidence brewstérienne.

1.2. Loi de Malus

Soit \(E_m\) l’amplitude de la vibration réfléchie par \(M_1\), c’est à dire la vibration perpendiculaire au plan d’incidence sur \(M_1\).

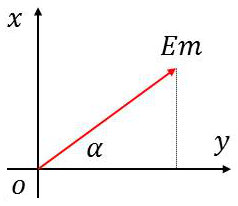Supposons que \(M_2\) soit quelconque (\(Ox\) étant la direction perpendiculaire au plan d’incidence de \(M_2\) et \(Oy\) la direction perpendiculaire). Si on décompose \(E_m\) sur \(Ox\) et \(Oy\), seule sera réfléchie par \(M_2\) la composante portée par \(Ox\) : \[E_x=E_m~\cos\alpha\]

L’intensité réfléchie par les deux miroirs est donc : \[I=E_m^2~\cos^2\alpha\]

C’est la loi de Malus.

2. Étude d’une réflexion dans le cas général

Lorsque la vibration fait un angle \(\theta\) quelconque avec la normale au plan d’incidence, on décompose \(\overrightarrow{E_1}\) en deux vibrations perpendiculaires cohérentes : \[E_1~\cos\theta\qquad;\qquad E_1~\sin\theta\]

Elles deviennent, après réflexion : \[E_1~r_{\bot}~\cos\theta\qquad;\qquad E_1~r_{\parallel}~\sin\theta\]

On a donc : \[{E'_1}^2=E_1^2~r_{\bot}^2~\cos^2\theta+E_1^2~r_{\parallel}^2~\sin^2\theta= E_1^2~(R_{\bot}~\cos^2\theta+R_{\parallel}~\sin^2\theta)\]

D’où on déduit : \[R=\frac{{E'_1}^2}{E_1^2}\]

2.1. Remarque

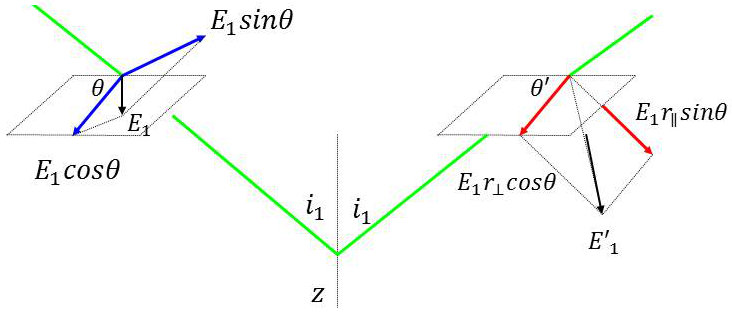Après réflexion, le sens de la composante parallèle de \(\overrightarrow{E}\) a été changé. Par contre, la composante perpendiculaire a été conservée. Dans l’étude d’une transmission, les deux composantes sont généralement respectées.

Après réflexion, la vibration sera rectiligne mais fait avec la normale au plan d’incidence un angle \(\theta'\) tel que :

\[\begin{aligned} &\tan\theta'=\frac{E_1~r_{\parallel}~\sin\theta}{E_1~r_{\bot}~\cos\theta}=\tan\theta~\frac{r_{\parallel}}{r_{\bot}}\\ &\tan\theta'=\tan\theta~\frac{\cos(i_2+i_1)}{\cos(i_2-i_1)}\end{aligned}\]

Après réflexion, la vibration incidente tourne de \((\theta-\theta')\).

En ce qui concerne le déphasage, à condition que \(r\in\mathbb{C}\) , on a : \[\varphi=\varphi_{\parallel}-\varphi_{\bot}=\arg\Big(\frac{r_{\parallel}}{r_{\bot}}\Big)\]

On a donc :

\[\begin{aligned} &\frac{r_{\parallel}}{r_{\bot}}=\frac{\cos(i_2+i_1)}{\cos(i_2-i_1)}= \frac{\cos i_2 \cos i_1-\sin i_2 \sin i_1}{\cos i_2 \cos i_1+\sin i_2 \sin i_1}\\ &\frac{r_{\parallel}}{r_{\bot}}=-\frac{\sin i_2 \sin i_1+j m \cos _1}{\sin i_2 \sin i_1-j m \cos _1}= e^{j~(\varphi+\pi)}\end{aligned}\]

On voit que l’on a : \[\tan\Big(\frac{\varphi}{2}+\frac{\pi}{2}\Big)=\frac{m~\cos i_1}{\sin i_1~\sin i_2}= \frac{\cos i_1~\sqrt{\sin^2i_1-n^2}}{\sin^2i_1}\]

Considérons les valeurs particulières :

\[\begin{aligned} i_1=l~~\Rightarrow~~\sin i_1=n\qquad&\text{donc :}\quad\tan\Big(\frac{\varphi}{2}+\frac{\pi}{2}\Big)=0~~;~~\varphi=0\\ i_1=\frac{\pi}{2}~~\Rightarrow~~\cos i_1=0\qquad&\text{donc :}\quad\tan\Big(\frac{\varphi}{2}+\frac{\pi}{2}\Big)=0~~;~~\varphi=0\end{aligned}\]

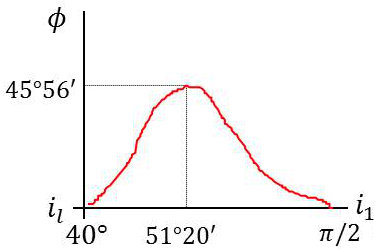L’étude de la dérivée par rapport à \(i_1\) montre que \(\varphi\) est maximale lorsque : \[\tan\frac{\varphi_m}{2}=\frac{1-n^2}{2~n}\]

La courbe ci-contre a été tracée pour un verre d’indice \(n_1=1,51\). Soit : \[n=\frac{n_2}{n_1}=\frac{1}{1,51}=0,56\]

2.2. Parallélépipède de Fresnel

Reprenons la relation : \[\tan\frac{\varphi_m}{2}=\frac{1-n^2}{2~n}\]

On peut toujours faire en sorte que \(\varphi_m\) = 45 °. Il correspond 2 valeurs de \(n\), donc 2 valeurs de \(i_1\) (40 ° 37, 54 ° 37).

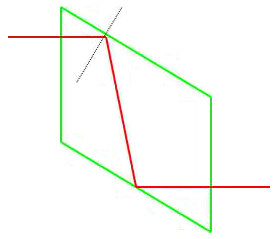Après deux réflexions totales, le déphasage entre la vibration parallèle et la vibration perpendiculaire sera \(\pi/2\).

Par exemple, si \(\overrightarrow{E_1}\) fait avec le plan d’incidence un angle de 45 °, on aura : \[E_1~\sin\theta=E_1~\sin\frac{\pi}{4}\quad\Rightarrow\quad E_{\parallel}=E_{\bot}\]

Les amplitudes sont donc égales.

À la sortie du parallélépipède, \(E_{\parallel}\) et \(E_{\bot}\) seront déphasées de \(\frac{\pi}{2}\). On aura ainsi réalisé une vibration circulaire.

Ce parallélépipède est désigné sous le nom de lame quart d’onde. En effet : \[\Delta\Phi=\frac{2~\pi}{\lambda}~\delta=\frac{\pi}{2}\quad\Rightarrow\quad\delta=\frac{\lambda}{4}\]

3. Incidence rasante et incidence normale

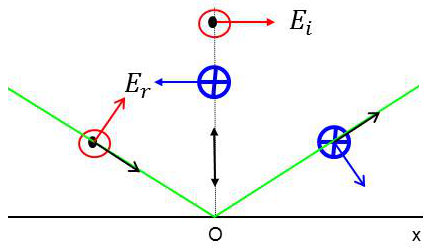a) Considérons d’abord le cas \(n_2>n_1\).

En incidence normale : \[r=\frac{n_1-n_2}{n_1+n_2}~<~0\]

La vibration se réfléchit en changeant de sens.

Pour étudier l’incidence rasante, on doit revenir aux courbes \(r_{\parallel}\) et \(r_{\bot}\) et chercher les valeurs pour \(i_1=\cfrac{\pi}{2}\). On a : \[r_{\bot}<0\quad\text{et}\quad r_{\parallel}>0\]

La vibration \(E_{\bot}\) change de sens ; pour \(E_{\parallel}\), on a la disposition de la figure ci-dessus : \[r_{\parallel}>0\qquad\text{signifie que :}\quad {\rm proj}_{ox}\overrightarrow{E_i}={\rm proj}_{ox}\overrightarrow{E_r}\]

b) Considérons à présent le cas \(n_2<n_1\).

En incidence normale : \[r=\frac{n_1-n_2}{n_1+n_2}~>~0\]

La vibration se réfléchit sans changer de sens.

Pour l’incidence rasante, on reprend une discussion analogue à la précédente à l’aide des courbes \(r_{\parallel}\) et \(r_{\bot}\).