1. Lignes neutres de la lame

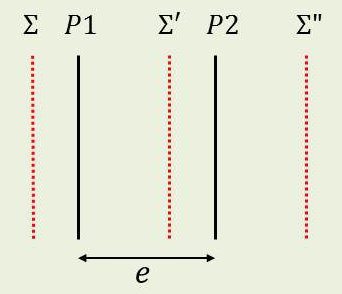Quand un plan d’onde \(\Sigma\) se présente parallèle aux faces d’une lame, il peut s’y propager sans altération.

L’une ou l’autre des deux directions privilégiées rectangulaires \(D_x\) et \(D_y\) peuvent être définies comme axes de section de l’ellipsoïde par ce plan.

Or, les vitesses de propagation de \(D_x\) et \(D_y\) sont différentes. Donc, les indices \(n_x\) et \(n_y\) correspondants sont différents.

Il en résulte une différence de marche : \[\delta=(n_y-n_x)~e\]

Si la lumière incidente est polarisée rectiligne avec ses vibrations parallèles à \(D_x\), alors les ondes transmises ne comportent que l’onde dont les vibrations sont parallèles à \(D_x\). La lame se comporte comme si elle n’était pas biréfringente et il en est de même si les vibrations incidentes sont parallèles à \(D_y\).

Les directions \(\overrightarrow{D_x}\) et \(\overrightarrow{D_y}\) s’appellent les lignes neutres de la lame. Les plans définis par ces directions et la normale à la lame s’appellent les sections principales.

Pour étudier la propagation d’une vibration quelconque de \(\Sigma\), nous la rapportons à deux axes rectangulaires \(O_x\) et \(O_y\) pris dans ce plan et parallèles respectivement à \(\overrightarrow{D_x}\) et \(\overrightarrow{D_y}\).

Si l’on suppose que \(n_y>n_x\) on a alors \(v_y<v_x\). L’axe \(Oy\) est alors dit axe lent de la lame.

2. Action sur une vibration rectiligne

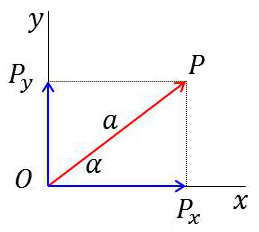Supposons que cette vibration ait pour amplitude \(a_0\) et qu’elle fasse un angle \(\alpha\) avec \(Ox\).

Après la traversée : \[\left\{ \begin{aligned} &x=a_0~\cos\alpha~\cos\omega~t=a~\cos\omega~t\\ &y=a_0~\sin\alpha~\cos\omega~t=b~\cos(\omega~t-\varphi) \end{aligned} \right.\] On sait que \(P_y\) est en retard sur \(P_x\) de : \[\varphi=\frac{2~\pi}{\lambda}~\delta=\frac{2~\pi}{\lambda}~(n_y-n_x)~e\]

Dans l’étude des vibrations, on a vu que la vibration résultante était elliptique, sauf pour certaines valeurs de \(\varphi\) pour laquelle elle était rectiligne.

2.1. Cas particuliers

1. \(\varphi=2~k~\pi\quad;\quad\delta=k~\lambda\)

   La vibration émergente est identique à la vibration incidente.
   Cette lame est dite lame onde.

2. \(\varphi=(2~k+1)~\pi\quad;\quad\delta=k~\lambda+\cfrac{\lambda}{2}\)

   La vibration émergente est rectiligne mais symétrique de la vibration incidente par rapport aux lignes neutres.
   Cette lame est dite demi-onde.

3. \(\varphi=(2~k+1)~\cfrac{\pi}{2}\quad;\quad\delta=k~\lambda+\cfrac{\lambda}{4}\)

   La vibration émergente est elliptique ; elle a pour axes les lignes neutres de la lame.
   Cette lame est dite quart d’onde.

Dans le cas particulier où \(\alpha\) = 45°, on a \(a\) = \(b\) : la vibration est alors circulaire.

2.2. Polariseur circulaire

Un polariseur suivi d’une lame \(\lambda/4\) dont les lignes sont à 45° de la direction de vibration constitue un polariseur circulaire. Sur la lumière circulaire obtenue, un analyseur simple n’a aucune action.

Il est intéressant de considérer le sens de rotation de cette vibration. \[\varphi=\frac{2~\pi}{\lambda}~\frac{\lambda}{4}=\frac{\pi}{2}\]

Par suite : \[\left\{ \begin{aligned} &x=a_0~\cos\omega~t\\ &y=a_0~\cos(\omega~t-\frac{\pi}{2}) \end{aligned} \right. \quad\text{remarquant que}\quad \left\{ \begin{aligned} &t=o~~;~~x=1~~;~~y=0\\ &t=\frac{T}{4}~~;~~x=0~~;~~y=1 \end{aligned} \right.\]

On remarque que la vibration circulaire est gauche. Si l’on avait changé \(Ox\) de sens (\(\varphi=-\pi/2\)), cette vibration aurait été droite.

Le sens de rotation est donc celui qui amène la vibration incidente sur l’axe lent par rotation inférieure à 90°.

On peut ainsi transformer un polariseur circulaire gauche en polariseur circulaire droit en tournant de 90° la lame \(\lambda/4\) par rapport au polariseur.

3. Action sur une vibration elliptique

Nous allons essentiellement examiner deux cas particuliers classiques.

3.1. Lame \(\lambda/2\)

Supposons la vibration elliptique rapportée aux axes \(xOy\) : \[(E)\qquad x=a~\cos\omega~t\quad;\quad y=b~\cos(\omega~t-\varphi)\]

La lame introduit une différence de marche \(\delta=\lambda/2\), donc un retard \(\psi=\pi\) de \(y\) sur \(x\). \[(E')\qquad x=a~\cos\omega~t\quad;\quad y=-b~\cos(\omega~t-\varphi)\]

L’ellipse \((E')\) représentée par ces équations est symétrique de l’ellipse incidente \((E)\) par rapport aux lignes neutres de la lame et elle est parcourue en sens inverse de la précédente.

3.2. Lame \(\lambda/4\)

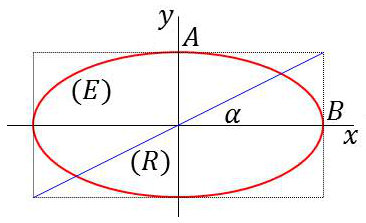Si on suppose les axes de l’ellipse confondus avec les lignes neutres, son équation est (en supposant l’ellipse droite) : \[x=A~\cos\omega~t\quad;\quad y=-B~\sin\omega~t\]

La lame \(\lambda/4\) introduit une autre différence de phase \(\pi/2\), la vibration \(y\) étant retardée.

La vibration émergente devient : \[x=A~\cos\omega~t\quad;\quad y=B~\cos\omega~t\]

On obtient donc une vibration rectiligne de pente \(\tan\alpha=B/A\). On remarquera que l’intensité a toujours pour valeur \(I=A^2+B^2\).

Le problème se complique un peu quand la vibration elliptique a une orientation quelconque. Pour le résoudre, on décompose la vibration en deux vibrations circulaires qui donnent dans la lame quart d’onde deux vibrations rectilignes rectangulaires. Il n’y a plus alors qu’à recomposer ces deux vibrations.

4. Compensateurs

On appelle compensateurs les dispositifs capables d’introduire, en un point donné du faisceau, une différence de marche donnée et variable à volonté.

4.1. Compensateur de Babinet

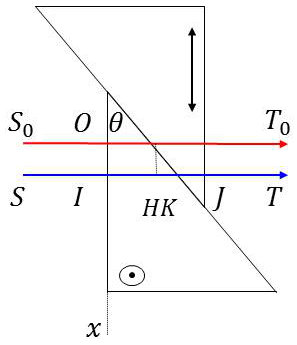Le compensateur de Babinet est formé de deux coins de quartz égaux. \(S_0OT_0\) est le rayon qui traverse les deux lames au point O où leurs épaisseurs sont égales. On choisit l’axe des abscisses comme indiqué sur la figure.

L’angle \(\theta\) étant petit, nous admettrons que les deux coins se comportent pour le rayon \(ST\) comme deux lames à faces parallèles d’épaisseur \([e=IK]\) et \([e'=KJ]\).

Comme \(HI=HJ\), on a donc : \[e-e'=2~HK=2~x~\tan\alpha\]

La première lame retarde la vibration parallèle à \(Oy\) et la seconde retarde la vibration parallèle à \(Ox\). Leurs actions sont de signes contraires et la différence de marche totale est : \[\delta=(n_y-n_x)~(e-e')=2~(n_y-n_x)~x~\tan\theta\]

4.2. Compensateur de Bravais

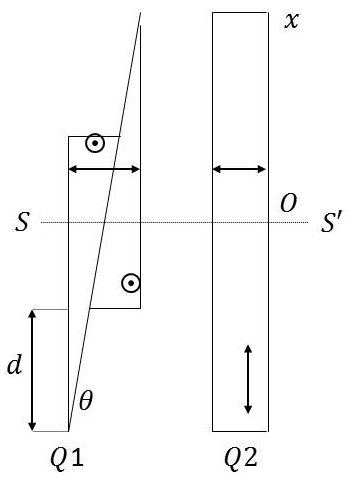Le compensateur de Bravais reprend le dispositif précédent, mais se compose de deux parties. Cette fois \(e' > e\).

On a : \[e'-e=d~\tan\theta\]

Donc, pour l’expression de la différence de marche : \[\delta=(n_y-n_x)~(e'-e)=(n_y-n_x)~d~\tan\theta\]

On remarquera cette fois que les axes optiques des deux moitiés de \(Q1\) sont les mêmes.

5. Analyse de la lumière

Examinons les différents types de lumière.

La lumière naturelle peut être décomposée en deux vibrations rectilignes rectangulaires, mais subissant des variations aléatoires : \[x=a_1~\cos(\omega~t-\psi_1)\quad;\quad y=a_2~\cos(\omega~t-\psi_2)\]

Les phases varient indépendamment l’une de l’autre et de façon quelconque.

La lumière polarisée rectiligne est telle que \(\overrightarrow{D}\) fait un angle constant \(\theta\) avec l’axe \(Ox\) ; les vibrations composantes sont en phase : \[x=a~\cos\theta~\cos(\omega~t-\psi)\quad;\quad x=a~\sin\theta~\cos(\omega~t-\psi)\]

Le terme de phase est même facultatif.

La lumière polarisée elliptique est telle que l’extrémité de \(\overrightarrow{D}\) décrive une ellipse dont l’équation paramétrique est : \[x=a~\cos\theta~\cos(\omega~t-\psi_1)\quad;\quad x=a~\sin\theta~\cos(\omega~t-\psi_2)\]

Toutefois, avec \(\psi_2-\psi_1=cte=\varphi\), on écrira de préférence : \[x=a~\cos\theta~\cos\omega~t\quad;\quad x=a~\sin\theta~\cos(\omega~t-\varphi)\]

5.1. Analyse d’une vibration rectiligne

5.1.1. Méthode d’extinction

Il faut parvenir à croiser la vibration et l’analyseur d’où la direction de la vibration qui est alors perpendiculaire à l’analyseur. Cependant, l’extinction n’est jamais absolue et l’œil doit rechercher un minimum, c’est à dire comparer entre eux des éclairements perçus successivement et non simultanément, en faisant appel à sa mémoire.

5.1.2. Méthode de l’analyseur à pénombre

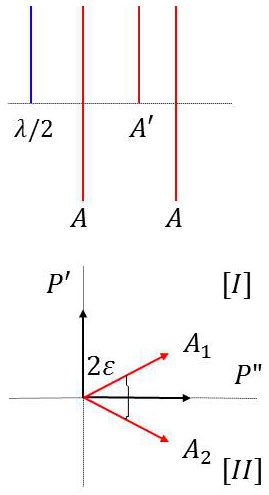Le champ observé est partagé en deux plages correspondant à deux directions d’analyse formant entre elles un petit angle \(2~\varepsilon\). Cela signifie que, dans la plage \([I]\), les vibrations sont éteintes si elles sont perpendiculaires à \(A_1\) et dans la plage \([II]\) si elles sont perpendiculaires à \(A_2\).

On peut obtenir ce résultat en plaçant devant un analyseur \(A\) une lame \(\lambda/2\) dont les lignes neutres font un angle \(\varepsilon\) avec l’azimut de vibration de \(A\). Dans la plage non couverte, \(A_1\) se confond avec \(A\). Dans la plage couverte, \(A_2\) à la direction \(A_1+2~\varepsilon\).

Ce dispositif n’est d’ailleurs valable que pour les radiations pour lesquelles la lame est vraiment demi-onde. On obtiendrait un même résultat (indépendamment de \(\lambda\)) en plaçant devant \(A\) un autre analyseur\(A'\) non absorbant, couvrant la moitié du champ et dont l’azimut fait l’angle \(2~\varepsilon\) avec celui de \(A\).

Cette séparation étant acquise avec l’un des deux procédés, les deux plages n’auront le même éclairement que si elles sont traversées par une vibration rectiligne dont la direction \(P\) fait un angle égal avec \(A\) et \(A'\), c’est-à-dire qu’elle est l’une des bissectrices \(P'\) ou \(P"\) de l’angle \((\overrightarrow{A_1},~\overrightarrow{A_2})\).

À la direction \(P"\) correspond dans les deux plages un éclairement : \[I_0~\cos^2\varepsilon\approx I_0\]

À la direction \(P'\) correspond l’éclairement : \[I_0~\sin^2~\varepsilon\approx I_0~\varepsilon^2\]

Dans ce deuxième cas, on dit que les deux plages sont dans le même état de pénombre. Toute variation de la direction de \(P\) à partir de \(P'\) ou \(P"\) provoque une différence dans l’éclairement des plages. Au voisinage de \(P"\) ce déséquilibre est très faible alors qu’il est important au voisinage de la position \(P'\) : c’est donc la disposition \(P'\) (pénombre) qu’il faut utiliser.

La sensibilité de cette méthode s’évalue facilement. Soit \(\beta\ll\alpha\), l’angle de \(P'\) et \(P"\).

Les éclairements respectifs sont : \[I_1=I_0~(\varepsilon+\beta)^2\quad;\quad I_2=I_0~(\varepsilon-\beta)^2\]

Le contraste vaut : \[\gamma=\frac{I_1-I_2}{(I_1+I_2)/2}\]

En négligeant les termes du second ordre : \[\gamma\approx\frac{4~\beta}{\varepsilon}\quad;\quad \varepsilon^2\gg\beta^2\]

Pour être perceptible, ce contraste doit être supérieur à \(\gamma_m\approx2~\%\). Il lui correspond sur le pointillé de l’azimut de \(P\) une incertitude : \[\beta_m=\frac{\gamma_m~\varepsilon}{4}=\frac{\varepsilon}{200}\]

Il s’agit donc d’une méthode précise. Elle est utilisée pour le polarimètre de Laurent dans la mesure de la rotation du plan de polarisation produite par certaines substances.

5.2. Analyse d’une vibration elliptique

5.2.1. Direction des axes

On sait qu’une vibration elliptique n’est transformée en vibration rectiligne par une lame \(\lambda/4\) que si ses axes sont confondus avec les lignes neutres de la lame.

Par double tâtonnement, on fait tourner indépendamment l’analyseur à pénombre et la lame \(\lambda/4\) jusqu’à ce qu’on arrive à une situation donnant l’égalité de pénombre : les axes de l’ellipse sont alors parallèles aux lignes neutres de la lame.

5.2.2. Rapport des axes

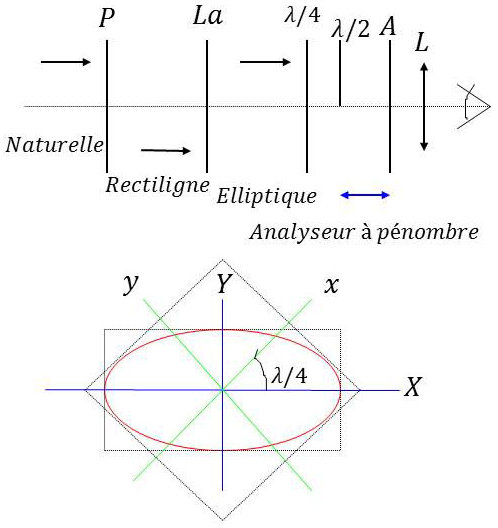La lumière naturelle, issue d’une source, traverse d’abord un prisme Nicols \(P\), puis la lame à étudier \(La\) dont les lignes neutres sont orientées à 45° de l’azimut du Nicols.

De la lame émerge une vibration elliptique dont un axe est l’azimut \(OX\) du Nicols. Les équations de \([E]\) dans le système \(xOy\) sont de la forme :

\[\begin{aligned} x&=a~\cos\omega~t\\ y&=a~\cos(\omega~t-\varphi)\\ \varphi&=\frac{2~\pi}{\lambda}~(n_y-n_x)~e\end{aligned}\]

Par changement d’axes :

\[\begin{aligned} X&=a~\big(\cos\frac{\varphi}{2}\big)~\cos\big(\omega~t-\frac{\varphi}{2}\big)\\ Y&=a~\big(\sin\frac{\varphi}{2}\big)~\sin\big(\omega~t-\frac{\varphi}{2}\big)\end{aligned}\]

Le rapport des axes de l’ellipse est donc : \[\tan\alpha=\frac{B}{A}=\tan\frac{\varphi}{2}\]

On sait déterminer \(\alpha\) ; on obtient alors \(\varphi\) et par suite la biréfringence \((n_y-n_x)\).

6. Interférences en lumière polarisée

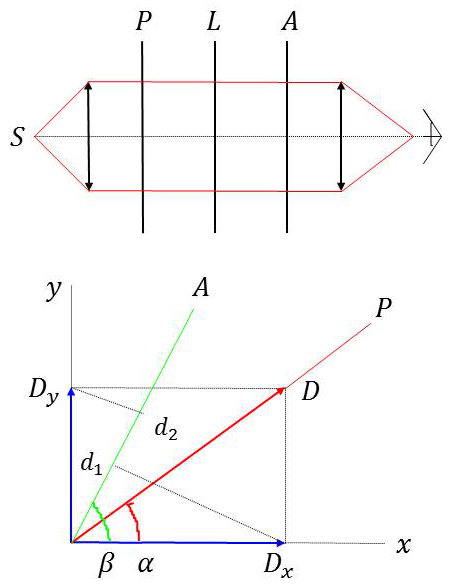La lame à étudier est placée entre polariseur et analyseur dont les azimuts font respectivement les angles \(\alpha\) et \(\beta\) avec l’axe \(Ox\) de la lame. Le tout est éclairé en lumière blanche.

Le polariseur capte \(\overrightarrow{D}\) que l’on décompose en \(\overrightarrow{D_x}\) et \(\overrightarrow{D_y}\) suivant les lignes neutres de la lame.

Entre \(\overrightarrow{D_x}\) et \(\overrightarrow{D_y}\), on sait qu’il existe un déphasage : \[\varphi=\frac{2~\pi}{\lambda}~(n_y-n_x)~e\]

Enfin, l’analyseur ne laisse passer que les vibrations qui lui sont parallèles, donc les projections de \(\overrightarrow{D_x}\) et \(\overrightarrow{D_y}\) sur \(A\).

On est ainsi conduit à un phénomène d’interférences à deux ondes :

\[\begin{aligned} &D_x=D~\cos\alpha~\cos\omega~t\\ &D_y=D~\sin\alpha~\cos(\omega~t-\varphi)\end{aligned}\]

En projection sur l’analyseur :

\[\begin{aligned} &(D_x)_A=D~\cos\beta~\cos\alpha~\cos\omega~t\\ &(D_y)_A=D~\sin\beta~\sin\alpha~\cos(\omega~t-\varphi)\end{aligned}\]

Les amplitudes respectives seront :

\[\begin{aligned} &d_1=D~\cos\beta~\cos\alpha\\ &d_2=D~\sin\beta~\sin\alpha\end{aligned}\]

La vibration résultante portée par \(A\) sera : \[S=D~\cos\omega~t~\{\cos\alpha~\cos\beta+\sin\alpha~\sin\beta~\cos\varphi\}+ D~\sin\omega~t~\{\sin\alpha~\sin\beta~\sin\varphi\}\]

On a alors (rapport d’intensités) : \[\frac{I}{I_A}=\{1\}^2+\{2\}^2=\cos^2\alpha~\cos^2\beta+\sin^2\alpha~\sin^2\beta+2\cos\alpha~\cos\beta~\sin\alpha~\sin\beta~\cos\varphi\]

Résultat qui peut s’exprimer sous deux formes :

\[\begin{aligned} &[1]\qquad I=I_A~\big\{\cos^2(\beta-\alpha)-\sin 2~\alpha~\sin 2~\beta~\sin^2\frac{\varphi}{2}\big\}\\ &[2]\qquad I=I_A~\big\{\cos^2(\beta+\alpha)+\sin 2~\alpha~\sin 2~\beta~\sin^2\frac{\varphi}{2}\big\}\end{aligned}\]

Premier cas : \(\alpha\) et \(\beta\) appartiennent au même quadrant, par exemple :\(\qquad\qquad\)

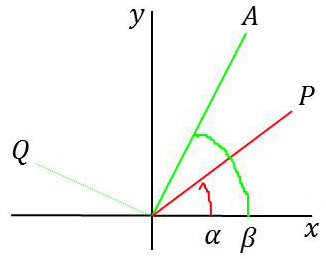\[\alpha<\frac{\pi}{2}~~;~~\beta<\frac{\pi}{2}\quad\Rightarrow\quad\sin 2~\alpha~\sin 2~\beta~>~0\]

D’après \([1]\), on aura \(I_{max}\) pour :

\[\begin{aligned} \cos^2\frac{\varphi}{2}=1\quad&\Rightarrow\quad\varphi=2~k~\pi\quad~\quad\quad\Rightarrow\quad\delta=k~\lambda\\ \cos^2\frac{\varphi}{2}=0\quad&\Rightarrow\quad\varphi=(2~k+1)~\pi\quad\Rightarrow\quad\delta=(2~k+1)~\frac{\lambda}{2}\end{aligned}\]

On obtient donc un spectre cannelé dont les franges occupent la même place que les franges d’interférence en lumière naturelle.

Comme : \(I_{min}=I_0~\cos^2(\beta+\alpha)\), on voit que les franges ne seront complètement noires que si l’on a : \[\alpha+\beta=\frac{\pi}{2}~~\text{ou}~~\frac{3~\pi}{2}\qquad\text{c'est-à-dire :}\quad\beta=(\pi-\alpha)\pm\frac{\pi}{2}\]

Ce qui se produit quand l’analyseur \(OA\) est perpendiculaire à la direction \(OQ\) symétrique de \(OP\) par rapport à \(Oy\).

Deuxième cas : \(\alpha\) et \(\beta\) n’appartiennent pas au même quadrant (\(\sin 2~\alpha~\sin 2~\beta~<~0\)).

\([2]\) est alors utilisée et la discussion est analogue à la précédente.

L’éclairement des franges sombres est donné par : \[I_{min}=I_0~\cos^2(\beta-\alpha)\]

Il est nul pour \(\beta-\alpha=\pm\cfrac{\pi}{2}\), c’est-à-dire quand l’analyseur \(OA\) et le polariseur \(OP\) sont croisés.

En outre, si on veut que les franges lumineuses soient les plus nettes possibles il faut que l’on ait, de plus : \[|\sin 2~\alpha|=|\sin 2~\beta|=1\]

Soit : \[\alpha=\frac{\pi}{4}~~\text{ou}~~\frac{3~\pi}{4}\quad;\quad\beta=\frac{\pi}{4}~~\text{ou}~~\frac{3~\pi}{4}\]

Conditions que l’on doit associer à : \[\beta=(\pi-\alpha)\pm\frac{\pi}{2}\quad\text{ou}\quad\beta-\alpha=\pm\frac{\pi}{2}\]

Ainsi, le système a la visibilité maximale entre Nicols croisés ou parallèles disposés à 45° des tourmalines.

En résumé

Pour obtenir un spectre cannelé aussi visible (cannelures sombres entièrement noires) et aussi brillant (cannelures brillantes d’éclairement maximal) que possible, il faut placer la lame cristalline entre Nicols croisés ou parallèles, ses sections principales faisant un angle de 45° avec celles des Nicols.

La répartition des éclairements est alors donnée par :

Nicols croisés : \[I_1=I_{\lambda}~\sin^2\frac{\varphi}{2}=I_{\lambda}~\sin^2\frac{\pi~\delta}{\lambda}\]

Nicols parallèles : \[I_1=I_{\lambda}~\cos^2\frac{\varphi}{2}=I_{\lambda}~\cos^2\frac{\pi~\delta}{\lambda}\]

Les deux spectres cannelés obtenus sont complémentaires, c’est-à-dire que la somme des éclairements \(I_1+I_2\) qui correspondent à une longueur d’onde quelconque est égale à l’éclairement \(I_{\lambda}\) qui lui correspond dans le spectre obtenu en enlevant l’analyseur.

Quelles que soient les positions des Nicols et de la lame, on remplace toujours le spectre complémentaire en tournant l’analyseur de 90°, comme on le vérifiera en faisant la somme des éclairements qui correspondent aux angles \(\beta\) et \(\beta+\cfrac{\pi}{2}\) :

\[\begin{aligned} &I_1=I_{\lambda}~\big\{\cos^2(\beta-\alpha)-\sin 2~\alpha~\sin 2~\beta~\sin^2\frac{\varphi}{2}\big\}\\ &I_2=I_{\lambda}~\big\{\cos^2(\beta-\alpha+\frac{\pi}{2})-\sin 2~\alpha~\sin 2~(\beta+\frac{\pi}{2})~\sin^2\frac{\varphi}{2}\big\}\end{aligned}\]