1. Généralités
Nous entendons, par milieu linéaire, un milieu cylindrique dans lequel tous les points d’une même section droite subissent à chaque instant un mouvement identique ; le milieu propage alors une onde plane dont les plans d’onde coïncident avec les sections droites.
Un point (ou ce qui revient au même, une section droite) du milieu linéaire sera défini par l’abscisse \(x\) qu’il a au repos, en l’absence de vibration. Cette abscisse permet donc de repérer le point matériel considéré sur la section.
Le point d’abscisse \(x\) au repos est au cours du temps le siège d’une oscillation représentée par la variable \(y\) qui se trouve ainsi fonction du temps et du point choisi, c’est-à-dire des deux variables \(x,~t\). Nous trouvons alors que l’équation qui régit les petits mouvements de l’ensemble est une équation aux dérivées partielles du second ordre : \[\frac{\partial^2y}{\partial t^2}=c^2~\frac{\partial^2y}{\partial x^2}\]
dont la solution la plus générale : \[y=f\Big(t-\frac{x}{c}\Big)+g\Big(t+\frac{x}{c}\Big)\]
représente l’état le plus général de vibrations dans le milieu linéaire continu et indéfini dans les deux sens.
Les fonctions \(f\) et \(g\) sont des fonctions quelconques et l’état de vibration le plus général est donc représentable par la superposition de deux ondes de déformation se déplaçant à la même vitesse dans des directions opposées et de forme quelconque. La valeur \(c\) est souvent désignée sous le nom de célérité de l’onde.
En effet, le milieu étant indéfini et excité pour fixer les idées à gauche de l’observateur (du côté des \(x\) négatifs), le milieu placé à droite de l’observateur est, comme nous le verrons, soumis à la seule onde de déformation \(f\). Il est évident que, dans ces conditions, que l’état de vibration observé en \(x\) à l’instant \(t\), se retrouve identique, à l’instant \(t+\theta\) au point \(x+c~\theta\) (rappelons que \(x\) représente l’abscisse de repos).
Si le milieu se termine par contre en un certain plan vers la droite, l’onde de déformation \(f\) va en général se réfléchir en ce point et donner naissance à une onde de type \(g\) se propageant vers la gauche ; nous serons alors obligés de considérer l’ensemble des deux fonctions \(f,~g\) pour représenter l’état de mouvement.
Une onde du type \(f\) (ou du type \(g\)) constitue une onde progressive qui propage de l’énergie tout au long du milieu linéaire. La superposition des deux types ne constitue plus une onde progressive : il peut arriver que la superposition des deux ondes constitue par contre une onde stationnaire qui ne correspond plus à une propagation d’énergie dans un sens ou dans l’autre, chacun des éléments du milieu linéaire conservant une énergie moyenne constante au cours du temps.
2. Propagation d’un ébranlement d’ondes planes dans un tuyau
Considérons un tuyau cylindrique à parois indéformables, illimité dans les deux sens et empli d’un fluide (gaz ou liquide) dont la pression au repos est \(P_0\) et dont la masse spécifique au repos est \(\rho\).
 Supposons qu’à un instant donné un ébranlement soit communiqué à une certaine section du fluide, élevant localement la pression \(P_0~\rightarrow~P_0+\delta P\), c’est-à-dire faisant apparaître une petite surpression locale \(\delta P\) en cette section.
Supposons qu’à un instant donné un ébranlement soit communiqué à une certaine section du fluide, élevant localement la pression \(P_0~\rightarrow~P_0+\delta P\), c’est-à-dire faisant apparaître une petite surpression locale \(\delta P\) en cette section.
Cette surpression repousse légèrement les tranches de fluide voisines qui se trouvent elles-mêmes comprimées et repoussent les tranches ultérieures. D’où une propagation de l’ébranlement dans les deux directions à partir de la section initialement perturbée. C’est cette propagation que nous nous proposons d’étudier.
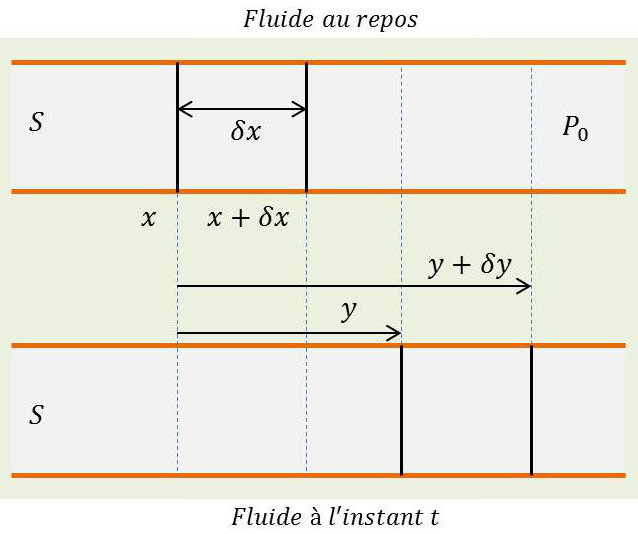
Au cours du mouvement, les diverses sections du fluide (tranches infiniment minces découpées suivant une section droite) se trouvent déplacées par rapport à leur position au repos. L’abscisse au repos d’une section donnée était \(x\). Son abscisse réelle à l’instant \(t\) est \(x’=x+y\). C’est la quantité \(y\) que nous choisissons pour définir le déplacement de la section considérée.
\(y\) est fonction du temps \(t\) et de la quantité \(x\) qui caractérise la tranche infiniment mince de fluide que nous avons choisie. Insistons sur ce fait que \(x\), abscisse au repos, reste évidemment invariable pour une tranche de fluide donnée. Faire varier \(x\) revient à considérer successivement des tranches de fluide différentes.
Une tranche de fluide indéfiniment mince verra sa position définie par son déplacement \(y\). Nous définirons également son état par sa surpression à l’instant \(t\) considéré, c’est-à-dire par l’excès (positif ou négatif) de pression qui règne à l’instant \(t\) en cette section par rapport à la pression au repos \(P_0\).
Considérons alors deux sections de fluide voisines d’abscisses au repos \(x\) et \(x+\delta x\). Si \(S\) est la section du tuyau, la masse de fluide comprise entre ces deux sections est exactement \(\rho~S~\delta x\), \(\rho\) étant la masse spécifique au repos et \(\delta x\) la longueur au repos de la tranche de fluide considérée.
À l’instant \(t\), les abscisses réelles des sections limitant cette tranche de fluide sont \(x+y\) et \(x+\delta x+y+\delta y\) . La tranche de fluide considérée a donc subi depuis le repos un allongement algébrique égal à \(\delta y\), soit une variation de volume (la section \(S\) étant maintenue constante dans le tuyau) : \(\delta V=S~\delta y\).
Introduisons la variation relative de volume ou dilatation \(\theta\) subie par la tranche de fluide entre l’état de repos et l’instant considéré. Cette variation de volume est : \[\theta=\frac{\delta y}{\delta x}\]
Si nous nous limitons à de petits déplacements et, par suite, à de petites dilatations et surpressions, nous pourrons confondre ce rapport avec la dérivée par rapport à \(x\), à l’instant \(t\), de la fonction \(y(x,~t)\) qui caractérise le déplacement, soit : \[\theta=\frac{\partial y}{\partial x}\]
Or, toute dilatation du fluide implique une variation de pression. Introduisons le coefficient de compressibilité du fluide (coefficient de compressibilité adiabatique) : \[\chi=-\frac{1}{v}~\frac{\delta v}{\delta p}\]
Nous en déduisons que la surpression locale est liée à la dilatation par la relation très simple : \[\delta p=-\frac{\theta}{\chi}\]
Comme la surpression \(\delta p\) et le déplacement \(y\), la dilatation est bien entendu fonction de \(x\) et de \(t\). Remarquons en outre que la vitesse et l’accélération à l’instant \(t\) de la tranche d’abscisse \(x\) au repos sont données par les expressions : \[u(x,~t)=\frac{\partial y}{\partial t}\quad;\quad \gamma(x,~t)=\frac{\partial^2 y}{\partial t^2}\]
Ceci puisque \(y\) constitue la seule partie variable de l’abscisse réelle de la tranche de fluide à l’instant \(t\).
2.1. Équation de propagation des ondes planes
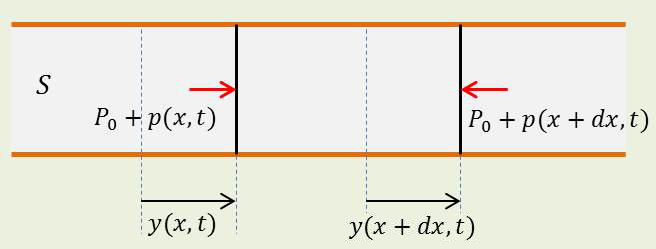 Considérons alors une tranche de fluide comprise entre les sections d’abscisses au repos \(x\) et \(x+\delta x\) et, par suite, de masse \(\rho~S~\delta x\) et appliquons au mouvement de cette tranche de fluide le théorème fondamental de la dynamique.
Considérons alors une tranche de fluide comprise entre les sections d’abscisses au repos \(x\) et \(x+\delta x\) et, par suite, de masse \(\rho~S~\delta x\) et appliquons au mouvement de cette tranche de fluide le théorème fondamental de la dynamique.
La tranche de fluide est soumise aux deux forces suivantes (comptées positivement dans le sens \(Ox\)):
-
sur la face gauche, à la force : \(\quad S\{P_0+\delta p(x)\}\) ;
-
sur la face droite, à la force : \(~~\quad S\{P_0+\delta p(x+\delta x)\}\).
Elle est donc soumise au total à la force : \[S\{\delta p(x)-\delta p(x+dx\}=-S~\frac{\partial(\delta p)}{\partial x}\qquad\text{au second ordre près.}\]
Elle prend de ce fait une accélération : \[\gamma=\frac{\partial u}{\partial t}=\frac{\partial^2y}{\partial t^2}\]
telle que : \[\rho~S~dx~\frac{\partial^2y}{\partial t^2}=-S~dx~\frac{\partial(\delta p)}{\partial x}\]
D’où une première relation exprimant l’inertie de la tranche de fluide : \[\rho~\frac{\partial^2y}{\partial t^2}=-\frac{\partial(\delta p)}{\partial x}\]
Combinons-la avec la relation : \[\delta p=-\frac{\theta}{\chi}=-\frac{1}{\chi}~\frac{\partial y}{\partial x}\]
Elle exprime l’élasticité de la tranche de fluide ; et nous obtenons : \[\frac{\partial^2y}{\partial t^2}=\frac{1}{\rho~\chi}~\frac{\partial^2y}{\partial x^2}\]
Introduisant la quantité : \[c=\frac{1}{\sqrt{\rho~\chi}}\]
qui est une constante caractéristique du fluide considéré et de ses conditions physiques (pression et température au repos) : \[\frac{\partial^2y}{\partial t^2}=c^2~\frac{\partial^2y}{\partial x^2}\]
Cette équation aux dérivées partielles du second ordre constitue l’équation de propagation des ondes planes dans le fluide.
La solution générale de cette équation aux dérivées partielles est représentée par la somme de deux fonctions arbitraires des arguments respectifs : \[y=f\Big(t-\frac{x}{c}\Big)+g\Big(t+\frac{x}{c}\Big)\]
On peut en effet vérifier immédiatement qu’une fonction \(y(x,~t)\) ayant cette forme est solution de l’équation de propagation ; nous admettrons que, réciproquement, toute solution de l’équation de propagation peut être mise sous cette forme.
L’état de mouvement le plus général au sein du fluide contenu dans le tuyau (rappelons que nous ne considérons que les mouvements d’ensemble des diverses actions du fluide se déplaçant parallèlement à \(Ox\)) peut donc être représenté par la superposition de deux ondes de compression (ou dilatation).
L’une se déplace dans le sens des \(x\) positifs à la vitesse \(c\) (cette onde étant représentée par la loi de déplacement \(y=f(t-x/c)\), l’autre dans le sens opposé à la même vitesse (cette onde étant représentée par la loi de déplacement \(g(t-x/c)\).
On peut s’arranger pour qu’une seule des ondes apparaisse dans la région du tuyau que l’on considère. Fermons à gauche le tuyau par un piston coulissant sans frottement. De l’autre côté du piston se trouve par exemple un espace vide de tout gaz à l’intérieur duquel un ressort de grande longueur exerce sur le piston un effort pratiquement indépendant de sa position et qui équilibre la pression au repos \(P_0\).
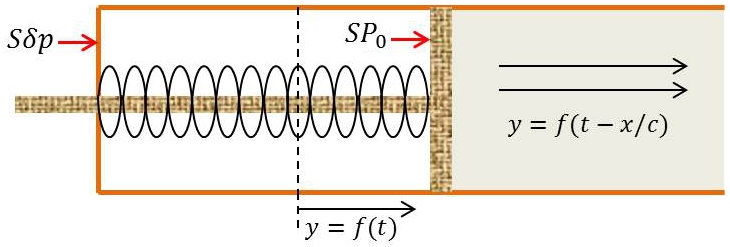 Le tuyau est illimité vers la droite (ceci ne semble pas très pratique, mais nous verrons plus loin qu’un freinage convenable du fluide à l’extrémité de droite permet de réaliser les conditions du tuyau illimité).
Le tuyau est illimité vers la droite (ceci ne semble pas très pratique, mais nous verrons plus loin qu’un freinage convenable du fluide à l’extrémité de droite permet de réaliser les conditions du tuyau illimité).
Imprimons au piston une loi de déplacement quelconque au cours du temps (déplacement de petite amplitude). Un ébranlement en résulte, qui se propage nécessairement vers la droite et s’éloigne indéfiniment. Aucune discontinuité située vers la droite ne réfléchissant l’ébranlement, le mouvement du fluide est représenté par la seule onde progressive \(y=f(t-x/c)\).
La forme de la fonction \(f\) est précisément celle de la fonction \(f(t)\) qui représente le mouvement du piston (celui-ci se trouve constamment au contact de la tranche de fluide d’abscisse 0 au repos).
Une onde de type \(g\) serait évidemment obtenue en plaçant le piston à droite et en supposant le tuyau illimité vers la gauche.
2.2. Propriété de l’onde progressive
Supposons donc que le mouvement du fluide soit représenté par la seule onde progressive \(f(t-x/c)\) .
L’état du fluide à l’instant \(t\) et en la section d’abscisse \(x\) au repos se retrouve identique à l’instant \(t'\) en la section d’abscisse au repos \(x=c~(t-t')\). Si, par exemple, le piston a effectué un aller-retour pendant un intervalle de temps \(\theta\), une tranche de fluide d’épaisseur \(c~\theta\) se trouve comprimée (ou dilatée) et ses frontières se propagent toutes deux à la vitesse \(c\) vers les \(x\) positifs.
La loi de distribution des pressions, des déplacements, etc. à l’intérieur de cette tranche de fluide reste invariable et il semble que ce soit la tranche de fluide elle-même qui se déplace dans le tuyau. En fait, bien entendu, les molécules de fluide restent au voisinage de leur position initiale et ce n’est que le mouvement qui se propage d’une tranche à l’autre.
Il en est de même pour les vagues qui semblent avancer sur un océan. Les molécules d’eau ne subissent en gros que des mouvements verticaux et un flotteur disposé sur l’eau reste à distance fixe de la côte, bien que la masse d’eau semble avancer au-dessous de lui.
De l’expression du déplacement, nous tirerons immédiatement les expressions de la vitesse de la tranche du fluide, de la dilatation et de la surpression sous la forme :
\[\begin{aligned} u&=\frac{\partial y}{\partial t}=f'\Big(t-\frac{x}{c}\Big)\\ \theta&=\frac{\partial y}{\partial x}=-\frac{1}{c}~f'\Big(t-\frac{x}{c}\Big)\\ \delta p&=-\frac{\theta}{\chi}=\frac{1}{\chi~c}~f'\Big(t-\frac{x}{c}\Big)=\rho~c~f'\Big(t-\frac{x}{c}\Big)\end{aligned}\]
Nous remarquons que, quelle que soit la forme de la fonction \(f\), il existe entre la vitesse de la tranche de fluide, sa dilatation et sa surpression au même instant des rapports constants, c’est-à-dire indépendants de la section considérée et de l’instant considéré.
On a comme coutume de désigner sous le nom de résistivité acoustique le rapport constant qui existe entre la surpression et la vitesse locales au sein du fluide traversé par l’onde progressive \(f\) et de forme quelconque, soit : \[\frac{\delta p}{u}=\rho~c=\mathcal{R}=\text{cte}\]
On a coutume de désigner sous le nom de résistance acoustique du tuyau rempli de fluide le quotient : \[R=\frac{\rho c}{S}\]
qui représente le rapport constant entre la surpression \(\delta p\) et le débit instantané \(S.u\) : \[\frac{\delta p}{S~u}=\text{cte}=R=\frac{\mathcal{R}}{S}=\frac{\rho~c}{S}\]
Des résultats tout à fait analogues seraient bien entendu obtenus pour une onde progressive se dirigeant vers la gauche. Il suffit de considérer cette onde comme se propageant vers la droite à la vitesse négative \((-c)\), pour vérifier qu’il existe un rapport \(\mathcal{R}=\rho~c\) entre la surpression et la vitesse locales, et un rapport constant \(R=\rho~c/S\) entre la surpression et le débit, lorsque l’onde progressive considérée se propage vers les \(x\) négatifs.
Toutefois, si nous considérons le mouvement le plus général résultant de la superposition des deux ondes, cette propriété disparaît et le rapport surpression / vitesse dépend, en général, non seulement de l’abscisse au repos de la section, mais encore du temps. Nous y reviendrons.
2.3. Cas particulier d’une excitation sinusoïdale
Soit \(f(t)=a~\cos\omega~t\) la loi de déplacement du piston en contact avec la tranche de fluide d’abscisse \(x=0\) au repos.
La tranche de fluide au repos \(x\) a, à l’instant \(t\) :
-
un déplacement : \(~y=a~\cos\Big(\omega~t-\frac{x}{c}\Big)\)
-
une vitesse : \(u=-a~\omega~\sin\Big(\omega~t-\frac{x}{c}\Big)\)
-
une surpression : \(\delta p=-\rho~c~a~\omega~\sin\Big(\omega~t-\frac{x}{c}\Big)\)
On retrouve à chaque point le même déplacement, la même surpression, etc., à des intervalles de temps égaux à \(T=\cfrac{2~\pi}{\omega}\).
On retrouve à chaque instant les mêmes surpressions, déplacements, etc., en des sections dont la distance, comptée dans le fluide au repos, est égale à une longueur d’onde : \[\lambda=c~T=\frac{2~\pi~c}{\omega}\]
Le déplacement à partir du repos étant le même en ces diverses sections, la distance réelle de ces diverses sections est, elle aussi, égale à la longueur d’onde \(\lambda\). La longueur d’onde \(\lambda\) constitue la période spatiale de l’onde comme \(T\) constitue sa période dans le temps.
Tout ébranlement peut être décomposé en une infinité d’ébranlements sinusoïdaux. Si l’ébranlement est périodique et de période \(T\), les ébranlements sont de période \(T/2,~\dots,~T/n\).
Si, comme nous l’avons supposé implicitement jusqu’à présent, la célérité est indépendante de la fréquence, c’est-à-dire s’il n’y a pas dispersion, l’ébranlement se transporte en bloc à la vitesse \(c\) ainsi que l’a montré notre théorie élémentaire. Si \(c\) dépend de la fréquence, par contre, les diverses composantes sinusoïdales se déphasent progressivement lors de la propagation et il y a déformation du signal au cours de la propagation.
Jusqu’à nouvel ordre, nous supposerons qu’il n’y a pas dispersion, et considèrerons \(c\) comme une constante, la nature du fluide étant déterminée ainsi que son état de repos.
2.4. Puissance instantanée transmise sur une section
Au travers d’une section quelconque, le fluide situé à gauche de la section exerce sur le fluide situé à droite un effort de pression égal à \(S~(P_0+\delta p)\) dont le travail pour un déplacement \(dy\) de la section est égal à : \[dW_0=S~dy~(P_0+\delta p)\]
Le travail total exercé au travers de cette section (sur le fluide situé à droite) lors du passage d’un ébranlement à la fin duquel le fluide retrouve sa position de repos est égal à : \[W_0=S~P_0\int y+S\int \delta p~\delta y\]
La première intégrale est nulle, le fluide ayant retrouvé en définitive sa position de repos, et le travail total se réduit à celui de la force de surpression \(S~\delta p\).
De la même façon, si l’on considère la valeur moyenne de la puissance \(P\) développée par la force pendant un temps très long au cours duquel le fluide ne s’écarte pas de façon importante de sa position de repos, cette valeur \(P\) s’identifie avec la valeur moyenne de la puissance développée par la seule force de surpression \(S~\delta p\).
C’est donc cette seule force de surpression que nous sommes amenés à retenir pour calculer la puissance transportée par l’onde au travers de la section considérée (et ceci bien que la majeure partie de l’effort exercé sur la portion de gauche du fluide sur la portion de droite soit constituée par la quantité \(S~P_0\)).
La section se déplaçant pendant le temps \(dt\) de la quantité \(u~dt\), la puissance instantanée transmise au travers de la section (étant sous-entendu qu’il s’agit de la puissance fournie par la seule surpression) est : \[P(x,~t)=S~\delta P(x,~t)~u(x,~t)=R~(S~u)^2\]
Le débit étant analogue à une intensité de courant, l’analogie avec le cas d’une résistance électrique est évidente. En particulier, dans le cas d’une oscillation sinusoïdale où la vitesse en tout point varie selon la loi : \[u=u_0~\cos\omega\Big(t-\frac{r}{c}\Big)\]
La puissance moyenne transmise au travers d’une section quelconque est la même pour toutes les sections et a la valeur : \[\overline{P}=R~S^2~u^2=R~S^2~\frac{u_0^2}{2}\]
La puissance moyenne transmise par unité de section constitue l’intensité de l’onde sinusoïdale. Elle a pour valeur : \[\frac{R}{2}~S~u_0^2=\frac{\mathcal{R}}{2}~u_0^2=\frac{\rho~c}{2}~u_0^2\]
2.5. Énergies potentielle et cinétique dans une tranche de fluide
Soit une tranche de fluide dont la surpression est \(\delta p\). Cette tranche de fluide, maintenue entre deux cloisons mobiles au sein de l’ensemble du fluide de pression uniforme \(P_0\), serait capable de fournir un certain travail en repoussant les cloisons qui l’enferment jusqu’à ce qu’elle ait atteint la pression \(P_0\).
Le volume au repos de la tranche de fluide étant \(\delta v\) et sa dilatation \(\theta=-\chi~\delta p\), le travail qu’elle fournit lorsque sa dilatation passe de \(\theta\) à \(\theta+\delta\theta\) est : \[dW_0=-(P_0+\delta p)~\delta v~\delta\theta\]
Or, la majeure partie de ce travail est fournie au fluide (ou, si l’on veut, aux deux pistons qui limitent à droite et à gauche la colonne de fluide) et le travail recueilli par l’opérateur qui maintient les cloisons mobiles se réduit à : \[\delta W=-\delta p~\delta v~\delta\theta=+\frac{1}{\chi}~\theta~\delta\theta~\delta v\]
La dilatation passant de \(q\) à \(0\), le travail total recueilli par les cloisons est : \[dW=\frac{\theta^2}{2~\chi}~\delta v=\chi~\frac{(\delta p)^2}{2}~\delta v\]
On a coutume de désigner sous le nom d’énergie potentielle de l’élément de fluide \(\delta v\) soumis à la surpression \(\delta p\) le travail qu’il est ainsi possible de recueillir sur les cloisons mobiles lorsque l’élément \(\delta v\) plongé dans le fluide retourne à la pression statique \(P_0\).
Notons que cette définition est assez artificielle et ne correspond pas, par exemple, à l’accroissement d’énergie interne du fluide à partir du repos (qui est de l’ordre de \(P_0.\theta.\delta v\) et est, par suite, beaucoup plus grand).
Mais si nous prenons la valeur moyenne de cet accroissement d’énergie interne, au cours d’une oscillation sinusoïdale par exemple, la valeur moyenne du terme \(P_0~\theta~\delta v\) dû à la pression de repos est nulle, de sorte que la valeur moyenne de l’énergie interne s’identifie à la valeur moyenne de l’énergie potentielle calculée à partir de la seule surpression.
Il en résulte que le fluide soumis à la surpression \(\delta p\) (et par suite à la dilatation \(\theta\)) renferme par unité de volume un contenu d’énergie potentielle : \[E_p=\frac{\chi}{2}~(\delta p)^2=\frac{\theta^2}{2~\chi}\]
On la désigne sous le nom de densité d’énergie potentielle au point où la surpression est \(\delta p\). En outre, l’élément \(dv\) lancé à la vitesse \(u\) possède un contenu d’énergie cinétique : \[dE_c=\frac{\rho}{2}~u^2~dv\]
D’où une densité d’énergie cinétique au point où la vitesse est \(u\) : \[E_c=\frac{\rho}{2}^2\]
Supposons le fluide traversé par une onde progressive, on a dans ce cas : \[(\delta p)^2=(\rho~c)^2~u^2\]
Et par suite : \[E_p=\frac{\chi}{2}~(\rho~c)^2~u^2=\frac{\rho}{2}~u^2=E_c\qquad\text{puisque :}\quad\rho~c^2=\frac{1}{\chi}\]
La densité d’énergie potentielle est donc, lorsque le fluide est traversé par une onde progressive, égale en tout point à la densité d’énergie cinétique. Leur somme constitue la densité d’énergie vibratoire : \[E=E_p+E_c=2~E_0=\rho~u^2\]
Cette énergie se transporte le long du tuyau (comme la vitesse \(u\), la surpression et le déplacement) à la vitesse \(c\) ; l’énergie qui traverse pendant le temps \(dt\) une section donnée est donc égale à \(c~E~dt\) , d’où une puissance instantanée transmise à travers la section : \[P=c~E=\rho~c~u^2\qquad\text{résultat déjà obtenu.}\]
3. Vibration longitudinale au sein d’une barre rigide
Une étude tout-à-fait analogue permettrait d’établir l’équation de propagation des vibrations longitudinales au sein d’une barre rigide, c’est-à-dire des vibrations dans lesquelles l’ensemble d’une section droite se déplace sans déformation dans le sens des génératrices de la barre cylindrique.
La seule modification à apporter aux formules consiste à remplacer le coefficient de compressibilité par la quantité \(1/E\) (E étant le module d’élasticité, cf. suite de l’article).
L’équation de propagation des ondes planes au long de la barre est : \[\frac{\partial^2y}{\partial t^2}=\frac{E}{\rho}~\frac{\partial^2y}{\partial x^2}= c^2~\frac{\partial^2y}{\partial x^2}\quad;\quad c=\sqrt{\frac{E}{\rho}}\qquad\text{célérité des ondes}\]
Une différence se présente cependant avec le cas des fluides que nous avons étudiés précédemment. Les fluides étaient enfermés dans un tuyau indéformable alors que la barre solide est bien entendu libre de subir des contractions et des dilatations latérales lors du passage de l’onde.
Si ces contractions et dilatations latérales étaient interdites à la barre solide, un effort plus grand serait nécessaire pour un allongement donné, d’où un module d’élasticité plus grand et une célérité des ondes plus élevée. Il semble difficile de trouver une enveloppe assez rigide pour empêcher les contractions et dilatations latérales d’une barre d’acier par exemple.
Si nous considérons des ondes planes longitudinales se propageant dans un milieu solide indéfiniment étendu dans toutes les directions (c’est-à-dire en pratique dont toutes les dimensions sont grandes devant la longueur d’onde), un cylindre de matière découpé dans la partie centrale et de génératrices parallèles à la direction de propagation se comportera exactement comme une barre solide dont les déformations latérales sont interdites.
Un effort de compression voit en effet sa composante latérale exactement compensée par la compression des parties avoisinantes situées dans le même plan d’onde.
Dans le cas des fluides, par contre, la célérité des ondes planes est la même, qu’il s’agisse d’ondes se propageant dans un milieu fluide indéfini ou d’ondes se propageant dans un tuyau indéformable ; il est par contre parfois difficile, dans le cas d’un liquide, de trouver une enveloppe assez rigide pour que ses déformations soient vraiment négligeables.
Il est bien évident que si l’enveloppe cède légèrement sous l’effet de la surpression du fluide, il en résulte une diminution de l’effort nécessaire pour allonger la colonne fluide d’une quantité donnée, ce qui revient à dire que tout se passe comme si le coefficient de compressibilité du fluide prenait une valeur plus grande : la célérité des ondes dans un fluide enfermé dans un tuyau s’abaisse lorsque les parois du tuyau deviennent moins résistantes.
4. Quelques exemples
4.1. Propagation d’ondes planes dans un liquide enfermé dans un tuyau
Nous choisissons comme premier exemple l’eau enfermée dans un tube indéformable. La célérité des ondes est :
\[\begin{aligned} &c=\frac{1}{\sqrt{\rho~\chi}}\\ &\rho=10^3~{\rm kg~m^{-3}}\quad;\quad\chi=5\times 10^{-10}~{\rm Pa}^{-1}\quad(c=1450~\rm m~s^{-1})\end{aligned}\]
La mesure de la célérité est faite de préférence en mesurant la vitesse de propagation des ondes planes dans une très grande étendue d’eau (un lac par exemple).
Au sein d’un tuyau, il est difficile d’éviter les déformations de l’enveloppe. Si, par exemple, l’eau est enfermée dans un tube d’acier de 10 cm de diamètre et de 1 mm d’épaisseur, la célérité n’est plus que de 1000 \(\rm m~s^{-1}\). Dans un tuyau en caoutchouc, elle tombe à quelques mètres par seconde seulement.
Résistivité acoustique : \[\mathcal{R}=\rho~c=1,45\times10^6~\rm kg~m^{-2}~s^{-1}\]
Soit par exemple un tube de 1 dm² de section attaqué par un piston en régime sinusoïdal à la fréquence 50 Hz et avec une amplitude de déplacement de 1 mm. L’amplitude de la vibration est : \[u_0=100~\pi\times10^{-3}=0,314~\rm m~s^{-1}\]
La puissance transmise par unité de surface (intensité de l’onde) est dans ces conditions : \[I=\frac{1}{2}~\rho~c~u_0^2=7\times10^4~\rm W~m^{-2}\]
Soit une puissance transmise par le tuyau : \[\overline{P}=I~S=700~\rm W\]
Les conditions que nous avons choisies correspondent à une amplitude de variation de la surpression au sein du tuyau : \[\delta p_0=\rho~c~u_0=1,45\times 10^6\times 0,314=5\times10^5~\rm Pa=5~atm.\]
Si la pression de repos \(P_0\) de l’eau au sein du tuyau n’est égale qu’à 1 atmosphère, l’eau passera par moment par des pressions négatives de – 4 atm et un phénomène de cavitation (décohésion de liquide avec apparition de bulles de vapeur) se produira.
Il conviendra donc, pour rendre possible la transmission d’une telle puissance par le tuyau, de maintenir sous une pression de repos supérieure à 5 atm. Même dans ces conditions, il est bien évident que la théorie élémentaire, qui se verra limitée à de faibles valeurs du rapport \(\delta p/P_0\), ne sera plus guère valable.
Il existe donc une limite supérieure à l’intensité que peut transporter sous forme d’onde progressive un liquide donné. La condition \(\delta p<P_0\) nous conduit à une intensité maximum : \[I_{max}=\frac{1}{2}~\rho~c~u_0^2=\frac{(\delta p_{max})^2}{2~\rho~c}=\frac{P_0^2}{2~\rho~c}\]
Pour \(P_0=1~\rm atm=10^5~Pa\), on trouve pour l’eau : \[I_{max}=\frac{10^{10}}{2}\times 1,45\times 10^6=5000~\rm W~m^{-2}\]
Pour \(P_0=50~\)atm, on trouverait 2500 fois plus, soit environ \(700~\rm W~cm^{-2}\).
En pratique, on pourra atteindre des intensités élevées en augmentant la pression de repos et en utilisant des liquides capables de supporter en régime discontinu des pressions négatives importantes sans se vaporiser (cf. le cours de thermodynamique).
4.2. Propagation d’ondes planes dans un barre rigide
Prenons le cas d’une barre d’acier pour laquelle le module d’élasticité et la masse spécifique sont respectivement : \[E=2\times10^{11}~\rm Pa\quad;\quad\rho=7800~kg~m^{-3}\]
D’où une célérité des ondes longitudinales et une résistivité acoustique : \[c=\sqrt{\frac{E}{\rho}}=5\times 10^3~\rm m~s^{-1}\quad;\quad\mathcal{R}=\rho~c=4\times 10^7~kg~m^{-2}~s^{-1}\]
Ces résultats sont en gros du même ordre de grandeur que pour les liquides.
4.3. Propagation d’ondes sonores dans un gaz (tuyau sonore)
Dans le cas des gaz, très compressibles, l’influence des déformations de l’enveloppe est beaucoup moins grande que pour les liquides. Pour calculer la valeur du coefficient de compressibilité, il nous faut définir les conditions dans lesquelles se produisent les compressions et les dilatations au sein du gaz. Les gaz étant mauvais conducteurs de la chaleur et les vibrations étant rapides, nous admettront que les compressions et les dilatations sont adiabatiques, ce qui est confirmé par les mesures de vitesse du son.
Assimilons le gaz à un gaz parfait. Son coefficient de compressibilité isotherme est \(1/P_0\) et son coefficient de compressibilité adiabatique \(1/\gamma~P_0\), \(\gamma\) étant le rapport des chaleurs spécifiques (7/5 pour un gaz diatomique comme l’air).
La célérité des ondes planes est donc : \[c=\sqrt{\frac{\gamma~P_0}{\rho}}=\sqrt{\gamma~r~T}=\sqrt{\frac{\gamma~R~T}{M}}\qquad\text{M : masse moléculaire}\]
La célérité est indépendante de la pression de repos, mais elle varie proportionnellement à la racine carrée de la température absolue (\(\gamma\) est à peu près constant dans un petit domaine de température. Cf. le cours de thermodynamique).
Avec les conditions suivantes : \[T=273~{\rm K}\quad;\quad\gamma=\frac{7}{5}\quad;\quad P_0=1,016\times 10^5~\rm Pa\quad;\quad\rho=1,293~kg~m^{-3}\]
on trouve : \(c~\cong~330~\rm m.s^{-1}\).
Dans les mêmes conditions, la résistivité acoustique est : \[\mathcal{R}=\rho~c=430~\rm kg~m^{-2}~s^{-1}\]
La célérité est du même ordre de grandeur que pour les liquides et les solides, car la faible valeur de la masse spécifique compense en partie la grande valeur de la compressibilité, mais la résistivité acoustique est beaucoup plus faible.
Il sera beaucoup plus difficile de faire passer de grandes intensités sonores dans un gaz en l’excitant par un piston mobile dont l’amplitude de déplacement est nécessairement limitée ; on obtiendra de grandes intensités sonores en excitant l’air par une masse gazeuse en mouvement (sirène).
4.4. Application à l’estimation de la sensibilité de l’oreille humaine
L’oreille est un récepteur de section 1 cm² environ, sensible – dans les meilleures conditions – à une surpression \(\delta p=10^{-4}\) Pa.
La puissance ainsi reçue est (en régime sinusoïdal) : \[\overline{P}=\frac{S(\delta p)^2}{2~\rho~c}=\frac{10^{-4}\times10^8}{860}=10^{-15}~\rm W\]
Il est curieux de constater que l’oreille est ainsi aussi sensible que l’œil qui peut voir une bougie à 20 km de distance, ce qui correspond à une puissance analogue tombant sur la pupille. On se rendra compte de l’ordre de grandeur de la puissance ainsi détectée en remarquant qu’une énergie de 1 joule pourrait alimenter cette puissance pendant \(0,98\times 10^{15}\) secondes, soit environ 100 millions d’années.
La fréquence étant de l’ordre de 1 kHz (sensibilité maximum de l’oreille) et l’amplitude de vitesse des couches d’air au voisinage du tympan étant : \[\frac{\delta p}{\mathcal{R}}=\frac{10^{-4}}{430}=2\times10^{-7}~\rm m~s^{-1}\]
L’amplitude de déplacement des tranches gazeuses est seulement : \[y_0=\frac{2\times 10^{-7}}{2000}\cong 3\times10^{-11}~\rm m=30~pm\quad\text{(picomètres)}\]
soit un déplacement des molécules inférieur à leur diamètre.
Il est bien entendu qu’il s’agit là d’un déplacement d’ensemble de toute la couche gazeuse ; les déplacements individuels des molécules – quoique beaucoup plus importantes et correspondant à des vitesses beaucoup plus élevées – n’ont aucune action sur le tympan du fait de leur incohérence. L’oreille n’est pas sensible aux déplacements désordonnés dus à l’agitation thermique des molécules gazeuses.
5. Vitesse du son aux fréquences élevées
Les méthodes modernes de mesure de la vitesse du son utilisent des ultra-sons de fréquence très élevée. On observe alors qu’aux très hautes fréquences (voisinage du mégahetz) le gaz semble se comporter – en ce qui concerne la célérité des ondes – comme un gaz monoatomique pour lequel \(\gamma=5/3\).
Cela tient à ce que la mise à l’équilibre thermique de l’énergie de rotation avec l’énergie cinétique de translation des molécules n’a plus le temps de se produire lorsque les variations de l’énergie cinétique de translation accompagnant les transformations adiabatiques du gaz sont très rapides.
L’énergie de rotation tend à garder une valeur constante, l’énergie de translation variant seule ; tout le travail de compression est dès lors utilisé à accroître la seule énergie de translation des molécules ; le gaz se comporte comme un gaz monoatomique pour lequel les rotations moléculaires ne sont pas modifiées par une élévation de température et n’interviennent pas dans le calcul de la chaleur spécifique.
Aux fréquences intermédiaires, on observe une variation progressive de la célérité qui passe, lorsque la fréquence s’accroît, de la valeur relativement faible qui correspond aux basses fréquences à une valeur plus élevée : il y a donc dispersion, c’est-à-dire variation de la célérité avec la fréquence, et cette dispersion est accompagnée d’une absorption qui peut devenir importante. Nous y reviendrons plus loin.
6. Vitesse du son et vitesse d’agitation thermique
Il est intéressant de comparer la vitesse du son dans un gaz donné, à une température donnée, à la vitesse moyenne d’agitation thermique des molécules du gaz à la même température. On ne comprendrait guère, en effet, comment la vitesse du son pourrait dépasser notablement la vitesse de translation des molécules elles-mêmes.
Or, la vitesse quadratique moyenne \(C\) des molécules est donnée par la relation : \[\frac{m~C^2}{2}=\frac{3}{2}~k~T\qquad\text{soit :}\quad C=\sqrt{\frac{3~R~T}{M}}\]
Elle est du même ordre de grandeur que la vitesse du son : \[c=\sqrt{\frac{\gamma~R~T}{M}}\]
Par contre, la vitesse du son dans les liquides (de l’ordre de 1500 m/s) est nettement supérieure à la vitesse moyenne d’agitation thermique aux températures usuelles. On interprète ce résultat en remarquant que le volume propre des molécules d’un liquide n’est plus, comme dans un gaz, négligeable devant le volume total.
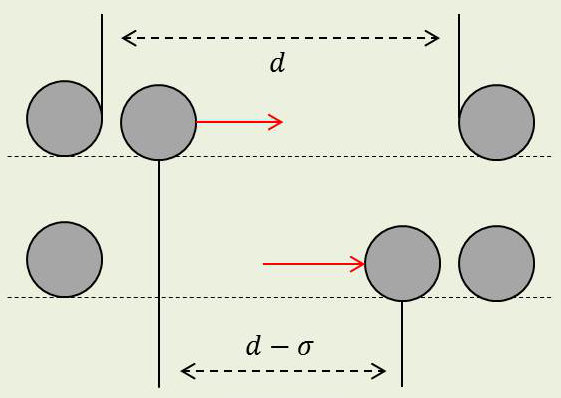 Une molécule recevant un choc sur sa gauche (cf. figure) vient frapper une molécule située sur sa droite, transmettant ainsi la vibration.
Une molécule recevant un choc sur sa gauche (cf. figure) vient frapper une molécule située sur sa droite, transmettant ainsi la vibration.
Le chemin parcouru par la molécule est plus court que le chemin parcouru par l’onde. Ce dernier est en effet égal à la distance \(d\) des centres des deux molécules alors que le chemin parcouru par la molécule elle-même est \(d-\sigma\) (\(\sigma\) étant le diamètre moléculaire).
On conçoit, grâce à ce raisonnement simplifié assimilant les molécules à des sphères rigides – comme on le fait dans l’établissement élémentaire de l’équation de Van der Waals – que la mesure du rapport des célérités dans un liquide et dans un gaz parfait à la même température permette d’obtenir des renseignements sur la valeur du volume libre au sein duquel se déplacent les molécules du liquide.

