1. Introduction

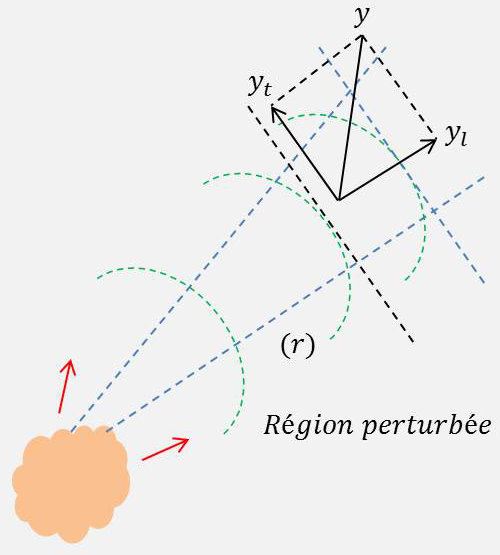Toute propagation variable au cours du temps imposée en une région quelconque d’un milieu solide indéfini se propage dans la masse du solide.

À grande distance de la région où est imposée la perturbation initiale (distance très supérieure au diamètre de la région perturbée), la propagation a lieu par ondes sphériques qui, dans un petit domaine (dimensions très petites devant la distance à la source de perturbation) sont assimilables à des ondes planes.

Nous nous proposons d’étudier la propagation de telles ondes planes de déformation.

Une déformation quelconque peut être représentée par la superposition de deux déformations :

• une déformation longitudinale (déplacements parallèles à la direction de propagation) ;

• une déformation transversale (déplacements perpendiculaires à la direction de propagation).

Nous étudierons successivement ces deux composantes.

2. Ondes longitudinales

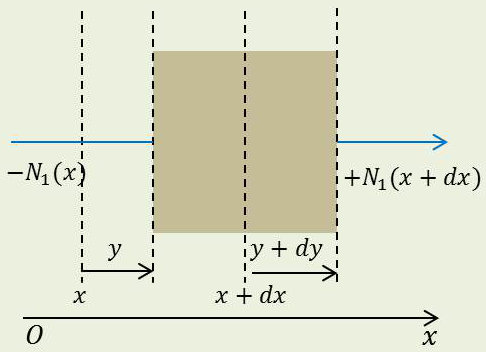Une section unité du plan d’abscisse \(x\) au repos a subi à l’instant \(t\) un déplacement, dans la direction \(Ox\) normale au plan, égal à \(y(x,~t)\). Tous les points du plan (dans la région étudiée) ont subi le même déplacement (plan d’onde).

Une tranche de solide de hauteur \(dx\) est soumise à des efforts normaux de traction sur ses bases : \[[x,~x+dx]\quad\Rightarrow\quad[-N_1(x),~N_1(x+dx)]\]

Il en résulte un allongement relatif : \[\frac{\delta(dx)}{dx}=\frac{\partial y}{\partial x}=a_1\]

avec : \[N_1=\lambda~\theta+2~\mu~a_1\quad;\quad\theta=a_1\]

puisque les contractions latérales sont interdites.

En définitive, on a : \[N_1=(\lambda+2~\mu)~\frac{\partial y}{\partial x}\]

La tranche de solide de base unité et de hauteur \(dx\) donc de masse \(\rho.dx\) (en introduisant la messe spécifique) est accélérée vers les \(x>0\) par la force \[dN_1=\frac{\partial N_1}{\partial x}~dx\]

D’où l’équation : \[\rho~\frac{\partial^2y}{\partial t^2}=(\lambda+2~\mu)~\frac{\partial^2y}{\partial x^2}\]

Il vient : \[\frac{\partial^2y}{\partial t^2}=c^2~\frac{\partial^2y}{\partial x^2}\quad;\quad c=\sqrt{\frac{\lambda+2~\mu}{\rho}}\]

C’est la vitesse de propagation des ondes longitudinales.

Comme \(\lambda+2~\mu>E\) (interdiction des contractions latérales entraînant un effort plus grand pour un allongement donné), cette vitesse de propagation est supérieures à celle des ondes planes longitudinales dans une barre constituée par le même matériau.

3. Ondes transversales. Propagation

Les déplacements sont maintenant situés dans le plan d’onde. Tous les points d’une surface unité du plan d’abscisse \(x\) au repos ont subi, à l’instant \(t\), le même déplacement \(y(x,t)\) normal à la direction de propagation \(Ox\).

Les fibres du solide qui se trouvaient, au repos, parallèles à \(Ox\) sont, à l’instant \(t\), inclinées sur \(Ox\) d’un angle \[\alpha(x,~t)=\frac{\partial y}{\partial x}\]

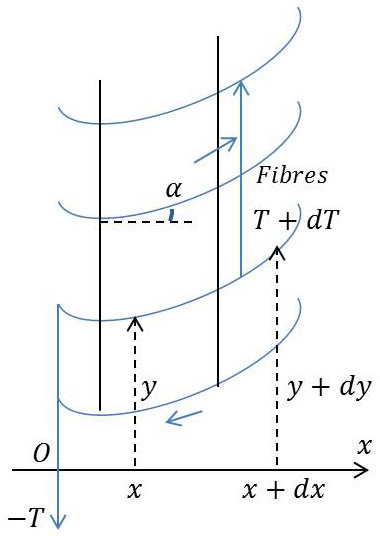Les plans perpendiculaires à \(Ox\) au repos gardent une direction fixe, un parallélépipède de base unité et de hauteur \(dx\), rectangle au repos, voit ses génératrices s’incliner, par rapport à sa base de cet angle.

Ce qui nécessite un effort uniformément réparti sur sa base \(x\) : \[T(x,~t)=\mu~\frac{\partial y}{\partial x}\]

Sur la base \(x+dx\), l’effort tranchant est \(T(x+dx,~t)\).

La différence de ces deux efforts donne au parallélépipède une accélération verticale, telle que : \[\rho~dx~\frac{\partial^2y}{\partial t^2}=dT=\frac{\partial T}{\partial x}~dx=\mu~\frac{\partial^2y}{\partial x^2}\]

On obtient ainsi l’équation de propagation des vibrations transversales : \[\frac{\partial^2y}{\partial t^2}=c'~\frac{\partial^2y}{\partial x^2}\quad;\quad c'=\sqrt{\frac{\mu}{\rho}}\]

C’est la vitesse de propagation des ondes transversales.

4. Remarques

1) La vitesse de propagation des ondes transversales est nettement supérieure à la vitesse de propagation des ondes longitudinales dans une barre du même matériau (\(\mu\cong 0.4E\)) et a fortiori à la vitesse de propagation des ondes longitudinales dans le milieu solide indéfini.

2) Dans un liquide (\(\mu=0\)) la vitesse de propagation de ces ondes est nulle : un liquide (ou un gaz) ne peut propager d’ondes transversales.

3) La rotation du parallélépipède considéré plus haut est empêchée par l’apparition d’efforts tranchants sur les génératrices supérieures et inférieures ; ces efforts compensent le couple \(T~dx\) et ont une résultante nulle suivant \(Ox\), l’ensemble de ces efforts restant invariable par translation suivant \(Ox\).

Nous allons maintenant étudier les vibrations transversales d’un barreau (verge vibrante) de section limitée, où des efforts tranchants latéraux vont nécessairement disparaître.

Il en résulte une rotation des sections droites et des déformations de glissement très faibles qui sont même rigoureusement nulles au voisinage de la surface latérale (voir plus haut), les déformations principales étant des allongements ou raccourcissements de fibres.

Nous obtiendrons une loi de propagation très différente pour les déformations transversales.