1. Question de principe

La célérité de la lumière dépend-elle de la vitesse de la source émettrice, mesurée par rapport à l’espace absolu ? Les physiciens, installés dans leur vaisseau spatial, mesurant la vitesse de la lumière arrivant au devant d’eux, ou derrière eux, devraient trouver les valeurs \(c \pm v\) ce qui mettrait en évidence le mouvement absolu de leur vaisseau.

Est-il besoin d’imaginer un laboratoire spatial pour réaliser cette expérience ? La Terre suffit puisqu’elle se déplace à la vitesse prodigieuse de 30 km/s sur son orbite. On peut d’ailleurs admettre pendant la durée d’une expérience qu’elle effectue un mouvement de translation uniforme. C’est cet effet qui a été exploité par l’américain Michelson.

2. Les étoiles doubles

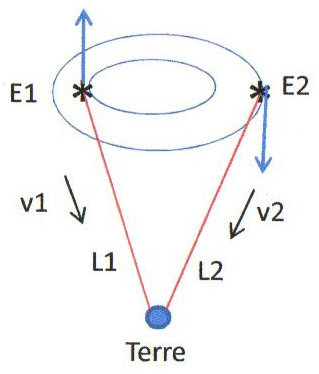Pour les relativistes, quelle que soit la vitesse de la source émettrice, la célérité de la lumière est constante. Les étoiles doubles sont une preuve expérimentale de cette affirmation. Une étoile double est un système de deux étoiles très proches (mais discernables avec une lunette très puissante) tournant l’une autour de l’autre suivant les lois de la gravitation universelle. Leurs distances respectives à la Terre sont pratiquement égales mais l’une peut parfois se déplacer en direction de la Terre, l’autre se déplaçant en sens inverse.

La lumière parvient cependant au même moment sur la Terre (même retard). Les astronomes ont vérifié la cohérence des résultats de leurs observations sur le mouvement des étoiles. On peut donc confirmer que \(v_1 = v_2\) ce qui signifie que la vitesse de la lumière est constante et ne dépend pas du mouvement de la source.

3. Expérience de Michelson

L’expérience de Michelson se compose de :

• \(M_1\) et \(M_2\) : deux miroirs plans ;

• \(M\) : une glace sans tain ;

• \(S\) : une source de lumière ;

• \(L\) : une lunette (observateur).

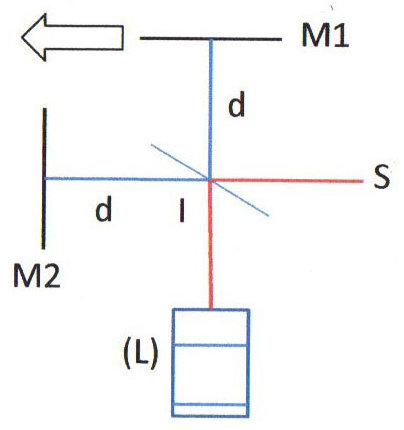Les deux trajets lumineux \(SIM_1IL\) et \(SIM_2IL\) viennent se combiner en \(L\).

Les trajets lumineux sont géométriquement identiques. Cependant, si l’on incline très légèrement le miroir \(M_2\), il apparaît une petite différence de marche et l’on peut observer des franges de coin d’air. Le trajet perpendiculaire au sens du déplacement du système est dit transversal. L’autre trajet parallèle au sens du déplacement du système est dit longitudinal. Tel est le principe simplifié de l’interféromètre de Michelson. L’ensemble se déplace à la vitesse \(v\), vitesse de la Terre sur son orbite.

Nous allons comparer les temps de trajet. Cette différence devrait engendrer à priori une différence de marche, donc une modification des franges d’interférences du coin d’air.

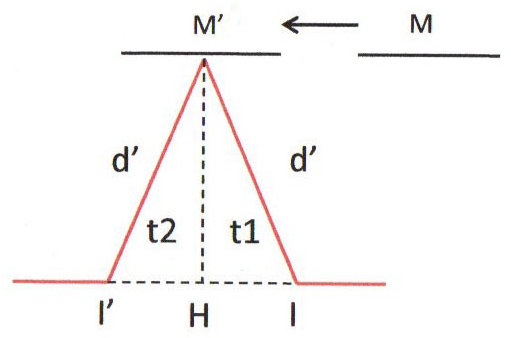Trajet longitudinal

\[\begin{aligned} t_1 &= t_{IM_2I} \\ t_1 &= \frac{d}{c-v}+\frac{d}{c+v} \\ t_1 &= \frac{2~d~c}{c^2-v^2}=\frac{2~d/c}{1-v^2/c^2}\end{aligned}\]

On sait par ailleurs que \( \beta= v / c \) avec \(v\ll c\).

Il vient donc : \[t_1 \approx \frac{2~d}{c}~(1 + \beta^2)\]

Trajet transversal \[t_2 = t_{IM_1I} = \frac{2~d'}{c}\] \[d'=\sqrt{d^2-(v~t_2)^2} = \sqrt{d^2~(1+v^2~\Big(\frac{t_2}{d}\Big)^2}\]

Par suite : \[d' = d \; (1+\beta^2)\] \[t_{IM_2I} = 2~\frac{d'}{c} = 2~\frac{d}{c}~\Big(1+\frac{\beta^2}{c}\Big)\]

D’où un écart temporel : \[\Delta t=\frac{2~d}{c}~(1+\beta^2)-\frac{2~d}{c}~\Big(1+\frac{\beta^2}{2}\Big)=\frac{d}{c}~\beta^2\]

Donc une différence de marche : \[\Delta d = c~\Delta t = d~\beta^2\]

Michelson était sûr de déceler un écart de 1/20 de frange avec son appareil. Il devait en principe déceler cette différence de marche. Il y avait une distance \(d\) = 20 m et un rapport (vitesse de la Terre / vitesse de la lumière) de l’ordre de \(10^{-4}\).

Michelson devait s’attendre à obtenir \( \Delta d = c\) et \(\Delta t = 0,2~\)µm, c’est-à-dire un décalage d’une demi-frange. Il n’en a cependant observé aucune. On ne pouvait qu’en conclure que la vitesse de la lumière était constante.

Lorentz avait émis l’hypothèse d’une compression de l’éther, cet étrange fluide hypothétique grâce auquel on expliquait, aux XVII° et XVIII° siècles la propagation de la lumière. Mais, avec cette hypothèse, il aurait fallu admettre alors que tous les corps fussent contractés.