1. Température et entropie

Dans l’étude du comportement d’un système, la thermodynamique se distingue de la mécanique par l’introduction du concept de température T.

Considérant une assemblée très nombreuse d’éléments individuels tels que molécules, atomes, particules élémentaires, etc., il n’est pas nécessaire de s’intéresser au comportement individuel de ces éléments.

Ainsi apparaît la notion de température T, intimement liée à celle d’équilibre statistique. À ce concept est associée la notion d’entropie S qui caractérise l’état de désordre d’un système.

Principe fondamental : l’entropie S ne peut pas diminuer au cours d’une transformation d’un système qui n’échange pas de travail avec l’extérieur.

2. Macroscopique et microscopique

Le problème peut être abordé de deux manières profondément différentes : on peut ignorer le comportement détaillé des divers éléments du système, autrement dit son aspect microscopique ou bien prendre en considération des propriétés d’ensemble pour s’intéresser à son aspect macroscopique. Une démarche présentant une certaine analogie avec la façon d’aborder le problème économique : micro-économie et macro-économie.

Ces propriétés nouvelles de température et d’entropie peuvent être introduites comme conséquences d’un certain nombre de principes généraux qui constituent la base de ce que l’on appelle la thermodynamique classique.

On peut, au contraire, considérer le comportement détaillé des divers éléments du système. Dans ce cas, la complexité du problème rend indispensable le recours aux méthodes de la mécanique statistique. À partir d’une seule hypothèse donnée (Boltzman, Fermi-Dirac, Bose-Eisntein, etc.), on peut introduire de façon logique, les deux notions fondamentales de température et d’entropie. Tels sont les fondements et le principe de la thermodynamique statistique.

3. Descriptions du système

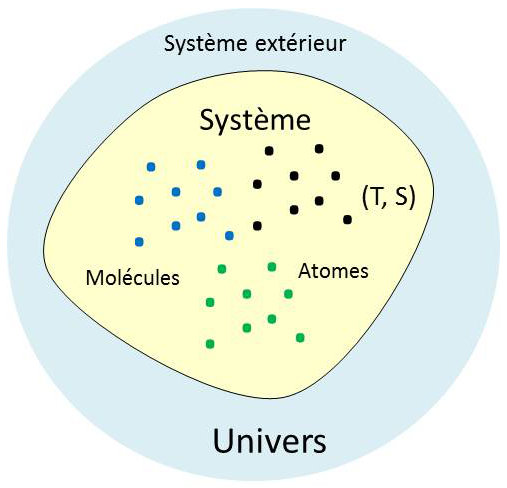
Nous désignons sous le nom de système une portion de l’espace (ou de matière) isolée - par la pensée - du reste de l’Univers, devenu alors milieu extérieur.

Le système peut être alors étudié en choisissant des quantités permettant de décrire :

• d’une part le comportement du système,

• d’autre ses interactions avec le milieu extérieur.

3.1. Description macroscopique

La description macroscopique d’un mélange, gazeux par exemple, ne nécessite que la détermination de sa composition chimique, de sa masse, de son volume, de sa pression, enfin de sa température.

Il s’agit d’un petit nombre de variables (appelées parfois coordonnées), suffisantes, aisément mesurables et accessibles à nos sens. Elles n’impliquent aucune hypothèse sur la structure intime de la matière.

3.2. Description microscopique

Supposons qu’il s’agisse d’un gaz, formé d’un très grand nombre de molécules, disposées au hasard dans une enceinte et animées de vitesses a priori quelconques. Une molécule déterminée pourra être décrite par un total de 6 coordonnées :

• trois paramètres de position (\(x,~y,~z\)) ;

• trois paramètres de vitesse (\(v_x,~v_y,~v_z\)).

Le point représentatif dans un espace à 6 dimensions est dénommé extension en phase. Cette extension est partagée en petites cellules de volume \(d\tau\). À l’intérieur de chacune d’elles, les 6 coordonnées varient peu autour d’une valeur moyenne.

En numérotant ces cellules, on peut obtenir une description microscopique du gaz en déterminant le nombre de molécules dont le point représentatif se trouve dans une i-ième cellule.

Une telle description est utilisée en mécanique statistique. Elle exige une hypothèse sur la matière et fait intervenir des coordonnées très nombreuses, inaccessibles à nos sens et surtout non directement mesurables.

3.3. Macroscopique ou microscopique

Une cohérence est nécessaire. Les deux descriptions doivent se trouver en accord lorsqu’il s’agit de prévoir des phénomènes mesurables. Par exemple, la pression peut apparaître comme la moyenne des impulsions élémentaires communiquées à la paroi par les chocs des molécules individuelles.

La description macroscopique présente l’avantage d’être indépendante de toute hypothèse, susceptible de modification par suite de l’évolution des connaissances. Elle peut être néanmoins sujette à caution, en présentant souvent l’avantage de permettre une interprétation plus claire des phénomènes.

Dans une description macroscopique, donc dans un cadre de thermodynamique classique, nous dirons qu’un système est dans un état bien déterminé lorsque l’ensemble de ses propriétés physiques est parfaitement déterminé. Ceci implique que la connaissance de l’état dans lequel se trouve le système permet de prévoir le comportement du système vis-à-vis de toute action extérieure, donc de toute modification du milieu extérieur.

Nous désignons sous le nom de variables (ou coordonnées) thermodynamiques, les quantités macroscopiques qui permettent de décrire l’état interne d’un système. Le but de la thermodynamique est de déduire d’un certain nombre de principes fondamentaux des relations entre ces coordonnées.