1. Généralités
On considère un système thermodynamique quelconque qui subit une déformation, ou un déplacement, sous l’action d’une force extérieure. Cette force exerce sur le système un travail égal au produit de la force par la composante du déplacement dans sa direction.
D’une façon très générale, nous considérons que le système échange du travail avec le milieu extérieur lorsque l’évolution qu’il subit peut être imaginée comme accompagnant une modification purement mécanique du milieu extérieur telle que l’élévation ou l’abaissement d’un poids dans le champ de pesanteur.
Dans ces échanges de travail, nous conviendrons de compter positivement le travail lorsqu’il est reçu par le système (c’est-à-dire lorsque l’on peut imaginer la modification du système comme accompagnant l’abaissement d’un poids dans le milieu extérieur) ; nous compterons négativement le travail lorsqu’il est fourni par le système au milieu extérieur.
 Par exemple, le système peut être constitué par une masse gazeuse enfermée dans un corps de pompe où un piston chargé par une masse m peut coulisser sans frottement. Le tout est placé dans le vide.
Par exemple, le système peut être constitué par une masse gazeuse enfermée dans un corps de pompe où un piston chargé par une masse m peut coulisser sans frottement. Le tout est placé dans le vide.
Si la masse est assez importante, le piston s’enfonce, la masse gazeuse reçoit un travail qui résulte de l’abaissement dans le champ de pesanteur de l’ensemble masse - piston.
Si elle est faible, le piston monte, le système fournit le travail au milieu extérieur : il en reçoit donc un travail négatif.
Dans tous les cas, le travail reçu par le système dans une transformation donnée peut être calculé à partir des modifications du milieu extérieur qui lui sont liées ou que nous pouvons imaginer lui être liées.
Nous allons chercher maintenant à quelles conditions le travail reçu par le système pourra être déterminé à partir des données macroscopiques relatives au système lui-même.
2. Transformations quasi statiques
2.1. Définitions
Lorsqu’il reçoit du travail (positif ou négatif), le système évolue. Pour que cette évolution puisse être exprimée par la variation de coordonnées thermodynamiques, il faut que, tout au long de l’évolution, de telles coordonnées puissent être assignées au système pour représenter son état. Il faut pour cela que l’état du système soit à chaque instant infiniment voisin d’un état d’équilibre thermodynamique.
Convenons de désigner cet état d’équilibre thermodynamique, infiniment voisin de l’état du système, sous le nom d’état d’équilibre tangent et supposons qu’à tout instant de l’évolution toutes les variables thermodynamiques et toutes les forces agissant sur le système ont des valeurs infiniment voisines de celles qui existeraient dans un état d’équilibre tangent.
La transformation subie par le système sera alors désignée sous le nom de transformation quasi statique.
2.2. Exemple
Nous reprenons le corps de pompe précédent en supposant que l’ensemble est maintenu en équilibre thermique (température T) avec le milieu extérieur grâce à une cloison diatherme. On désigne par \(m\) la masse du piston et par \(M\) la masse posée sur le piston. Si l’on place une surcharge \(M'\) sur ce piston, celui-ci va descendre d’une hauteur \(z\) à laquelle il se fixera après quelques oscillations.
Le travail reçu par le gaz pendant cette transformation sera : \[W~=~(M+M'+m)~g~dz\]
Nous exprimons ainsi le travail reçu par le système au moyen de données relatives au milieu extérieur, ce qui est toujours possible. Mais nous ne saurions exprimer \(W\) à partir de coordonnées thermodynamiques relatives au gaz lui-même, ces coordonnées n’étant pas définies en cours d’évolution.
Supposons par contre que nous ayons ajouté sur le piston une surcharge infiniment petite ; celui-ci s’abaisse d’une quantité infiniment petite \(dz\), la pression \(p\) augmente d’une quantité infiniment petite, l’équilibre thermique est très peu perturbé et la température se maintient à \(T \).
Le travail reçu par le gaz dans cette transformation infiniment petite et quasi statique est : \[(M+m)~g~dz=p~S~dz=-p~dv\]
-
\(S\) : section du corps de pompe
-
\(dv\) : variation (algébrique) de volume du gaz
Dans cette transformation, nous observons donc que le travail infinitésimal reçu par le gaz s’exprime en fonction des seules coordonnées thermodynamiques \(p\) et \(v\) du système.
Poursuivons l’expérience toujours dans les mêmes conditions, c’est-à-dire en ajoutant des surcharges infiniment petites.
La pression du gaz équilibre continuellement la force extérieure et varie d’une façon déterminée en fonction du volume v occupé par le gaz. Le travail total reçu par le gaz dans une transformation quasi statique finie pourra s’écrire : \[W~=~\oint -p~dv\]
L’intégrale est prise le long de la courbe représentant \(p\) en fonction de \(v\) pendant la transformation.
Cette courbe est isotherme dans le cas particulier que nous avons choisi ; mais on peut très bien imaginer une transformation quasi statique quelconque le long de laquelle \(p\) est lié à \(v\) par une relation déterminée.
On aboutit au même type d’intégrale, celle-ci étant prise le long de la courbe représentant \(p=f(v)\).
Le point important est que, dans la transformation quasi statique élémentaire où \(v\) varie de \(dv\), le travail infinitésimal reçu par les forces de pression extérieures peut être exprimé à partir des seules variables macroscopiques définissant l’état du système gazeux.
2.3. Conclusions
Le travail reçu par le système dans une transformation quelconque, quasi statique ou non, peut toujours être calculé à partir des données relatives au milieu extérieur qui fournit ce travail.
Le travail reçu par un système dans une transformation quasi statique élémentaire peut toujours être calculé à partir des données thermodynamiques du système (certaines d’entre elles apparaissant sous forme différentielle).
3. Transformations réversibles
Considérons le système précédent supposé idéal (sans frottement solide). Si on enlève une à une les surcharges infinitésimales, le piston s’élève et le travail fournit au milieu extérieur un travail positif \([p~dv]\). Nous voyons ainsi le gaz repasser par les états qu’il avait occupés successivement lors de la compression quasi statique isotherme considérée plus haut.
Pour ce système idéal, nous pouvons envisager que les surcharges nécessaires pour entraîner le mouvement du piston sont nulles et que la compression isotherme quasi statique peut être suivie d’une détente isotherme quasi statique où le gaz repasse exactement par les mêmes états en sens inverse.
Une telle transformation idéale qui consiste dans le passage à travers une suite d’états d’équilibre, dans un sens ou dans l’autre, sera désignée sous le nom de transformation réversible. Par contre, les expériences fondées sur des phénomènes dissipatifs sont essentiellement irréversibles, même si elles sont conduites de façon infiniment lentes.
Une transformation ne peut être réversible que si elle est quasi statique, mais une transformation quasi statique n’est pas toujours réversible ; par exemple, l’allongement d’un fil métallique par traction dans le domaine inélastique est une transformation irréversible, même si elle est conduite de façon quasi statique.
En résumé, pour qu’une transformation soit réversible, il faut :
-
qu’elle soit quasi statique, ce qui élimine notamment l’intervention des phénomènes dissipatifs qui s’annulent avec la vitesse de transformation (par exemple, frottement visqueux ou effet Joule) ;
-
qu’aucun phénomène dissipatif du type qui ne s’annule pas avec la vitesse (par exemple frottements solides, inélasticité, hystérésis, etc.) n’intervienne au cours de la transformation.
Comme il est impossible de supprimer totalement tous les phénomènes dissipatifs (notamment les frottements) dans une expérience réelle, nous voyons déjà qu’une transformation réversible est irréalisable en toute rigueur et ne peut être qu’indéfiniment approchée.
Nous la considérons comme possible à la limite lorsque tous les phénomènes dissipatifs sont éliminés dans un appareil idéal.
3.1. Exemples de transformations réversibles élémentaires
Considérons le travail des forces de pression dans une déformation, par exemple le cas du gaz enfermé dans le corps de pompe. Nous allons montrer que, quelque soit la forme de l’enceinte enfermant le gaz, une variation de volume \(dv\) de cette enceinte conduite de manière réversible entraîne la réception par le gaz d’un travail \([-p~dv\)].
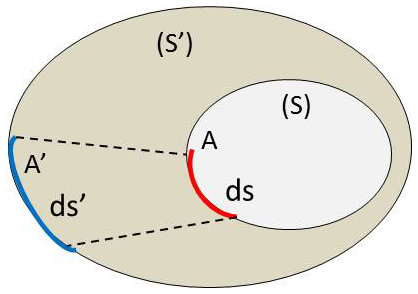 Ex. 1 : Soit \((S)\) la surface limitant la masse gazeuse de volume \(v\). Le gaz se trouve à l’équilibre thermodynamique à la pression uniforme \(p\).
Ex. 1 : Soit \((S)\) la surface limitant la masse gazeuse de volume \(v\). Le gaz se trouve à l’équilibre thermodynamique à la pression uniforme \(p\).
Supposons que \((S)\) se déforme d’une quantité infinitésimale et passe à \((S')\), le volume du gaz passant de \(v\) à \(v+dv\). La pression reste constante à un infiniment petit près.
Lors de la déformation, un point de la surface \((S)\) tel que \(A\) passe en un point \(A'\) de la surface \(S'\). Un élément \(dS\) entourant \(A\) passe en \(dS'\) entourant \(A'\).
La force de pression exercée par le gaz sur \(dS\) est dirigée suivant la normale à \(dS\), vers l’extérieur de l’enceinte, et égale à \(p~dS\). Son travail élémentaire (ou travail reçu par le gaz) est : \[dW=p~\overrightarrow{dS}\cdot\overrightarrow{AA'}=-p~dv\]
Ex. 2 : La f.é.m. d’une pile impolarisable étant \(E\), le passage d’une charge \(dq\) de façon réversible du pôle \(+\) au pôle \(–\) à l’intérieur de la pile correspond à la réception par la pile du travail élémentaire : \[dW~=~E~dq\]
Ex. 3 : Soit \(F\) la tension mécanique d’un fil et \(l\) sa longueur. Au cours d’un allongement quasi statique, le fil reçoit le travail élémentaire : \[dW~=~F~dl\]
Si la force \(F\) est assez faible pour que les déformations soient parfaitement élastiques, la transformation est réversible. Si la limite élastique du fil est dépassée, l’allongement \(dl\) est irréversible.
S’il a été obtenu par exemple par un accroissement \(dF\) de la force de tension, une diminution ultérieure de cette force de \(dF\) ramènera bien la tension à sa valeur initiale, mais elle ne ramènera pas à sa valeur initiale la longueur du fil qui conservera un résidu d’allongement. Le travail reçu par le fil dans l’allongement \(dl\) est cependant toujours fourni par la relation précédente, valable à la seule condition que l’allongement soit quasi statique.
4. Variables intensives et variables extensives
Considérons un système \(S\) à l’équilibre thermique formé de deux parties \(A\) et \(B\) en équilibre. Nous pouvons définir l’état du système \(S\) par un ensemble de coordonnées thermodynamiques et définir séparément l’état de chacune des parties \(A\) et \(B\) par les deux ensembles de valeurs que prennent respectivement, pour \(A\) et \(B\), les mêmes variables thermodynamiques.
Nous observons alors que :
-
certaines variables ont la même valeur pour chacune des parties \(A\) et \(B\) à l’équilibre et pour l’ensemble du système \(S\), ces variables seront désignées sous le nom de variables de tension ou variables intensives ;
-
certaines variables ont pour le système global \(S\) une valeur égale à la somme des valeurs qu’elles présentent dans les parties \(A\) et \(B\), ces variables seront désignées sous le nom de variables de quantité ou variables extensives.
En nous référant aux exemples précédents :
-
Variables intensives : pression, f.é.m., tension mécanique, température ;
-
Variables extensives : volume, charge, longueur de fil.
Nous remarquons en outre que, dans chaque cas, le travail reçu par le système dans une transformation réversible élémentaire pouvait être exprimé sous la forme du produit d’une variable de tension par la variation infiniment petite d’une variable de quantité.
D’une façon générale, le travail reçu par un système quelconque dans une transformation réversible élémentaire pourra être mis sous la forme : \[dW=X~dx+Y~dy+Z~dz\]
-
\(X,~Y,~Z\) sont des variables intensives ;
-
\(x,~y,~z\) sont des variables extensives associées respectivement à \(X,~Y,~Z\).
Dans les exemples précédents, nous avions les associations : \([E,~q]\) ; \([F,~l]\) ; \([-p,~v]\).
5. Travail reçu dans une transformation réversible finie
Pour fixer les idées, revenons au cas d’un gaz soumis à des forces de pression. Faisons varier de façon réversible le volume de ce gaz du volume initial \(V_i\) au volume final \(V_f\).
On sait que le travail total reçu par le gaz est donné par l’intégrale : \[W=\oint-p~dv\]
Le symbole employé pour l’intégration indique qu’il s’agit d’une intégrale curviligne se rapportant à une succession d’états d’équilibre bien déterminés. En d’autres termes, pour pouvoir calculer le travail, il nous faut connaître, non seulement l’état initial et l’état final du système, mais aussi tous les états intermédiaires.
La pression \(p\) est fonction du volume \(v\) et de la température \(T\), d’après l’équation d’état. Pour pouvoir effectuer l’opération, il faut que \(p\) soit une fonction connue de \(v\) et de \(v\) seulement, tout au long de la transformation. Il suffira par exemple que nous connaissions la température \(T\) qui correspond à chacune de valeurs successives de \(V\).
D’où le résultat très important :
Le travail reçu par un système dans une transformation réversible finie dépend, en général, non seulement de l’état initial et de l’état final du système, mais encore de tous ses états intermédiaires.
6. Représentation graphique du travail
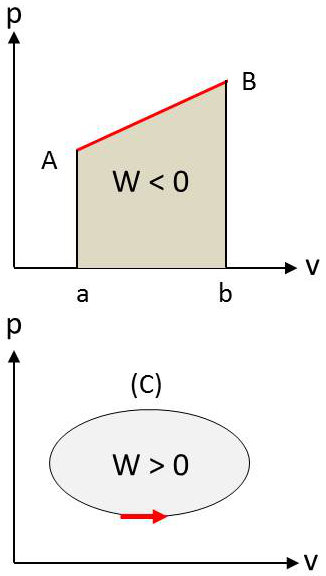 Considérons l’exemple de la masse gazeuse et représentons ses états successifs par une succession de points dans le diagramme \((p, v)\), dit diagramme de Clapeyron.
Considérons l’exemple de la masse gazeuse et représentons ses états successifs par une succession de points dans le diagramme \((p, v)\), dit diagramme de Clapeyron.
Remarquons qu’à chaque état d’équilibre représenté par le point \((p, v)\) correspond, d’après l’équation d’état, une température \(T\) bien déterminée, ce qui définit complètement l’état de la masse gazeuse.
La succession des états d’équilibre occupés par le gaz au cours de la transformation est représentée par une courbe \((C)\) dans le diagramme \((p, v)\).
On voit immédiatement que le travail \([-p~dv]\) dans la transformation est mesurée par l’aire \([aAbB]\) en couleur comptée positivement dans toutes les portions où le sens de la transformation correspond à une diminution de \(V\).
Le travail reçu par le gaz dans un cycle réversible est numériquement égal à l’aire colorée dans la représentation graphique du cycle. Il est positif si le cycle est parcouru dans le sens direct (sens trigonométrique).
Si le cycle comprend plusieurs boucles, il faudra évidemment additionner algébriquement leurs aires.
6.1. Compression et détente isotherme d’un gaz parfait
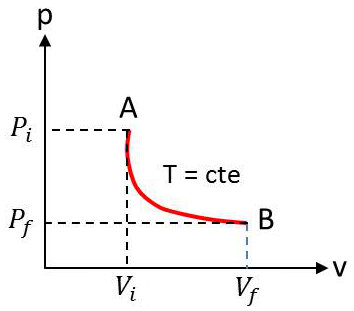 À titre d’exemple, nous allons calculer le travail reçu par le système constitué par \(n\) moles de gaz parfait passant de l’état d’équilibre \([p_i,~v_i,~T]\) à l’état d’équilibre \([p_f,~v_f,~T]\) en restant constamment à la même température \(T\).
À titre d’exemple, nous allons calculer le travail reçu par le système constitué par \(n\) moles de gaz parfait passant de l’état d’équilibre \([p_i,~v_i,~T]\) à l’état d’équilibre \([p_f,~v_f,~T]\) en restant constamment à la même température \(T\).
Nous spécifions le chemin suivi puisque nous lui imposons d’être isotherme. Nous supposons la transformation réversible.
La variable \(p\) est parfaitement définie pour chaque valeur de \(v\) et le travail est calculable. \[W=\int_{V_i}^{V_f} -p~dv=\int_{V_i}^{V_f}-\frac{n~R~T}{v}~dv\]
On a donc : \[W=n~R~T~\log\frac{V_i}{V_f}=n~R~T~\log\frac{P_i}{P_f}\quad;\quad\text{T=cte}\]
Le chemin suivi dans le diagramme \([p,~v]\) est donc une portion d’hyperbole équilatère.
Par exemple : 1 mole de gaz parfait qui se détend réversiblement à la température de la glace fondante de 10 atmosphères à 1 atmosphère reçoit le travail : \[W=-R~T_0~\log(10)=-8,32\times 273\times 2,3=-5200~\text{joules}\]
Elle fournit donc 5,2 kJ au milieu extérieur.

