1. Écarts à la loi de Mariotte

L’expérience montre qu’aucun gaz réel ne suit, en toute rigueur et aux pressions usuelles, les lois de Mariotte et de Joule.

Pour une température déterminée, le produit \(p~v\) n’est pas absolument indépendant de la pression \(p\). Ce fait peut être mis en évidence en représentant l’état du gaz par de nouvelles variables \(p~v\) et \(p\). Il s’agit du diagramme d’Amagat.

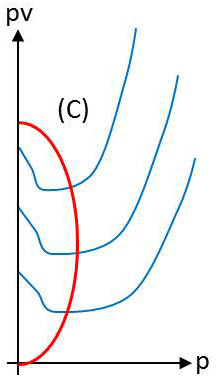On porte en abscisse la pression \(p\) et en ordonnée le produit \(p~v\). Dans cette représentation, les isothermes \((T = cte)\) seraient des droites horizontales pour un gaz parfait.

Sur la figure ci-contre, on a représenté quelques isothermes à température assez élevée pour qu’aucun phénomène de condensation (passage du gaz à l’état liquide) ne se produise.

Nous observons qu’à température élevée les isothermes ont partout une pente positive et que, par contre, ils présentent un minimum pour des températures plus basses. Ces minimums sont répartis sur une courbe à allure parabolique.

D’une façon générale, la pente \(m\) d’un isotherme en un point donné peut être mis sous la forme :

\[\begin{aligned} &m~=~\Big(\frac{\partial(p~v)}{\partial p}\Big)_T~=~v+p~\Big(\frac{\partial v}{\partial p}\Big)_T\\ &m~=~p~v~\Big\{\frac{1}{v}~\Big(\frac{\partial v}{\partial p}\Big)_T+p\Big\}\end{aligned}\]

C’est-à-dire encore : \[m=(\chi_0-\chi)~p~v\]

\(\chi\) : coefficient de compressibilité isotherme: \[\chi=-\frac{1}{v}~\Big(\frac{\partial v}{\partial p}\Big)_T\]

\(\chi_0\) : coefficient de compressibilité isotherme du gaz parfait à la même pression : \[\chi_0~=~\frac{1}{p}\]

Si la pente \(m\) est négative (points représentatifs à l’intérieur de la courbe C), alors \(\chi>\chi_0\) et le gaz est plus compressible que le gaz parfait. C’est le cas de la majorité des gaz réels dans les conditions ordinaires de température et de pression.

Si au contraire \(m\) est positive (points représentatifs à l’extérieur de la courbe C) la gaz est moins compressible que le gaz parfait. C’est le cas de l’hydrogène dans les conditions usuelles de température et de pression.

Sur la courbe C, le gaz suit localement la loi de Mariotte, mais il ne faudrait pas en conclure qu’il se rapproche de l’état parfait : le produit \(p~v\) est notamment différent en ces points, tout au moins en général, de la valeur \(n~R~T\) (n nombre de moles) qu’il prend pour un gaz parfait.

La quantité \(n~R~T\) est représentée sur le diagramme par l’ordonnée à l’origine (sur l’axe des \(p~v\)) de l’isotherme \(T\).

En effet, la loi d’Avogadro s’applique aux gaz réels pris à une pression suffisamment faible. Les n moles du gaz considéré, prises à une pression \(p=\varepsilon\) (très faible), occupent donc le même volume que \(v\) (très grand) à la température \(T\) que n moles de gaz parfait dans les mêmes conditions de température et de pression.

On a donc si \(p\) est très faible (\(p=\varepsilon\)) : \[(p~v)_{g.r.}~=~(p~v)_{g.p.}~+~n~R~T \qquad\text{g.r. pour gaz réel, g.p. pour gaz parfait}\]

Soit, pour le gaz réel, une ordonnée à l’origine de l’isotherme d’Amagat correspondant à la température \(T\) : \[lim_{p\rightarrow 0}(p~v)=n~R~T\]

2. Représentation de Clapeyron

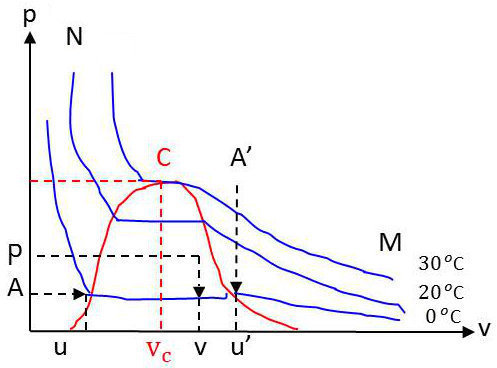On peut aussi représenter les états du gaz dans le diagramme \([p,v]\) de Clapeyron et tracer les isothermes qui correspondent à une série de températures croissantes.

La représentation ci-contre correspond aux résultats obtenus par Andrews sur 1 gramme de gaz carbonique, en commençant par des températures assez basses, pour obtenir le phénomène de condensation.

Partons par exemple d’un état \(M\) où le gaz occupe un volume très grand, sous une faible pression, à la température 0 °C et réduisons progressivement le volume en maintenant cette température à 0 °C.

La pression croît régulièrement et le point figuratif décrit l’arc d’isotherme \(MA'\), jusqu’à ce que soit atteint un volume \(u'\) (point figuratif \(A'\)) à partir duquel, bien que nous réduisions toujours le volume, la pression se refuse à décroître et reste égale à \(p\). Nous observons en même temps une condensation du gaz sous forme de gouttelettes de liquide qui se rassemblent au fond du récipient.

Réduisons toujours le volume. La proportion de liquide augmente et le gaz disparaît progressivement. Tant qu’il reste du gaz, la pression est égale à \(p\) et le point figuratif décrit l’horizontale ou palier \(AA'\), jusqu’au point \(A\) (volume \(u\)) où tout le gaz a disparu et où le récipient est empli de liquide.

Si nous continuons alors à réduire le volume à température constante, la pression monte rapidement et le point figuratif décrit l’arc d’isotherme \(AN\). L’arc \(AN\) est la branche liquide de l’isotherme, l’arc \(A'M\) la branche vapeur de l’isotherme, l’horizontale \(AA'\) est le palier de vaporisation de l’isotherme (ou de condensation).

Un point du palier \(AA\)’ tel que \(P\) représente un état du fluide partiellement liquide et partiellement gazeux. Tout au long du palier, les deux coordonnées thermodynamiques \(p\) et \(T\) gardent une valeur constante. Il en résulte que toutes les propriétés physiques du liquide et de la vapeur gardent des valeurs constantes, puisque l’état du liquide et celui de la vapeur sont parfaitement définis dès que les deux coordonnées \(p\) et \(T\) sont fixées. Seul varie le volume de l’ensemble du fait qu’une proportion plus ou moins grande du fluide est dans l’état vapeur.

Dans l’état \(A\), le fluide est entièrement sous forme liquide. Il porte le nom de liquide de saturation. Dans l’état \(A'\), il est entièrement sous forme de vapeur et porte le nom de vapeur saturante.

Dans un état tel que \(P\), le fluide est hétérogène : on le désigne sous le nom de mélange liquide – vapeur. Un tel mélange pourra être caractérisé par sa température et son titre \(x\) en vapeur : il s’agit du rapport de la masse de vapeur à la masse totale du mélange.

Nous avons pris ici une masse totale de 1 gramme de gaz carbonique. Le volume \(u\) est donc le volume spécifique du liquide de saturation à la température considérée, \(u'\) le volume spécifique de la vapeur saturante.

Cherchons alors le titre \(x\) du mélange de volume \(v\) représenté par le point \(P\). La masse de liquide que comprend ce mélange est \((1-x)\) grammes.

Les propriétés de ce liquide sont celles du liquide de saturation de volume spécifique \(u\) : son volume est donc \((1-x)~u\). La masse de vapeur présente dans le mélange est de \(x\) grammes. Les propriétés de cette vapeur sont celles de la vapeur saturante, de volume spécifique \(u'\). Son volume est donc \(x~u'\).

Le volume total du mélange est donc : \[v~=~(1-x)~u~+~x~u'\]

et \(x\) est donné par la relation : \[x~=~\frac{v-u}{u'-u}~=~\frac{AP}{AA'}\]

Recommençons la même expérience à une température plus élevée (20 °C par exemple). Le palier est obtenu pour une pression plus forte. L’isotherme a la même allure, mais le volume spécifique \(u\) du liquide de saturation a augmenté tandis que le volume spécifique de la vapeur saturante a diminué.

Point critique

Le palier s’est donc réduit et si nous élevons la température, il arrive que pour une certaine température dite température critique du gaz (environ 31 °C), le palier se réduit à un point, appelé point critique, qui constitue pour l’isotherme un point d’inflexion à tangente horizontale.

L’état du fluide (ici le gaz carbonique) représenté par le point \(C\) est appelé l’état critique. On dit aussi que le fluide est dans les conditions critiques : pression égale à la pression critique \(P_c\), volume égal au volume critique \(V_c\) (pour la masse de fluide considérée ici de 1 gramme), température égale à la température critique \(T_c\).

Aux températures supérieures à la température critique, les isothermes ne présentent plus de palier de condensation : il est donc impossible de liquéfier le gaz par compression isotherme à une température supérieure à la température critique.

Tous les gaz présentent cette propriété de ne plus être liquéfiables par compression au-dessus d’une température dite critique. La valeur de la température critique dépend évidemment de la nature du gaz :

– Pour le gaz carbonique, elle est de 31 °C et le gaz carbonique est donc liquéfiable par compression à la température ambiante, soit 15 °C par exemple.

– Pour l’oxygène, la température critique est de –119 °C ; il est donc impossible de liquéfier l’oxygène, quelle que soit la pression, à la température ordinaire. Il faudra au préalable abaisser sa température au-dessous de –119 °C, par exemple par une détente adiabatique réversible, et maintenir cette température pendant la compression.

2.1. Courbe de saturation

Le lieu des extrémités \(A\) et \(A'\) des divers paliers de vaporisation est une branche dite courbe de saturation, formée de deux branches se raccordant tangentiellement au point critique \(C\). La branche de gauche, lieu de \(A\), est la branche liquide de la courbe de saturation ; la branche de droite, lieu de \(A'\) est la branche vapeur de la courbe de saturation.

Notons qu’un point figuratif à l’extérieur de la courbe de saturation représente un état d’équilibre du fluide homogène, parfaitement défini par sa pression, son volume et sa température.

Un état hétérogène représenté par un point \(P\) à l’intérieur de la courbe de saturation est également défini par sa pression, son volume, sa température et le titre \(x\) du mélange liquide – vapeur, ces diverses coordonnées ne sont d’ailleurs pas indépendantes.

2.2. Continuité de l’état fluide

Il semble naturel de dire que le point \(M\) par exemple, représente un état gazeux, en d’autres termes une vapeur, puisque le fluide pris dans l’état \(M\) peut être condensé avec apparition de liquide par simple compression isotherme.

De même, un état tel que \(N\) devrait, semble-t-il être considéré comme un état liquide, puisqu’une détente isotherme du fluide pris dans l’état \(N\) l’amène à ébullition (en \(A\)).

Mais faisons subir au gaz pris dans l’état \(M\) un échauffement à volume constant qui amène à l’état \(N'\), suivi d’un refroidissement à pression constante qui l’amène à l’état \(N\). Nous n’avons observé au cours de l’opération aucune trace de condensation et pensons donc toujours avoir affaire à une vapeur ; cependant par détente isotherme cette prétendue vapeur va se mettre à bouillir.

On ne peut donc vraiment affirmer que le fluide est ici à l’état liquide, là à l’état vapeur, puisqu’il est possible de passer de façon continue d’un état à l’autre, sans que les propriétés du fluide aient jamais suivi de variation brusque.

L’état liquide n’est donc pas à proprement parler distinct de l’état gazeux, pas plus qu’il n’est distinct, comme nous le verrons plus tard, de l’état solide vitreux.

Ces trois états - liquide, gazeux et solide vitreux - font partie de l’ensemble commun des états amorphes de la matière que nous pourrons opposer à un autre état, fondamentalement distinct celui-là, l’état cristallin.

2.3. Courbe de pression de vapeur

Nous avons vu qu’à chaque isotherme dont la température est inférieure à la température critique correspond un palier de vaporisation où la pression est bien déterminée et ne dépend pas des masses de liquide et de vapeur à l’équilibre.

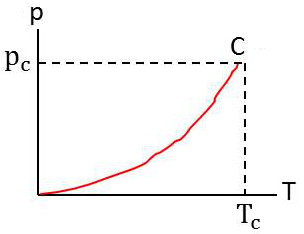Cette pression d’équilibre entre le liquide et la vapeur est désignée sous le nom de pression de vapeur saturante ou tout simplement de pression de vapeur du fluide à la température \(T\).

La pression \(P\) n’est fonction que de \(T\), et la courbe représentant \(P(T)\) présente l’allure ci-contre. Elle s’arrête à la température critique sans présenter de particularités en ce qui concerne ce point.

Les dérivées \(dP/dT\) et \(d^2P/dT^2\) notamment ne sont ni nulles ni infinies au point critique.

3. Écarts à la loi de Joule

Nous avons déjà remarqué que l’expérience de Joule – Gay-Lussac était trop peu sensible pour mettre en évidence un faible écart à la loi de Joule. Ceci a conduit Joule et Kelvin à imaginer une expérience nettement différente.

Le gaz y subit toujours une détente irréversible, mais l’utilisation d’un régime permanent élimine l’influence de l’inertie calorifique des accessoires dont la température est invariable ; l’expérience est beaucoup plus sensible.

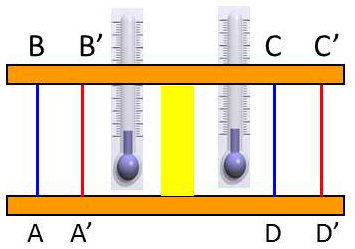
L’appareil se réduit à un tube à parois calorifugées dont la partie centrale est obstruée par une bourre de coton. Le freinage par le tampon de coton provoque une chute de pression.

En régime permanent, le gaz a la pression \(P_0\), la température \(T_0\) (mesurée au thermomètre à mercure) et un volume spécifique \(V_0\).

Il a la pression \(P < P_0\), la température \(T\) et le volume spécifique \(V'\) après traversée du tampon de coton.

Considérons un intervalle de temps pendant lequel une masse de 1 gramme de gaz a franchi le tampon de coton, la tranche de gaz située initialement en \(AB\) est passée en \(A'B'\). Celle qui était en \(CD\) est passée en \(C'D'\).

Le volume de gaz \(ABA'B'\) a une masse de 1 gramme. Il est égal au volume spécifique \(V_0\). Le volume \(CDC'D'\) est égal à \(V'\).

Cherchons à évaluer la différence d’énergie interne du gaz contenu dans \(CDC'D'\) et du gaz contenu dans \(ABA'B'\). Dans ce but, considérons la masse de gaz contenue initialement dans le volume \(ABCD\) ; elle est passée en \(A'B'C'D'\) en recevant une chaleur nulle et un travail : \[W=P_0~V_0-P~V'\]

Nous avons donc : \[U(A'B'C'D')-U(ABCD)~=~P_0~V_0-P~V'\]

Mais les masses \(ABCD\) et \(A'B'C'D'\) contiennent une partie commune dont l’énergie interne ne change pas lors de l’écoulement permanent, à savoir la partie \(A'B'CD\).

Nous pouvons donc remarquer que la variation d’énergie interne entre \(A'B'C'D'\) est due uniquement à la différence d’énergie interne des sections \(ABA’B’\) et \(CDC'D'\) et écrire : \[U(CDC'D')-U(ABA'B')~=~P_0~V_0-P~V'\]

Pour 1 gramme de gaz passant de l’état \([P_0,~V_0,~T_0]\) à l’état \([P,~V',~T]\)  : \[U(P,~V',~T)-U(P_0,~V_0,~T_0)=P_0~V_0-P~V'\]

Ou encore : \[H(P,~V',~T)-H(P_0,~V_0,~T_0)=0\]

On a donc introduit la fonction \(H\) désignée sous le nom d’enthalpie du gramme du gaz considéré.

L’enthalpie du gaz ne varie donc pas dans la détente Joule-Kelvin.

Mais nous nous intéressons principalement à la variation d’énergie interne dans une détente isotherme et nous allons chercher à comparer à \(U(P_0,~V_0,~T_0)\), non pas l’énergie interne \(U(P,~V',~T)\), mais l’énergie interne qu’aurait le gramme de gaz dans un état où sa pression aurait varié de \(P_0\) à \(P\), la température restant égale à \(T_0\) ; le volume serait alors passé à la valeur \(V\).

Cherchons donc à mesurer la variation d’énergie interne lorsque le gaz passe de l’état \([P_0,~V_0]\) à l’état \([P',~V]\) à la température constante \(T_0\). Pour cela, il nous suffit de ramener à pression constante \(P\) le gaz de l’état \([P,~V',~T]\) à l’état \([P,~V,~T]\).

Au cours de cette opération, le gramme de gaz reçoit une quantité de chaleur \(C_p~\theta\) , (\(\theta\) étant le refroidissement \(T_0-T\) qu’a subi le gaz dans la détente Joule–Kelvin) et un travail \(P~(V'-V)\) .

Nous écrirons donc : \[U(P,~V,~T_0)-U(P,~V',~T)=P~(V'-V)+C_p~\theta\]

Soit en définitive : \[U(P,~V,~T_0)-U(P_0,~V_0,~T_0)=P_0~V_0-P~V-C_p~\theta\]

Que nous pouvons aussi écrire : \[H(P,~V,~T_0)-H(P_0,~V_0,~T_0)=C_p~\theta\]

Le refroidissement \(\theta\) du gaz dans la détente Joule-Kelvin constitue l’un des critères de l’imperfection du gaz. On peut immédiatement vérifier qu’il serait nul pour un gaz parfait suivant les lois de Joule et de Mariotte ; il est en général différent de zéro pour un gaz réel.

Dans les conditions usuelles de température et de pression, on observe un refroidissement par détente Joule-Kelvin pour la grande majorité des gaz réels. Dans certains cas exceptionnels (hydrogène par exemple) on observe un faible échauffement \(\theta<0\). Voyons les conclusions que nous pouvons en tirer en ce qui concerne les écarts à la loi de Joule, en écrivant : \[U(P,~V,~T_0)-U(P_0,~V_0,~T_0)=P_0~V_0-P~V-C_p~\theta\]

a) Cas de l’hydrogène

Hypothèse des conditions usuelles de température et de pression

Le premier terme du second membre est positif et faible (\(H_2\) moins compressible que le gaz parfait), le second négatif (échauffement) mais encore plus faible en valeur absolue.

Nous en déduisons que : \(H(P,~V,~T_0)>H(P_0,~V_0,~T_0)\)

L’énergie interne de l’hydrogène croît avec le volume à température constante (rappelons que nous nous restreignons au domaine usuel de températures et de pressions).

b) Cas de la majorité des gaz réels

Hypothèse des conditions usuelles de température et de pression

Le premier terme du second membre est négatif (gaz plus compressible que les gaz parfaits), le second positif (refroidissement) mais c’est maintenant le second qui l’emporte, étant plus grand en valeur absolue.

On a donc encore : \(H(P,~V,~T_0)>H(P_0,~V_0,~T_0)\)

Nous en concluons donc que dans les conditions usuelles de température et de pression, l’énergie interne d’un gaz réel augmente quand son volume croît à température constante.

Remarque

Si le gaz qui subit la détente Joule-Kelvin est un gaz parfait, la loi de Joule exige : \[H(P,~V,~T_0)~=~H(P_0,~V_0,~T_0)\]

Et la loi de Mariotte exige que : \[P~V~=~P_0~V_0\]

Il en résulte que \(\theta~=~0\).

La température d’un gaz parfait ne varie donc pas lors de la détente de Joule-Kelvin.

Considérons par ailleurs, pour un fluide quelconque, l’expression générale de la différentielle de l’enthalpie (variation dans une transformation élémentaire) :

\[\begin{aligned} &dH~=~d(U+P~V)~=~dU~+~P~dV~+~V~dP\\ &dH~=~C_p~dT~+~h~dP~-~P~dV~+~P~dV~+~V~dP\\ \text{C'est-à-dire~:}\\ &dH~=~C_p~dT~+~(h+v)~dP\end{aligned}\]

D’où l’on tire : \[\Big(\frac{\partial H}{\partial P}\Big)_T=h+V\quad;\quad\Big(\frac{\partial H}{\partial T}\Big)_P=C_p\]

Pour un gaz parfait : \[\Big(\frac{\partial H}{\partial P}\Big)_T=0\qquad\text{d'où}\quad h=-V\]

On démontre enfin que pour les expressions de l’énergie interne et de l’enthalpie d’un gaz parfait quelconque :

\[\begin{aligned} &U~=~U_0+\int_{T0}^T C_V~dT\\ &H~=~H_0+\int_{T0}^T C_P~dT\end{aligned}\]

\(U_0\) et \(H_0\) étant les valeurs arbitrairement choisies pour \(U\) et \(H\) à la température \(T_0\).