1. Introduction

Une même substance pure peut, dans certaines conditions de température et de pression, former plusieurs phases distinctes. Par exemple, un fluide dont le point figuratif, dans le diagramme de Clapeyron, se trouve à l’intérieur de la courbe de saturation, se présente (sauf évidemment dans le cas où il s’agirait d’un équilibre métastable) en partie sous forme d’une phase gazeuse, les deux phases liquide et gazeuse en équilibre ayant la même température et la même pression.

Toutes les substances pures peuvent, tout au moins dans un certain domaine de températures et de pressions, se présenter sous forme solide, liquide ou gazeuse. Une substance solide peut, en outre, se présenter sous diverses variétés allotropiques qui constituent autant de phases distinctes (par exemple étain blanc et étain gris).

Supposons qu’à une certaine température \(T\) et à une certaine pression \(p\), la substance puisse se présenter sous forme de deux phases distinctes. Nous désignerons sous le nom de changement de phase, la transformation conduite à pression et température constantes au cours de laquelle la substance, initialement rassemblée en entier dans l’une des phases, passe progressivement dans l’autre.

Le changement d’état thermodynamique subi par la substance est défini par la seule connaissance des états de départ et d’arrivée ; l’appellation changement de phase implique en outre que la transformation a lieu à température et pression constantes.

Par exemple, une vapeur saturante passant à l’état liquide de saturation en contournant par le haut le point critique dans le diagramme de Clapeyron ne subit pas, d’après cette définition, un changement de phase puisque \(p\) et \(T\) sont restées constantes, bien qu’elle subisse en définitive le même changement d’état thermodynamique.

2. Changement de phase

Tous les changements de phase que nous avons considérés jusqu’à présent (fusion, vaporisation, sublimation, modification allotropique) présentent deux caractéristiques communes :

1) Un transfert de chaleur se produit entre la substance et le thermostat qui la maintient à température constante. Le changement de phase peut être conduit de façon réversible, ce transfert de chaleur est lié à une différence d’entropie entre la phase initiale et la phase finale.

Supposons que la masse de la substance soit égale à l’unité de masse ; désignons par les indices \((i)\) et \((f)\) les quantités relatives à la phase initiale et à la phase finale, respectivement.

La quantité de chaleur échangée avec le thermostat porte le nom de chaleur latente de transformation ou de changement de phase. On peut écrire en la désignant par \(L\) : \[L=T~(S_f-S_i)\]

• \(T\) : température de changement de phase à la pression \(p\) considérée

• \(S_i,~S_f\) : entropies initiale et finale

2) Le changement de phase s’accompagne d’un changement de volume, soit \(v_f\neq v_i\) .

Nous réservons le nom de changement de phase à de telles transformations que nous pourrons désigner aussi sous le nom de transitions de première espèce par opposition à d’autres transformations qui se produisent en phase homogène et que nous étudierons plus loin.

2.1. Formule de Clapeyron

Le changement de phase étant isotherme, isobare et réversible, la fonction de Gibbs de la substance est invariante : \[G_f(p,~T)=G_i(p,~T)\]

Nous savons par ailleurs que, pour toute modification de l’état de la phase \((i)\) (ne faisant pas apparaître la phase \((f)\) : \[dG_i=v_i~dp-S_i~dT\]

De même pour toute modification de l’état de la phase \((f)\) (ne faisant pas apparaître la phase \((i)\) : \[dG_f=v_f~dp-S_f~dT\]

Considérons alors le même changement de phase effectué à la pression \(p+dp\)  ; la température du changement de phase est alors \(T+dT\) et l’on peut écrire : \[G_f(p+dp,~T+dT)=G_i(p+dp,~T+dT)\]

En comparant avec l’équation écrite pour les conditions \(p\) et \(T\) : \[dG_i=dG_f\]

C’est à dire : \[v_fdp-S_f~dT=v_i~dp-S_i~dT\]

Ou encore : \[\frac{dp}{dT}=\frac{S_f-S_i}{v_f-v_i}\]

\(dp/dT\) est la pente de la courbe \(f(T)\) liant la pression et la température de changement de phase.

En comparant à \(L=T~(S_f-S_i)\), nous obtenons la formule de Clapeyron : \[L=T~(v_f-v_i)~\frac{dp}{dT}\]

2.2. Caractéristiques des changements de phase de première espèce

Les expressions de \(dG_i\) et \(dG_f\) indiquent que :

\[\begin{aligned} &S_i=\Big(\frac{\partial G_i}{\partial T}\Big)_p\qquad;\qquad v_i=\Big(\frac{\partial G_i}{\partial p}\Big)_T\\ &S_f=\Big(\frac{\partial G_f}{\partial T}\Big)_p\qquad;\qquad v_f=\Big(\frac{\partial G_f}{\partial p}\Big)_T\end{aligned}\]

La présence d’une chaleur latente de transformation et d’une variation de volume exige donc que :

\[\begin{aligned} &\Big(\frac{\partial G_f}{\partial T}\Big)_p~\neq~\Big(\frac{\partial G_i}{\partial T}\Big)_p\\ &\Big(\frac{\partial G_f}{\partial p}\Big)_T~\neq~\Big(\frac{\partial G_i}{\partial p}\Big)_T\end{aligned}\]

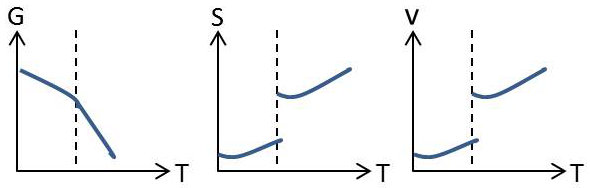Il en résulte que, la pression étant maintenue constante, la substance traverse la température de changement de phase à la pression considérée, les dérivées partielles de sa fonction de Gibbs subissent une discontinuité.

La figure ci-contre indique l’allure des variations de \(G\), \(S\) et \(v\) en fonction de \(T\) dans un changement de phase de première espèce.

2.3. Conséquences immédiates de la formule de Clapeyron

La formule de Clapeyron indique que, si le changement de phase s’accompagne d’une augmentation de volume, \(dp/dT\) est du signe de \(L\).

Exemples

– Dans les phénomènes de vaporisation et de sublimation, la phase finale est une phase gazeuse, de volume bien plus grand que celui de la phase initiale liquide ou solide. Par ailleurs, le changement de phase s’accompagne toujours d’une absorption de chaleur.

La pente \(dp/dT\) de la courbe donnant la pression d’équilibre entre phases en fonction de la température est donc toujours positive. La température à laquelle a lieu le changement de phase est d’autant plus élevée que la pression est plus forte.

– La fusion est également un phénomène s’accompagnant d’une absorption de chaleur. Si la fusion entraîne une augmentation de volume, ce qui a lieu dans la majorité des cas, \(dp/dT\) est toujours positif. Si elle s’accompagne au contraire d’une contraction (cas de l’eau par exemple au voisinage de la pression atmosphérique), \(dp/dT\) est négatif.

On remarquera d’autre part que les chaleurs latentes de fusion sont du même ordre de grandeur que les chaleurs latentes de vaporisation ou de sublimation alors que la variation de volume est bien plus faible dans le phénomène de fusion que dans les deux autres.

La pente \((dp/dT)_f\) de la courbe de fusion est donc plus accentuée que les pentes \((dp/dT)_v\) et \((dp/dT)_S\) des courbes de vaporisation et de sublimation.

2.4. Point triple

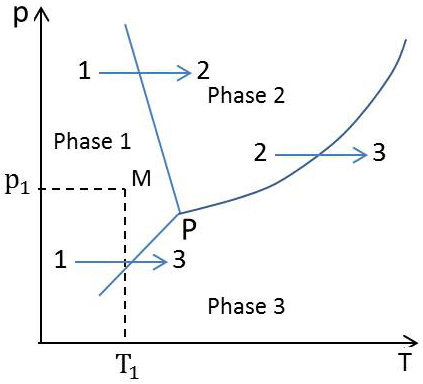Désignons par les indices 1, 2, 3 trois phases distinctes sous l’aspect desquelles peut se présenter une substance donnée.

Nous pouvons à chaque pression noter la température à laquelle se produit le changement de phase \(1\rightarrow 2\) et la température à laquelle se produit le changement de phase \(2\rightarrow 3\), et porter sur un diagramme ces températures de transformation en fonction de la pression de la transformation.

Nous obtenons deux courbes qui se coupent en un point P. Chacune des courbes correspond à l’équilibre thermodynamique entre les phases en présence, en l’occurrence les phases 1 vers 2 pour la première, 2 vers 3 pour la seconde (un tel équilibre est en effet nécessaire pendant la durée du changement de phase qui se produit de façon réversible à \(T\) et \(p\) constantes).

La courbe d’équilibre 1 – 2 traduit, dans le diagramme \((p,~T)\) la relation qui doit exister entre \(T\) et \(p\) pour que l’unité de masse (par exemple) de la substance considérée ait même fonction de Gibbs, qu’elle soit sous la forme de la phase 1 ou sous la forme de la phase 2, soit : \[G_1(p,~T)=G_2(p,~T)\]

De même, la courbe d’équilibre 2 – 3 est le lieu des points \((p,~T)\) tels que : \[G_2(p,~T)=G_3(p,~T)\]

S’il existe un point d’intersection des courbes d’équilibre 1 – 2 et 2 – 3, ce point est donc tel que : \[G_1(p,~T)=G_2(p,~T)=G_3(p,~T)\]

Il est donc situé sur la courbe d’équilibre 1 – 3. Les trois courbes d’équilibre 1 – 2, 1 – 3, 2 – 3 concourent donc en un point \(P\) que l’on désigne sous le nom de point triple.

La région du diagramme entourant le point triple est séparée par les trois courbes en trois domaines à l’intérieur desquels la substance ne peut exister en équilibre stable que sous l’une des trois phases.

Considérons par exemple la région de stabilité de la phase 1 et soit \(M\), de coordonnées \(p_1,~T_1\), un point pris dans cette région. Il est possible que, par suite des phénomènes de retard aux changements de phase, la substance puisse exister à la pression \(p_1\) et à la température \(T_1\) sous forme de la phase 2 ou de la phase 3, mais elle sera alors en équilibre métastable ; ce qui signifie qu’un germe infinitésimal de la phase 1 suffira à provoquer, \(p\) et \(T\) étant maintenues à \(p_1,~T_1\) constantes, la transformation complète de la substance sous forme de la phase 1.

Cette transformation irréversible à \(p\) et \(T\) extérieures imposées, exige une diminution de la fonction de Gibbs ; il en résulte que pour tout couple de valeurs \((p_1,~T_1)\) pris dans la région de stabilité de la phase 1 on a :

1. \(G_1(p_1,~T_1) < G_2(p_1,~T_1)\) si la substance peut exister sous forme de phase 2 (liquide) en équilibre métastable dans les conditions \((p_1,~T_1)\) ;

2. \(G_1(p_1,~T_1) < G_3(p_1,~T_1)\) si la substance peut exister sous forme de phase 3 (vapeur) dans les conditions \((p_1,~T_1)\).

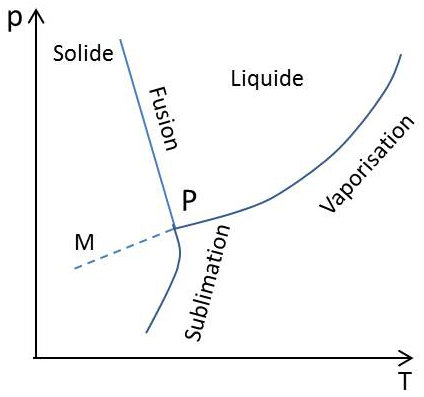
La figure ci-contre correspond au cas classique du point triple solide – liquide – vapeur, se dilatant par fusion. Dans le cas de l’eau, la pente de la courbe de fusion est négative (disposition analogue à celle de la figure précédente).

2.5. Point triple solide – liquide – vapeur

La pente de la courbe de fusion (généralement positive) est beaucoup plus grande en valeur absolue que celle des courbes de vaporisation et de sublimation.

À une pression supérieure à celle du point triple, une élévation de température entraîne toujours le phénomène de fusion (jamais de retard à la fusion), puis le phénomène de vaporisation qui peut présenter un certain retard (état métastable).

Si par contre, partant de l’état de vapeur, on abaisse la température, on observe successivement les phénomènes de condensation (retard éventuel) et de solidification (retard éventuel).

Si la pression est inférieure à celle du point triple, on observe, par échauffement du solide, le phénomène de sublimation (pas de retard), par refroidissement de la vapeur le passage direct de la phase vapeur à la phase solide. Cependant, le dernier passage peut se trouver retardé en l’absence de germes cristallins de la phase solide.

On se trouve alors en présence d’une vapeur en équilibre qui peut se transformer en liquide de façon réversible lorsque le point figuratif traverse le prolongement au-dessous du point triple de la courbe de vaporisation.

Ce phénomène va nous permettre de montrer que la pente de la courbe de vaporisation au point triple est certainement inférieure à la pente de la courbe de sublimation ; il nous suffit pour cela de démontrer que le prolongement de la courbe de vaporisation au-dessous du point triple est située au-dessus de la courbe de sublimation. À cet effet, considérons un point \(M(p,~T)\) pris sur le prolongement de la courbe de vaporisation au-dessous du point triple.

Pour ces conditions de température et de pression, la phase liquide (liquide surfondu) est moins stable que la phase solide, on a donc : \[G_{sol}(p,~T)<G_{liq}(p,~T)\]

L’équilibre des phases vapeur et liquide exige que : \[G_{vap}(p,~T)<G_{liq}(p,~T)\]

On a donc : \[G_{sol}(p,~T)<G_{vap}(p,~T)\]

La vapeur est également en équilibre métastable par rapport au solide (ce qui signifie que l’introduction d’un cristal du solide de dimensions infinitésimales entraînerait la rupture de cet équilibre et la solidification de l’ensemble).

Le point \(M\) se trouve donc dans la région de stabilité de la phase solide, c’est à dire entre les courbes de fusion et de sublimation.

2.6. Relations entre les chaleurs latentes en un point triple

Soient \(1,~2,~3\) les 3 phases en équilibre, \((L_{1\rightarrow 2},~L_{1\rightarrow 3},~L_{2\rightarrow 3})\) les chaleurs latentes correspondant aux trois changement de phase que l’on peut y envisager à \(p\) et \(T\) constantes.

Ces transformations étant isobares et le système n’étant sensible qu’aux forces de pression, on peut écrire les chaleurs latentes comme variations d’enthalpies :

\[\begin{aligned} &L_{1\rightarrow 2}=H_2-H_1\\ &L_{1\rightarrow 3}=H_3-H_1\\ &L_{2\rightarrow 3}=H_3-H_2\end{aligned}\]

Nous en tirons immédiatement : \[L_{1\rightarrow 3}=L_{1\rightarrow 2}+L_{2\rightarrow 3}\]

Avec une application importante : \[L_{sub}=L_{fus}+L_{vap}\]

2.7. Expression simplifiée des chaleurs latentes de vaporisation et sublimation

Supposons que la pression choisie soit très inférieure à la pression critique de la substance. Nous pourrons alors assimiler la vapeur à un gaz parfait et négliger les volumes spécifiques du liquide et du solide devant celui de la vapeur.

En désignant par \(L_v\) et \(L_s\)les chaleurs latentes de vaporisation et de fusion, par \(p_{vap}(T)\) la pression de vaporisation à la température \(T\), par \(u'\) le volume spécifique de la vapeur, nous pourrons écrire : \[L_v\approxeq T~u'~\frac{dP_{vap}}{dT}\approxeq\frac{T}{M}~\frac{R~T}{P_{vap}}~\frac{dP_{vap}}{dT}=\frac{R~T^2}{M}~\frac{d(\ln P_{vap})}{dT}\]

D’où il vient : \[\frac{d(\ln P_{vap})}{dT}\approxeq\frac{M~L_v}{R~T^2}\]

Et de la même façon : \[\frac{d(\ln P_s)}{dT}\approxeq\frac{M~L_s}{R~T^2}\]

Insistons sur le fait que ce serait une grosse erreur que de vouloir appliquer ces formules à la vaporisation d’un fluide au voisinage du point critique, les propriétés de la vapeur s’écartant alors considérablement de celles d’un gaz parfait.

2.8. Fusion et solidification

La courbe de fusion sépare en principe le domaine du liquide du domaine du solide. Toutefois, prenons une substance qui se dilate par fusion (c’est le cas de l’eau aux très hautes pressions). Si nous élevons la pression de plusieurs milliers d’atmosphères, la température de fusion peut dépasser la température critique de la substance considérée. L’état obtenu par fusion peut aussi bien être considéré comme un gaz que comme un liquide.

En fait, les courbes de fusion et de sublimation séparent l’état cristallin de l’état amorphe (liquide ou gazeux) ; il s’agit bien là d’un changement radical de la matière s’accompagnant obligatoirement d’un changement discontinu de ses propriétés.

Il est impossible en effet de passer de l’état solide cristallisé à l’état liquide, comme on avait pu le faire pour le passage du liquide au gaz, en contournant par le haut un point critique et en évitant ainsi tout changement de phase. La courbe de fusion s’étend indéfiniment vers les hautes pressions et les hautes températures, sans s’arrêter en un point critique comme c’était le cas pour la courbe de vaporisation.

Il est clair d’ailleurs qu’il serait impossible de concevoir le passage continu d’une substance de l’état ordonné que constitue un cristal à l’état désordonné de la matière amorphe (rappelons que nous devrions supposer la substance homogène à chaque instant). Ce passage est effectivement impossible. La fusion est un phénomène essentiellement discontinu, le passage de l’ordre au désordre entraînant d’ailleurs un accroissement d’entropie, d’où la chaleur de fusion.

Le phénomène de fusion se produit lorsque l’agitation thermique devient suffisante pour briser les forces de liaison qui maintiennent les atomes (ou les ions) en des positions définies. Il ne saurait donc souffrir aucun retard.

Par contre, le phénomène inverse de solidification se produit en général avec un certain retard. Il faut en effet pour que le cristal se forme, une fois la température assez basse, que quelques atomes se trouvent en position convenable pour amorcer un début de réseau cristallin régulier ; si la substance est parfaitement exempte de toute particule cristalline, seul le hasard pourra entraîner la formation d’un tel germe spontané.

Le liquide a donc tendance à rester en état de surfusion. On fera généralement cesser la surfusion en projetant dans le liquide surfondu une parcelle infime de substance cristallisée, qui joue alors le rôle de germe. En l’absence d’aide extérieure, il faut que deux conditions soient réunies pour qu’apparaisse la cristallisation :

1. des germes doivent être présents ;

2. ces germes doivent se développer.

Or, il peut arriver que des germes ne se forment spontanément qu’à une température beaucoup plus basse qu’à la température de fusion, et que, par contre, ils ne puissent se développer qu’à une température qui ne soit pas trop inférieure à celle de la fusion. On se trouve alors dans le cas suivant :

Par refroidissement du liquide, on arrive bien, un peu au-dessous de la température de fusion, dans une région où les germes pourraient se développer rapidement, mais aucun germe n’est présent et la substance reste à l’état liquide.

Abaissons encore la température ; des germes se forment, mais la température est maintenant trop basse pour qu’ils puissent se développer ; nous pourrons alors abaisser la température jusqu’au zéro absolu sans que la cristallisation se produise.

Le liquide devient tellement visqueux qu’il a les propriétés mécaniques de l’état solide. On se trouve en présence d’un solide vitreux. Le verre ordinaire, qui n’est en somme qu’un liquide fortement surfondu, en est le meilleur exemple. Cependant, ce solide vitreux a traversé la région de formation rapide des germes et en contient donc un grand nombre.

Si, par inadvertance, nous le réchauffons à la température voisine de la température de fusion, où les germes pourront se développer, il va se cristalliser rapidement, c’est ce qui se passe lorsqu’un souffleur de verre inexpérimenté réchauffe plusieurs fois un tube qu’il n’arrive pas à former rapidement : le verre cristallise, devient opaque, fragile et inutilisable.

Citons comme exemple important de surfusion, la formation dans l’atmosphère de nuages givrants composés de gouttelettes d’eau surfondue, qui se congèlent au contact d’un obstacle en le recouvrant rapidement d’une épaisse couche de glace, gênante sur un pare-brise de voiture, mais catastrophique sur une aile d’avion.

2.9. États mésomorphes

Le passage de l’état cristallin, ordonné dans les trois dimensions, à l’état amorphe liquide, peut, dans certains cas, se faire par degrés ; on obtient ainsi des états mésomorphes, intermédiaires entre l’état cristallin et l’état liquide. Ces états sont d’ailleurs parfaitement définis et ne constituent en aucune manière une jonction continue entre l’état cristallin et l’état liquide.

On en distingue deux :

1) Dans l’état smectique, les molécules (il s’agit toujours de molécules à longue chaîne) s’arrangent en couches parallèles d’épaisseur constante (40 à 50) qui peuvent glisser les unes sur les autres, et à l’intérieur desquelles les molécules ont perdu leur arrangement régulier bidimensionnel, mais restent cependant parallèles à elles-mêmes. Une molécule ne se déplace donc que dans le plan de sa couche et non dans les trois dimensions.

Les rayons \(X\) ont permis de vérifier la régularité d’épaisseur de ces couches, le microscope électronique a permis d’observer la structure en gradins des gouttes obtenues en déposant la substance sur une plaque de verre.

2) Dans l’état nématique, les molécules se déplacent librement dans les trois dimensions, mais en restant parallèles à elles-mêmes. Il en résulte une anisotropie, notamment optique, qui permet de distinguer la substance d’un liquide ordinaire.

Seules certaines substances peuvent ainsi passer à l’état smectique et à l’état nématique. Le savon ordinaire est dans un état smectique. Les passages cristal-smectique, smectique-nématique et nématique-liquide, sont des changements de phase de première espèce, qui se produisent, la pression étant fixée, à une température bien déterminée.

2.10. Transformations allotropiques

On peut citer comme exemple de transformations allotropiques l’équilibre entre les diverses variétés de glace, le cas du soufre, celui de l’étain. L’étain ordinaire, blanc, n’est stable à la pression ordinaire qu’au dessus de 19 °C. Au-dessous, la variété stable est un étain gris pulvérulent.

Les objets en étain ne subissent cependant pas la transformation à 19 °C, car des germes sont nécessaires ; ces germes ne se produisent qu’à très basse température (optimum –48 °C). Si l’on porte alors un objet en étain un certain temps à une quarantaine de degrés au-dessous de zéro, il tombera en poussière lors d’un retour à 0 °C où la vitesse de transformation est maximum. C’est ainsi que l’on a pu observer la peste de l’étain après des hivers très rigoureux.

3. Changements d’état de seconde espèce

Certaines transformations à \(p\) et \(T\) constantes se produisent sans transfert de chaleur et sans variation de volume. Dans ces cas-là, les dérivées premières de la fonction de Gibbs varient donc de façon continue quand la substance traverse à pression constante, la température de transformation, mais leur courbe de variation présente un point anguleux à la température de transformation, ce qui indique, à la traversée de cette température, une discontinuité des dérivées secondes de la fonction de Gibbs.

De telles transformations portent le nom de changements d’états de seconde espèce ou de transitions de seconde espèce. Elles ne constituent pas à proprement parler un changement de phase, car l’on ne voit pas apparaître en cours de transformation la séparation de la substance en deux phases distinctes séparées par une surface de discontinuité.

On connaît assez peu d’exemples sûrs de tels changements d’état de seconde espèce. Il est évident qu’il est difficile d’affirmer qu’une chaleur latente est rigoureusement nulle et non pas simplement trop petite pour être mesurable ; de même, en ce qui concerne les variations de volume.

Quelques exemples :

• le passage de l’hélium liquide de la forme 1 à la forme 2, que nous étudierons un peu en détail, et qui constitue à peu près certainement un changement d’état de seconde espèce ;

• la traversée du point de Curie par une substance ferromagnétique qui devient paramagnétique ;

• le passage d’un métal de l’état conducteur à l’état supraconducteur, en l’absence d’excitation magnétique, à une température de transition bien définie ;

• les transformations ordre-désordre dans certains alliages ;

• etc.

Nous avons signalé la discontinuité des dérivées secondes de \(G\). Cette discontinuité se traduit expérimentalement par des variations des coefficients de dilatation et de compressibilité isotherme de la substance, ainsi que de sa chaleur spécifique \(C_p\), lorsqu’elle traverse la température de transformation.

On a en effet:

\[\begin{aligned} \frac{\partial^2G}{\partial T^2}&=-\Big(\frac{\partial S}{\partial T}\Big)_p=-\frac{C_p}{T}\\ \frac{\partial^2G}{\partial p^2}&=\Big(\frac{\partial v}{\partial p}\Big)_T=-\chi_v\\ \frac{\partial^2G}{\partial p~\partial T}&=\Big(\frac{\partial v}{\partial T}\Big)_p=\alpha~v\end{aligned}\]

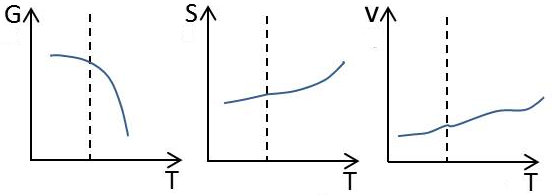Si nous désignons par les indices \((i)\) et \((f)\) les quantités relatives à l’état initial et à l’état final, nous avons donc (voir figure ci-contre) :

\[\begin{aligned} C_{pi}~&\neq~C_{pf}\\ \alpha_i~&\neq~\alpha_f\\ \chi_i~&\neq~\chi_f\end{aligned}\]

mais on aura: \[S_i=S_f\qquad;\qquad v_i=v_f\]

3.1. Équations d’Ehronfest

Envisageons le changement d’état de seconde espèce, conduit tout d’abord à la pression \(p\) (température de transition \(T\)), puis à la pression \(p+dp\) (température de transition \(T+dT\)). Nous pouvons écrire :

\[\begin{aligned} S_f(T,~p)&=S_i(T,~p)\\ S_f(T+dT,~p+dp)&=S_i(T+dT,~p+dp)\end{aligned}\]

D’où l’on tire: \[dS_f=dS_i\]

En remarquant que : \[\Big(\frac{\partial S}{\partial p}\Big)_T=-\frac{\partial^2G}{\partial T\partial p}=\Big(\frac{\partial v}{\partial T}\Big)_p\]

Il vient : \[C_{pf}~\frac{dT}{T}-v~\alpha_f~dp=C_{pi}~\frac{dT}{T}-v~\alpha_i~dp\]

Il s’ensuit que : \[\frac{dp}{dT}=\frac{1}{T~v}~\frac{C_{pf}-C_{pi}}{\alpha_f-\alpha_i}\qquad(1)\]

Or, nous pouvons aussi écrire :

\[\begin{aligned} v_f(T,~p)&=v_i(T,~p)\\ v_f(T+dT,~p+dp)&=v_i(T+dT,~p+dp)\end{aligned}\]

On en tire : \[dv_f=dv_i\]

Il vient alors : \[\alpha_f~v~dT-\chi_f~v~dp=\alpha_i~v~dT-\chi_i~v~dp\]

D’où l’on tire : \[\frac{dp}{dT}=\frac{\alpha_f-\alpha_i}{\chi_f-\chi_i}\]

Remarquons que l’équation (1) ci-dessus peut s’écrire : \[C_{pf}-C_{pi}=T~v~(\alpha_f-\alpha_i)~\frac{dp}{dT}\]

forme analogue à celle de Clapeyron qui se trouve donc remplacée par cette relation pour les changements d’état de seconde espèce.

4. Propriétés de l’hélium aux basses températures

Kamerlingh Onnes a remarqué en 1924 que l’hélium liquide présente, lorsqu’il traverse, en équilibre avec sa vapeur, la température 2,19 K, une anomalie du coefficient de dilatation qui subit une discontinuité : la densité croît bien par refroidissement jusqu’à 2,19 K, mais diminue ensuite jusqu’à 1,5 K.

Ceci suggère immédiatement qu’il y a un changement qui se produit alors dans la phase condensée bien qu’elle reste liquide ; ce changement a lieu sans discontinuité de volume et tous les essais de détection d’une chaleur latente de transformation ont échoué.

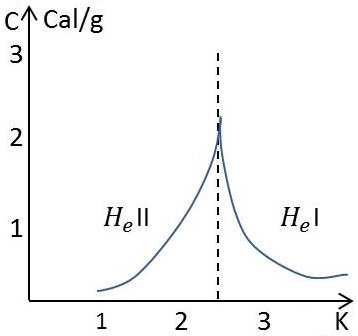On est donc en présence d’un changement d’état de seconde espèce de la phase liquide qui passe lors du refroidissement du liquide hélium I au liquide hélium II.

La courbe des chaleurs spécifiques de l’hélium en équilibre avec sa vapeur présente également une discontinuité importante à la température 2,19 K. L’ensemble de la courbe rappelle la forme d’un lambda majuscule, d’où le nom de transformation \(\lambda\) donné à ce changement d’état de l’hélium.

4.1. Quelques propriétés particulières à l’hélium

Pour tous les autres corps purs, il suffit d’abaisser suffisamment la température en maintenant le liquide en équilibre avec sa vapeur pour arriver à un point triple où se forme la phase solide. Ce n’est pas le cas pour l’hélium aux pressions usuelles ; il reste liquide jusqu’aux températures les plus basses et certainement jusqu’au zéro absolu. Il est cependant possible de solidifier l’hélium en opérant à une pression supérieure à 25 atmosphères.

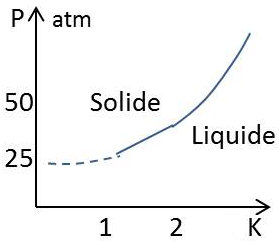La courbe de fusion de l’hélium (figure ci-contre) présente la curieuse propriété de devenir horizontale au-dessous de 1,15 K. Appliquons alors la formule de Clapeyron : \[L_f=T~(v_i-v_s)~\Big(\frac{dp}{dT}\Big)_f\]

On notera que : \[\Big(\frac{dp}{dT}\Big)_f\rightarrow 0 \quad\text{quand } T\rightarrow 0,\text{ donc}\quad L_f\rightarrow 0\]

Il n’y a plus de chaleur de fusion. Bien mieux : \[\frac{L_f}{T}\rightarrow 0\quad\text{et, par suite,}\quad (\Delta S)_{fusion}\rightarrow 0\]

L’entropie du liquide hélium II est la même que celle du solide au zéro absolu. D’où cette conclusion que le liquide est aussi ordonné que le solide au zéro absolu. Il apparaît alors que le liquide est la variété thermodynamique stable au zéro absolu au-dessous de 25 atmosphères, le solide étant la variété stable au-dessus de 25 atmosphères.

L’hélium est le seul corps possédant ces propriétés ; seul d’ailleurs, l’isotope \( ^4He\) les possède, l’isotope \( ^3He\) se comportant de façon normale.

Courbe d’équilibre dans le diagramme \(p,~T\)

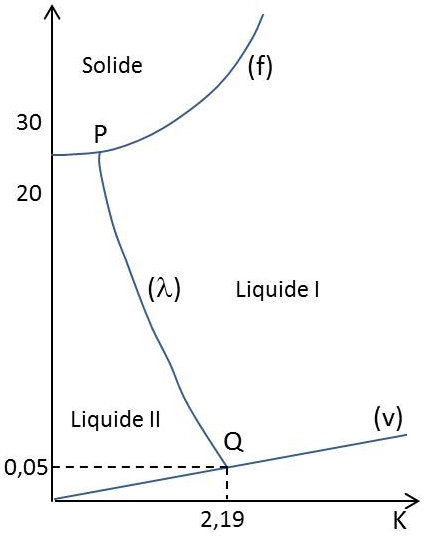La figure représente le diagramme d’équilibre. La courbe de fusion \((f)\) et la courbe de vaporisation \((v\)) sont reliées par la courbe \((\lambda)\) qui les atteint en deux point \(P\) et \(Q\).

À droite de la courbe\((\lambda)\), la phase liquide est de l’hélium I ; à gauche de l’hélium II.

Il faut bien noter que les courbes de fusion et de vaporisation ne présentent pas de points anguleux aux points \(P\) et \(Q\).

Si nous désignons en effet par les indices \(s,~v,~I,~II\) les quantités relatives au solide, à la vapeur, au liquide I et au liquide II, nous avons au point P :

– vers la gauche : \[\Big(\frac{dP}{dT}\Big)_{sol,~II}=\frac{S_s-S_{II}}{v_s-v_{II}}\]

– vers la droite : \[\Big(\frac{dP}{dT}\Big)_{sol,~I}=\frac{S_s-S_{I}}{v_s-v_{I}}\]

Comme on a \(S_{II}=S_I\) et \(v_{II}=v_I\), les pentes sont égales.

De même au point Q: \[\Big(\frac{dP}{dT}\Big)_{vap,~II}=\frac{S_v-S_{II}}{v_v-v_{II}}=\frac{S_v-S_I}{v_v-v_I} =\Big(\frac{dP}{dT}\Big)_{vap,~I}\]

4.2. Phénomènes de transfert

4.2.1. Transfert de chaleur

Le coefficient de conductibilité thermique de l’hélium I est normal. À 3,3 K, il vaut \(6,10^{15}\) cal/K.cm.s, c’est une valeur qui s’approche de ce que l’on observe pour un gaz à la température ordinaire.

Pour l’hélium II la conductibilité thermique est fantastique : son maximum (aux environs de 2 K) vaut 100 cal/K.cm.s, soit 300 fois la conductibilité du cuivre à la température ordinaire. L’hélium II apparaît comme un supraconducteur thermique.

4.2.2. Superfluidité

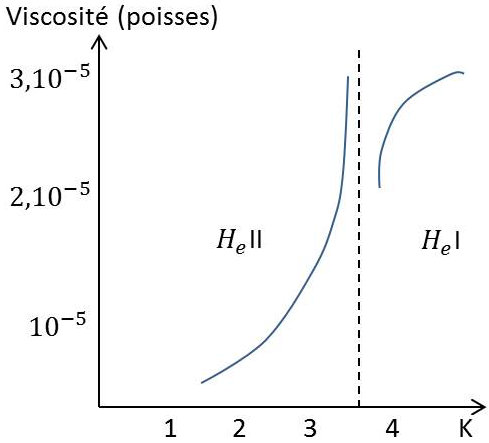La viscosité de l’hélium liquide présente des caractères surprenants. Mesurée par la méthode classique de l’amortissement d’un disque oscillant, elle s’abaisse avec la température, contrairement à ce qui se passe pour les liquides normaux.

L’abaissement est très rapide dès que l’on arrive à l’hélium II ; de plus, la viscosité est très faible en valeur absolue (voir figure ci-contre). Si on cherche à le mesurer par la vitesse d’écoulement dans un tube capillaire, on s’aperçoit qu’elle tombe au-dessous de toute valeur mesurable.

Tisza a pu donner une interprétation phénoménologique de ces faits en admettant que l’hélium se compose de deux fluides, l’un formé d’atomes normaux à viscosité normale, l’autre d’atomes superfluides capables de se déplacer au sein des autres, sans frottement ni viscosité.

Ces atomes superfluides formeraient à la surface du capillaire un film glissant sur elle sans frottement, d’où disparition des lois de la viscosité où l’on admet que la couche liquide au contact de la paroi reste immobile.

Dans la méthode du disque oscillant, le film n’aurait pas le temps de s’organiser complètement, du fait du renversement du sens du mouvement à chaque demi-période. On a pu, en empilant des disques oscillants à très faible distance l’un de l’autre, s’arranger pour que les atomes normaux situés entre les disques restent collés à eux, modifiant ainsi le moment d’inertie.

On peut en déduire la proportion d’atomes normaux contenus dans l’hélium II en fonction de la température. Cette proportion tend vers zéro au zéro absolu, vers 1 au point \(\lambda\) et varie très vite avec \(T\). Une élévation locale de température en un point du liquide II entraîne alors un glissement rapide des atomes superfluides que contenaient les régions froides vers cette région (vitesse de l’ordre de \(10^4~cm/s\) ). On conçoit alors que le coefficient de conductibilité thermique soit gigantesque. Il s’agit plus de transport de matière que de chaleur.

4.2.3. Film de Rollin

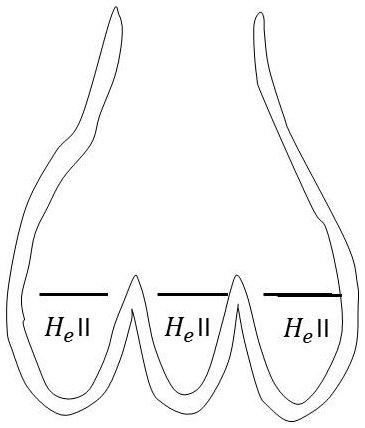Rollin a observé en 1936 que l’évaporation de l’hélium II dans un vase Dewar est beaucoup plus rapide que celle de l’hélium I. Il se forme en effet un film de liquide II qui recouvre complètement les parois du vase, ce qui accroît évidemment l’évaporation.

On peut mesurer l’épaisseur de ce film en le répandant sur de grandes surfaces et mesurant la baisse de niveau correspondante dans le vase (20 à 30 nm).

Ce film permet de faire fluir l’hélium II par siphonage du récipient qui le contient ou d’égaliser les niveaux dans le vase double. La vitesse d’écoulement est indépendante du niveau dès qu’il dépasse 1 cm, elle est de l’ordre de 20 à 30 cm/s.

4.2.4. Effet fontaine

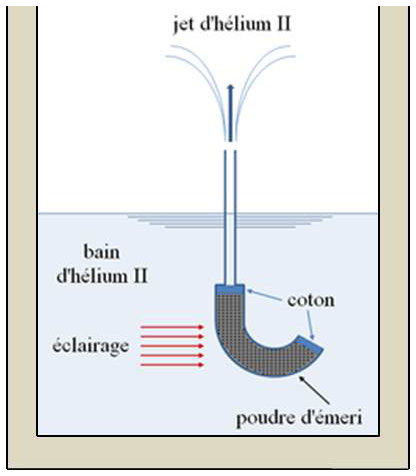À l’intérieur d’un vase Dewar contenant de l’hélium II est placé un petit récipient percé dans le bas et surmonté d’un capillaire. À l’intérieur de ce récipient est placée de la poudre d’émeri. On illumine cette poudre d’émeri avec un rayonnement infrarouge qu’elle absorbe.

La température intérieure du récipient s’élève et il en résulte un jet d’hélium II qui peut monter à une trentaine de centimètres de hauteur. Ceci provient du fait que la concentration de l’hélium II en atomes normaux croît lorsque la température s’élève.

Le capillaire ou la poudre d’émeri constitue un obstacle au déplacement pour les atomes normaux, mais pas pour les atomes super fluides, c’est-à-dire en quelque sorte l’analogue d’une membrane hémiperméable, perméable aux atomes fluides et imperméable aux atomes normaux.

L’hélium II se présente alors comme une solution d’atomes normaux dans le solvant que constitue la partie superfluide. Dans la partie chaude, la concentration de cette solution est plus forte et il faut pour que l’équilibre se maintienne avec la parie froide, que la pression dans la partie chaude soit plus forte (analogie avec la pression osmotique mais très lointaine évidemment). D’où un gradient de pression de même sens que le gradient de température et en définitive, l’effet fontaine.

Une théorie correcte montre que l’on doit considérer que le réseau des atomes superfluides à la même entropie qu’au zéro absolu, et possède donc un ordre total, tout au moins le même ordre qu’un cristal parfait au zéro absolu. Ceci vient rejoindre les conclusions tirées de la forme de la courbe de fusion au voisinage du zéro absolu.

Signalons enfin que London et Tisza ont tenté d’interpréter ces curieuses propriétés de l’hélium par les faits que les atomes de \( ^4He\) satisfont à la statistique de Bose-Einstein. Il est de fait que les atomes de \( ^3He\) qui ne satisfont pas à cette statistique ne présentent pas les diverses propriétés spéciales de l’hélium ordinaire, et en particulier ne subissent pas la transition \(\lambda\), ne s’écoulent pas de façon superfluide à travers les capillaires. On a même pu profiter de ce fait pour séparer commodément les deux isotopes.