1. Introduction

Les corps matériels, portés à une température déterminée, émettent de l’énergie sous forme d’un rayonnement électromagnétique qui constitue le rayonnement thermique. Ce rayonnement est formé de la superposition d’une infinité de radiations monochromatiques. Leur répartition dépend du corps émetteur et de la température, mais ne dépend pas du procédé utilisé pour le chauffage. Nous nous bornerons à l’étude du rayonnement thermique proprement dit, en ne considérant pas les phénomènes de luminescence auxquels peuvent donner naissance des procédés d’excitation convenables (décharges électriques par exemple).

Si la température du corps est suffisante, une partie du rayonnement se situe dans le visible. Les radiations rouges apparaissent les premières lorsque la température est progressivement élevée ; à très haute température, des radiations de plus en plus élevées apparaissent dans le spectre du rayonnement émis, l’aspect du corps passant du rouge sombre au rouge blanc, puis au blanc éblouissant.

La photographie infrarouge permet par ailleurs de mettre en évidence l’émission thermique dès la température ordinaire. C’est ce rayonnement purement thermique que nous voulons étudier.

2. Notions élémentaires sur le rayonnement thermique

2.1. Luminance énergétique

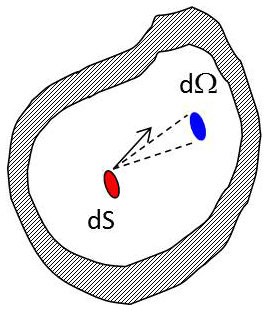
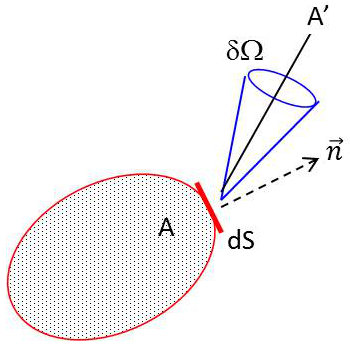Soit un élément de surface \(dS\) entourant un point \(A\) de la surface d’un corps quelconque placé dans le vide et maintenu à une température \(T\). Cet élément émet continuellement de l’énergie dans toutes les directions, sous forme de rayonnement thermique.

Isolons le pinceau de rayon issu de \(dS\) et de directions contenues dans un petit angle solide \(\delta\Omega\) entourant une direction moyenne \(AA'\).

Isolons de plus dans ce pinceau les rayonnements de longueurs d’ondes comprises dans l’intervalle \([\lambda~,~\lambda+d\lambda]\).

Soit \(d^3P_{\lambda}\) la puissance transportée par ces rayonnements (énergie transportée par seconde).

Pour un observateur placé en \(A'\) le rayonnement semble provenir d’un petit élément \(d\sigma\), projection de \(dS\) sur le plan normal à \(AA'\), qui constitue la section droite du pinceau de rayons au niveau de \(dS\).

On a évidemment : \[d\sigma=dS\cos(i)\qquad i=angle(AA',AN)\]

Nous poserons alors : \[d^3P_{\lambda}=B_{\lambda}~d\sigma~d\Omega~d\lambda=B_{\lambda}~\cos(i)~dS~d\Omega~d\lambda\]

Le coefficient \(B_{\lambda}\) qui dépend du corps considéré, du point \(A\) choisi sur le corps, de la température \(T\), de la direction \(AA'\) et de la longueur d’onde \(\lambda\) choisie est appelé luminance énergétique ou pouvoir émissif au point \(A\) dans la direction \(AA'\) et dans la longueur d’onde \(\lambda\).

Considérons maintenant toutes les longueurs d’onde dans le même pinceau de rayons, transportant la puissance totale : \[d^2P=\int d^3P_{\lambda}\]

Nous pouvons écrire : \[d^2P=B~\cos(i)~dS~d\Omega\quad;\quad B=\int B_{\lambda}~d\lambda\]

\(B\) est le pouvoir émissif total du corps considéré au point \(A\), dans la direction \(AA'\) et à la température \(T\).

2.2. Pouvoir absorbant

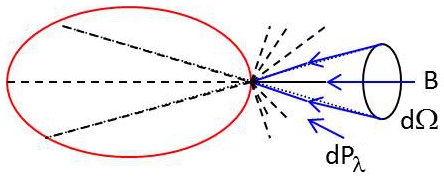Sur la surface \(dS\) du corps, faisons tomber un rayonnement monochromatique de longueur d’onde \(\lambda \), transporté par un faisceau de rayons dont les directions sont contenues dans un petit angle solide \(d\Omega\) entourant la direction moyenne \(BA\).

Soit \(d^2P_{\lambda}\) la puissance transportée par ce rayonnement. L’élément de surface \(dS\) en réfléchit ou en diffuse une partie. Une autre partie de ce rayonnement peut être transmise par le corps, c’est-à-dire ressortir de l’autre côté après avoir pénétré suivant \(dS\).

Soit alors \(a_{\lambda}~d^2P_{\lambda}\) la fraction de puissance reçue par \(dS\) qui n’est ni réfléchie, ni diffusée, ni transmise et se trouve absorbée par le corps. Le coefficient \(a_{\lambda}\) est le facteur d’absorption ou pouvoir absorbant du corps au point \(A\) dans la direction \(BA\) et pour la longueur d’onde.

Corps noir

Nous désignons sous le nom de corps noir un corps qui, en tout point, pour des rayonnements de direction et de longueur d’onde quelconques, présente un facteur d’absorption égal à l’unité. Un tel corps, lorsqu’il est maintenu à la température ordinaire et éclairé par une source lumineuse, ne renvoie aucun des rayons lumineux qu’il reçoit et apparaît parfaitement noir, d’où sa dénomination.

Un corps noir par contre émet comme les autres un rayonnement thermique qui devient visible si la température du corps noir est assez élevée ; nous verrons même qu’il est, à température égale, plus brillant que les autres.

2.3. Aspect corpusculaire du rayonnement

Le rayonnement de fréquence est apporté par les photons (corpuscules de rayonnement), chacun d’entre eux contribuant à une énergie : \[E=h~\nu\qquad h=6,62\times 10^{-34}~joules\]

Le photon est également porteur de la quantité de mouvement : \[p=\frac{h~\nu}{c}\]

2.4. Pression de radiation

Le rayonnement lumineux est de nature électromagnétique : le long d’un rayon lumineux se propagent un champ électrique et une excitation magnétique perpendiculaires. Lorsqu’un rayonnement lumineux tombe sur une surface métallique par exemple, il y induit des courants alternatifs de fréquence \(\nu\) égale à sa propre fréquence.

L’action de l’induction magnétique sur ces courants induits fait apparaître une force de répulsion exercée par le rayonnement sur cette surface. Cette force est à l’origine de la pression de radiation. Nous calculerons cette pression de radiation en nous reportant à l’aspect corpusculaire du rayonnement.

Considérons un rayonnement monochromatique de fréquence \(\nu\) tombant sous l’incidence \((i)\) sur une surface (unitaire). Soit \(n\) le nombre de photons par unité de volume contenus dans le faisceau incident.

Ces photons ont, suivant la normale à la surface, une composante de quantité de mouvement égale à : \[\frac{h~\nu~\cos(i)}{c}\]

La réflexion change le signe de cette composante dont la variation totale, pour chaque photon incident, est par suite  : \[\frac{2~h~\nu~\cos(i)}{c}\]

Un calcul tout à fait analogue à celui de la pression d’un gaz parfait montre alors que le nombre de photons tombant par seconde sur la surface unité est \(n~c~\cos(i)\) (c étant la vitesse de translation des photons), soit une variation totale de quantité de mouvement égale à la pression de radiation : \[P_r=2~n~h~\nu~\cos^2(i)=u~\cos^2(i)\]

• \(2~n\) est le nombre de photons par unité de volume au dessus de la surface réfléchissante (faisceau incident + faisceau réfléchi) ;

• \(u\) représente la densité d’énergie au-dessus de la paroi.

La pression de radiation ne doit pas être confondue avec la pression radiométrique qui apparaît lorsqu’une surface, placée dans une enceinte imparfaitement vidée, est éclairée sur une de ses faces. Cette face est alors portée à température plus élevée que la face opposée ; elle renvoie plus vite les molécules gazeuses qui viennent la frapper, d’où un effet de recul et la pression radiométrique.

Cette dernière est plus importante que la pression de radiation si le vide est imparfait, mais elle disparaît lorsque l’enceinte est correctement vidée et seule subsiste la pression de radiation, mesurable par une méthode de torsion.

2.5. Effet Doppler

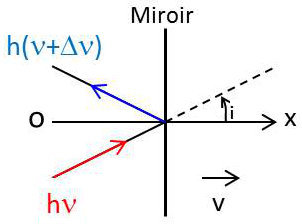Supposons qu’un observateur fasse tomber sur un miroir plan perpendiculaire à \(Ox\) un faisceau lumineux parallèle, monochromatique de fréquence \(\nu\), sous l’angle d’incidence \(i\).

Si le miroir est immobile par rapport à l’observateur, celui-ci peut vérifier, par une méthode spectrographique, que le faisceau réfléchi à la même fréquence \(\nu\).

Si par contre le miroir se déplace le long de \(Ox\) avec la vitesse \(v\) par rapport à l’observateur, le spectrographe indique que le faisceau est réfléchi avec une fréquence : \[\nu'=\nu~\Big\{1-2~\frac{v}{c}~\cos(i)\Big\}\]

Cette relation peut être établie à partir de considérations ondulatoires classiques. Nous allons la retrouver à partir de l’aspect corpusculaire du rayonnement.

Les photons de fréquence \(\nu\) exercent sur l’unité de surface du miroir une force de poussée égale à la pression de radiation. Désignons par \(n_c\) le nombre de photons par seconde. La pression de radiation est : \[p=n_c~\frac{2~h~\nu}{c}~\cos(i)\]

Pendant une seconde, le miroir s’est déplacé de \(v\) et l’unité de surface a reçu de ces photons un travail : \[W=p~\nu=n_c~\frac{2~h~\nu}{c}~\nu~\cos(i)\]

Ceux-ci ont donc perdu une énergie : \[\Delta(n_c~h~\nu)=n_c~h~\Delta\nu=W=n_c~\frac{2~h~\nu}{c}~\nu~\cos(i)\]

La fréquence s’est donc abaissée de : \[\Delta\nu=\nu~\frac{2~\nu}{c}~\cos(i)\]

Elle est donc passée à la valeur : \[\nu'=\nu~\Big\{1-\frac{2~\nu}{c}~\cos(i)\Big\}\]

2.6. Rayonnement en équilibre dans le vide

Nous considérons une enceinte fermée parfaitement vidée à parois imperméables à tout rayonnement, maintenue à la température fixe \(T\). Ses parois internes émettent constamment du rayonnement thermique ; par ailleurs, chaque portion de paroi absorbe, diffuse ou réfléchit les rayonnements émis par les autres portions de paroi.

La température étant maintenue constante, un équilibre de régime s’établit et le rayonnement qui emplit l’enceinte atteint une répartition permanente. Nous admettrons, ce qui est naturel du fait que l’enceinte est parfaitement déterminée, que cette répartition d’équilibre ne dépend que de la température \(T\) et qu’elle est unique pour chaque température.

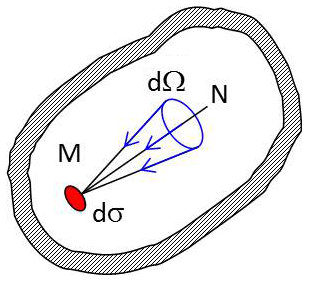Considérons alors un petit élément de surface \(d\sigma\) entourant un point \(M\) à l’intérieur de l’enceinte ; soit \(MN\) la normale à cet élément de surface \(d\sigma\). Celui-ci est traversé par un rayonnement thermique.

Isolons dans ce rayonnement celui qui est transporté par des rayons de direction comprise dans un petit angle solide \(d\Omega\) entourant la direction \(MN\) et dont la longueur d’onde appartient à l’intervalle \([\lambda,~\lambda+d\lambda]\).

La puissance \(d^3P_{\lambda}\) transportée par ces rayonnements peut être écrite sous la forme : \[d^3P_{\lambda}=E_{\lambda}~d\sigma~d\Omega~d\lambda\]

Le coefficient \(E_{\lambda}\) dépend de la température et de la longueur d’onde choisie. Il pourrait sembler à priori qu’il dépende également de la forme et de la nature de l’enceinte, de la position du point \(M\) dans l’enceinte et de l’orientation de \(d\sigma\). Il n’en est rien (la démonstration est possible) et le rayonnement dans l’enceinte a une répartition homogène et isotrope, indépendante de la nature et de la forme de l’enceinte.

Le coefficient \(E_{\lambda}\) est désigné sous le nom d’intensité spécifique du rayonnement thermique dans le vide, à la température \(T\) et pour la longueur d’onde \(\lambda\). Et nous énonçons le résultat suivant :

L’intensité spécifique du rayonnement thermique dans le vide ne dépend que de la température \(T\) de l’enceinte qui renferme le rayonnement et de la longueur d’onde choisie. Elle est indépendante de la nature et de la forme de l’enceinte et pour toutes les directions de rayonnement.

On a donc: \(E_{\lambda}=f(\lambda,~T)\).

Intégrant sur l’ensemble des longueurs d’onde, nous obtenons la puissance totale transportée par les rayonnements du faisceau \([d\sigma,d\Omega]\) : \[d^2P=d\sigma~d\Omega\int_0^{\infty} E_{\lambda}~d\lambda=E~d\sigma~d\Omega\]

Le coefficient \(E\) est désigné sous le nom d’intensité spécifique totale du rayonnement thermique dans le vide à la température \(T\). Ce coefficient \(E\) est indépendante de l’enceinte et ne dépend que de la température \(T\).

2.7. Densité d’énergie rayonnante

La répartition du rayonnement étant homogène et isotrope, chaque élément \(dv\) de l’enceinte renferme une énergie rayonnante \(u~dv\) transportée par des rayonnements dont l’intensité est répartie dans toutes les directions avec une symétrie sphérique, \(u\) représentant la densité d’énergie rayonnante, valeur qui est la même en tout point de l’enceinte et ne dépend que de la température.

Si nous trions parmi ces rayonnements ceux dont la longueur d’onde appartient à l’intervalle \([\lambda,~\lambda+d\lambda]\), leur énergie par unité de volume est \(u_{\lambda}~d\lambda\). Elle est la même en tout point de l’enceinte et ne dépend que de \(T\) et de \(\lambda\).

Isolons en outre les rayonnements dont la direction de propagation est comprise dans un petit angle solide \(d\Omega\) entourant la direction \(MN\). Leur énergie par unité de volume est : \[\frac{d\Omega}{4~\pi}~u_{\lambda}~d\lambda\]

Une surface \(d\sigma\) perpendiculaire à \(MN\) reçoit par seconde de la part de ces rayonnements toute l’énergie qui leur correspond dans un cylindre de base \(d\sigma\) et de hauteur \(c\), soit : \[\frac{c}{4~\pi}~d\sigma~d\Omega~u_{\lambda}~d\lambda\]

Cette énergie est égale, par définition, à \(E_{\lambda}~d\sigma~d\Omega~d\lambda\).

On en tire : \[E_{\lambda}=\frac{c}{4~\pi}~u_{\lambda}\qquad\text{et, par intégration~:}\quad E=\frac{c}{4~\pi}~u\]

2.8. Pression de radiation exercée par le rayonnement thermique en équilibre

Chaque radiation monochromatique est transportée par un ensemble de rayonnements présentant une symétrie. L’effort tangentiel exercé sur les parois de l’enceinte est alors nul. Pour obtenir la pression normale, on remarque que chaque radiation monochromatique atteint la paroi sous tous les angles d’incidence \((i)\) uniformément répartie sur \([0,~\pi/2]\).

La pression exercée par les rayonnements de longueur d’onde appartenant à \([\lambda,~\lambda+d\lambda]\) est donc : \[dP_n(\lambda)=u_{\lambda}~d\lambda~\cos^2(i)=\frac{u_{\lambda}~d\lambda}{3}\]

D’où la pression totale : \[P_n=\frac{u}{3}\]

Le rayonnement thermique en équilibre dans le vide exerce donc sur les parois de l’enceinte qui le renferme une pression uniforme, égale au tiers de sa densité d’énergie rayonnante. Cette propriété va constituer la clef des applications de la thermodynamique classique à l’étude du rayonnement thermique.

Le rayonnement dans l’enceinte présente en effet beaucoup d’analogies avec un système thermodynamique tel qu’une masse gazeuse. Cependant, la pression qu’il exerce sur les parois de l’enceinte ne dépend que de la température.

Elle est indépendante du volume de l’enceinte et ne varie pas si ce volume est modifié de manière isotherme : cela résulte du fait que le nombre total des photons situés dans l’enceinte n’est nullement imposé, comme ce serait le cas pour les molécules d’un gaz. Les parois de l’enceinte, lors d’une expansion isotherme, émettent constamment de nouveaux photons, de façon à maintenir constante la densité de leur répartition.

2.9. Pouvoir émissif et pouvoir absorbant

Dans une enceinte parfaitement vidée maintenue à une température \(T\), nous plaçons un corps quelconque. Lorsque l’équilibre à la température \(T\) est réalisé, le corps absorbe à chaque instant autant d’énergie qu’il en émet puisque son énergie interne reste constante. La puissance totale absorbée est égale à la puissance totale émise.

Or, un élément \(dS\) du corps reçoit, des rayonnements de longueur d’onde comprises dans la bande \([\lambda,~\lambda+d\lambda]\) et de directions comprises dans un angle solide \(d\Omega\), une puissance \(E_{\lambda}~d\lambda~\cos(i)~dS~d\Omega\) et absorbe une fraction \(a_\lambda\) de cette puissance.

La puissance totale absorbée obtenue en intégrant sur toutes les longueurs d’onde, toutes les directions de rayonnement et tous les éléments \(dS\) est donc : \[P_{\text{absorbée}}=\iiint a_k~E_{\lambda}~\cos(i)~dS~d\lambda~d\Omega\]

Nous obtiendrons de même pour la puissance émise : \[P_{\text{émise}}=\iiint B_{\lambda}~\cos(i)~dS~d\lambda~d\Omega\]

Le fait que l’énergie interne est constante exige que : \[\iiint (a_k~E_{\lambda}-B_{\lambda})~\cos(i)~dS~d\lambda~d\Omega=0\]

Le corps est de forme et de nature quelconques ; les variations de \(E_{\lambda}\) ou \(a_{\lambda}\) avec la longueur d’onde sont absolument quelconques. On ne pourra donc être assuré que l’intégrale est nulle dans tous les cas que si l’élément différentiel lui-même est constamment nul, soit : \[\frac{B_{\lambda}}{a_{\lambda}}=E_{\lambda}\]

Ce rapport est indépendant de la direction choisie et ne dépend que de la longueur d’onde considérée et de la température du corps ; il est égal à l’intensité spécifique du rayonnement thermique dans le vide pour cette longueur d’onde, à la température du corps.

Nous en déduisons immédiatement que, pour le corps noir, \(a_{\lambda=1}\) pour toutes les longueurs d’onde. Par suite et pour le corps noir : \(B_{\lambda}=E_{\lambda}\). Pour tous les autres corps, par contre, on aura \(B_{\lambda}<E_{\lambda}\), car \(a_{\lambda}<1\) par définition.

Le corps noir est donc celui qui émet le plus d’énergie par rayonnement thermique à température donnée. C’est celui qui paraît le plus brillant à température élevée.

Remarque

La puissance rayonnée par l’élément \(dS\) d’un corps noir dans un angle solide \(d\Omega\) entourant une direction faisant un angle \((i)\) avec la normale à \(dS\) est :

\[\begin{aligned} dP&=B~dS~\cos(i)~d\Omega=E~dS~\cos(i)~d\Omega\\ B&=\int_0^{\infty} B_{\lambda}~d\lambda=\int\_0^{\infty} E_{\lambda}~d\lambda=E\qquad\text{qui ne dépend que de T.}\end{aligned}\]

Chaque élément de surface émet donc une intensité proportionnelle au cosinus de l’angle d’émission ; l’émission thermique du corps noir suit donc une loi de Lambert. Le flux rayonné dans tout l’espace par une surface du corps noir égale à l’unité est donc : \[R=\pi~B=\pi~E\]

\(R\) est la radiance énergétique du corps noir, elle ne dépend que de la température \(T\).

2.10. Réalisation pratique du corps noir

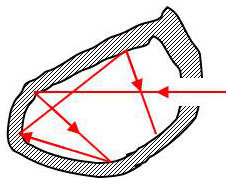Perçons dans une enceinte maintenue à la température \(T\) un trou de diamètre très petit devant le diamètre de l’enceinte. Ce trou peut être considéré comme une portion de surface dont l’émission est celle du corps noir.

Ceci peut être prouvé de deux façons :

1. Viser l’intérieur de l’enceinte à travers le trou revient à viser directement le rayonnement thermique en équilibre à l’intérieur de l’enceinte. On en déduit immédiatement que la luminance \(B_{\lambda}\) du trou pour toutes les longueurs d’onde et dans chaque direction est \(E_{\lambda}\) (c’est-à-dire celle du corps noir)

2. On peut aussi considérer que le trou constitue une portion de surface parfaitement absorbante pour toutes les radiations. Un rayonnement quelconque tombant sur le trou entre en effet dans l’enceinte et ne peut retrouver la sortie qu’après une infinité de réflexions. Il est un peu absorbé à chacune d’elles et aucun rayonnement ne ressort du trou qui constitue donc une portion de surface parfaitement absorbante pour toutes les radiations.

3. Étude thermique du rayonnement

3.1. Compression isotherme du rayonnement. Loi de Stefan

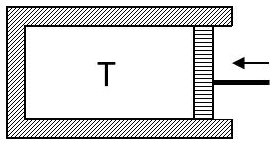Un corps de pompe diatherme, parfaitement vidé, dont les parois sont un peu absorbantes par toutes les longueurs d’onde, est maintenue à une température constante \(T\). Le rayonnement qu’il contient est le rayonnement d’équilibre à la température \(T\).

Repoussons lentement le piston vers la gauche ; nous réalisons ainsi une compression isotherme du rayonnement au cours de laquelle l’énergie totale du rayonnement contenu dans l’enceinte varie d’une quantité \(\Delta U=-u\) Cette formule s’explique par le fait que le volume a varié d’une quantité égale à l’unité, que \(T\) n’a pas varié et que la densité d’énergie rayonnante \(u\) ne dépend que de \(T\).

Cette opération est une opération réversible au cours de laquelle la fonction de Helmholtz \((U-T~S)\) du système thermodynamique formé par le rayonnement en équilibre a varié de : \[\Delta(U-T~S)=W=-P_n~\Delta V=-P_n=+\frac{u}{3}\]

Appliquons la première relation d’Helmoltz : \[\Delta U=\Delta F-T~\frac{\partial}{\partial T}~(\Delta F)\]

La dérivée partielle est prise à volume initial et à volume final constants. Nous obtenons donc : \[-u=\frac{u}{3}-\frac{T}{3}~\frac{du}{dT}\qquad\text{u ne dépend que de T.}\]

En définitive, par intégration : \[\frac{1}{4}~\frac{du}{u}=\frac{dT}{T}\quad\Rightarrow\quad u=K~T^4\]

C’est la loi de Stefan. La densité d’énergie rayonnante varie donc proportionnellement à la puissance 4 de la température thermodynamique.

Nous en déduisons que l’intensité spécifique du rayonnement thermique dans le vide et la radiance du corps noir varient elles aussi comme la puissance 4 de la température thermodynamique. En effet :

\[\begin{aligned} &E=\frac{c}{4~\pi}~u=\frac{K~c}{4~\pi}~T^4\\ &R=\pi~E=\frac{K~c}{4}~T^4=\sigma~T^4\end{aligned}\]

La thermodynamique classique nous apprend seulement que le coefficient \(\sigma\) est constant, mais elle ne nous donne pas sa valeur. Les mesures confirment la loi en \(T^4\) et donne pour ce coefficient la valeur : \[\sigma\approxeq 5,7\times 10^{-6}~W~m^{-2} K^{-4}\]

Le corps noir à 3000 K a donc une radiance d’environ 4 600 kW/m².

Pour le soleil, la radiance est d’environ 80 000 kW/m², ce qui indique (si on l’assimile à un corps noir) une température superficielle d’environ 5950 K.

3.2. Répartition spectrale du corps noir. Lois de Wien

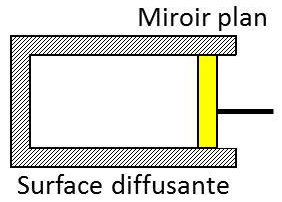Enfermons maintenant le rayonnement dans une enceinte aux parois parfaitement non absorbantes, c’est-à-dire que \(a_k=0\). Dans ce but, nous le plaçons dans un corps de pompe à parois parfaitement diffusantes, fermé par un piston parfaitement réfléchissant.

Nous sommes ainsi assurés qu’aucun échange d’énergie n’est possible entre le rayonnement et les parois, si ce n’est sous forme de travail exercé par le piston contre la pression de radiation.

Un déplacement du piston vers la gauche permet donc de réaliser une compression adiabatique du rayonnement. De plus, la nature parfaitement diffusante des parois nous permet d’affirmer que le rayonnement présent dans le corps de pompe aura toujours la symétrie sphérique et que, par suite, la pression exercée par le rayonnement sur le piston sera toujours liée à la densité d’énergie rayonnante dans le corps de pompe par la relation \(P=u/3\), ceci quelle que soit la répartition en longueur d’onde du rayonnement présent dans l’enceinte.

On peut ainsi démontrer que, si le rayonnement présent dans l’enceinte est initialement le rayonnement d’équilibre à une certaine température \(T\), toute compression adiabatique réversible va nous conduire à un rayonnement dont la répartition en longueur d’onde sera celle qui correspond à l’équilibre à une autre température \(T'\). Ce résultat sera ici admis.

Nous pouvons alors calculer, en appliquant la loi de Stefan, la variation de température \(dT\) qui accompagne une variation adiabatique \(dV\) du volume de l’enceinte. Nous écrivons pour cela que la variation totale d’énergie interne du rayonnement est égale au travail qu’il a reçu :

\[\begin{aligned} &dU=d(u~V)=u~dV+V~du=dW=-\frac{u}{3}\\ \text{c'est-à-dire :}\quad &\frac{du}{u}+\frac{4}{3}~\frac{dV}{V}=0\end{aligned}\]

Par ailleurs : \[\frac{du}{u}=4~\frac{dT}{T}\]

Il vient donc : \[\frac{dT}{T}=-\frac{1}{3}~\frac{dV}{V}\quad\Rightarrow\quad T^3~V=cte\]

Nous allons montrer à présent que chacune des radiations comprises dans l’enceinte a subi une variation relative de longueur d’onde égale à \((-dT/T)\). La démonstration peut être faite par une étude purement ondulatoire du rayonnement. Elle peut être plus rapide en passant à la nature corpusculaire du rayonnement.

Les parois et le piston étant parfaitement non absorbants, le nombre de photons présents dans l’enceinte reste constant, mais leur longueur d’onde varie lors de leurs réflexions successives sur le piston mobile. Soit \(v\) la vitesse de translation infiniment petite du piston et \(S\) sa surface. La variation de volume de l’enceinte pendant le temps \(dt\) est \(dV=-S~v~dt\).

Pendant le temps \(dt\), chaque photon a frappé une infinité de fois le piston et il l’a frappé sous toutes les incidences possibles puisque les parois parfaitement diffusantes imposent pour chacun des photons un ensemble de trajectoires réparties suivant la symétrie sphérique.

Considérons alors les photons dont la longueur d’onde est située dans la bande \(\lambda,~\lambda+d\lambda\). L’ensemble de ces photons dont l’énergie totale est \(v~u_{\lambda}~d\lambda\) exerce sur le piston une force : \[dF=\frac{ u_{\lambda}~d\lambda~S}{3}\]

Le travail pendant le temps dt vaut : \[dW=\frac{-u_{\lambda}~d\lambda~S~v~dt}{3}=\frac{u_{\lambda}~d\lambda~dV}{3}\]

Ces photons, en nombre constant, subissent une variation relative de fréquence égale à leur variation relative d’énergie, soit : \[\frac{d\nu}{\nu}=-\frac{1}{V}~\frac{dW}{u_{\lambda}~d\lambda}=-\frac{1}{3}~\frac{dV}{V}\]

Chacun des photons présents dans l’enceinte subit donc une variation relative de longueur d’onde : \[\frac{d\lambda}{\lambda}=-\frac{d\nu}{\nu}=-\frac{1}{3}~\frac{dV}{V}=-\frac{dT}{T}\]

Ce qu’il fallait démontrer.

3.2.1. Lois de déplacement de Wien

Nous énonçons ces lois sans démonstration :

– Première loi de Wien : Lorsque par compression adiabatique, la température d’équilibre du rayonnement passe de \(T\) à \(T'\), la longueur d’onde de chacune des radiations contenues dans l’enceinte varie dans le rapport \(T/T'\).

Aux radiations dont la longueur d’onde était initialement \(\lambda\) correspondent en fin de compression des radiations de longueur d’onde : \[\lambda'=\frac{T}{T'}~\lambda\qquad \frac{T}{T'}<1~~\text{en compression adiabatique}\]

– Deuxième loi de Wien : La densité d’énergie est \((T'/T)^5\) fois plus grande.

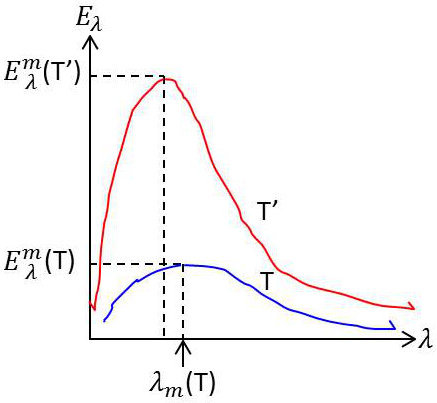Les lois de déplacement de Wien permettent de prévoir la forme de la loi de variation de la densité d’énergie \(E_\lambda\) en fonction de la longueur d’onde pour une température donnée \(T\).

Sur le diagramme \(E_{\lambda}\) (qui est proportionnel à \(u_{\lambda}\)), on voit apparaître un maximum \(E_{\lambda}^m\) pour une longueur d’onde \(\lambda_m\).

Nous passons alors de la courbe de répartition spectrale à une autre température \(T'\) en multipliant les abscisses \(\lambda\) par \((T/T')\) et les ordonnées \(E_{\lambda}\) par \((T'/T)^5\), soit au moyen de deux affinités successives. Au maximum de la courbe initiale va correspondre le maximum de la courbe transformée.

Remarque

Si nous modifions simultanément \(\lambda\) et \(T\) de façon que \(\lambda~T\) reste constante, \(E_{\lambda}\) varie comme \(T^5\), ce qui veut dire que le rapport \(E_{\lambda}/T^5\) reste constant tant que \(T\) reste constant ; il n’est donc fonction que du produit \(\lambda~T\) et nous pouvons écrire : \[E_{\lambda}=T^5~f(\lambda~T)\]

Ou bien, après avoir posé : \((\lambda~T)^5~f\lambda~T)=\varphi(\lambda~T)\) : \[E_{\lambda}=\lambda^{-5}~\varphi(\lambda~T)\]

C’est là tout ce que la thermodynamique classique nous permet d’apprendre sur la répartition spectrale du rayonnement. Pour aller plus loin et découvrir la forme de la fonction \(\varphi(\lambda~T)\), il faut passer à l’étude statistique du rayonnement thermique dans le vide, rayonnement que nous considérerons comme une assemblée de photons qui obéissent à la statistique de Bose-Einstein.

4. Rayonnement en équilibre dans une enceinte thermique

4.1. Étude statistique

Nous considérons une enceinte cubique de côté \(a\), vide de tout gaz, maintenue à la température \(T\). Cette enceinte est remplie de photons de fréquences diverses qui se propagent à l’intérieur à la vitesse \(c\) et se réfléchissent sur les parois. Nous sommes ainsi en présence d’une assemblée de photons dont nous allons chercher la répartition suivant les fréquences \(\nu_i\) ou, ce qui revient au même, suivant les niveaux d’énergie \(h~\nu_i\).

Il nous faut pour cela chercher tout d’abord l’ordre de dégénérescence \(g_i\) du niveau d’énergie \(h~\nu_i\), c’est-à-dire le nombre de rayonnements physiquement distincts qui peuvent se propager dans l’enceinte avec la fréquence \(\nu_i\). Nous savons par ailleurs que les photons satisfont à la statistique de Bose-Einstein.

Nous avons déjà traité le problème consistant à chercher la répartition d’équilibre d’une telle assemblée dans le cas où le nombre total de systèmes constituant l’assemblée est déterminé. Ici, le nombre de photons contenus dans l’enceinte n’est pas imposé, des photons pouvant être émis par les parois de l’enceinte.

La condition \(\sum n_i=cte\) ou encore \(\sum \delta n_i=0\) disparaît par conséquent et avec elle disparaît le multiplicateur de Lagrange \(\alpha\). Seule subsiste la condition : \[\sum_i U_i~\delta n_i=0\qquad\text{ici :}\quad U_i=h~\nu_i\]

La répartition d’équilibre à la température \(T\) est donc donnée par : \[n_i=\frac{g_i}{\exp(h~\nu_i/k~T)-1}\]

Nous grouperons dans un même niveau d’énergie tous les photons de fréquence \(\nu_i\) telle que \(\nu<\nu_i<\nu+d\nu\) et nous désignons par \(g(\nu)~d\nu\) la dégénérescence de ce niveau, c’est-à-dire le nombre de rayonnements distincts qui peuvent se propager dans l’enceinte et dont la fréquence est contenue dans l’intervalle \([\nu,~\nu+d\nu]\).

Le nombre de photons de fréquence de cet intervalle que contient l’enceinte lorsque l’équilibre à la température \(T\) est réalisé dès lors que : \[dn=\frac{g(\nu)~d\nu}{\exp(h~\nu_i/k~T)-1}\]

Cherchons à calculer \(g(\nu)~d\nu\). Nous porterons pour cela notre attention sur la nature ondulatoire du rayonnement et considérons que seuls peuvent se maintenir en équilibre dans l’enceinte les rayonnements qui y forment un système d’ondes stationnaires, c’est-à-dire qui correspondent à des ondes électromagnétiques en résonance dans l’enceinte.

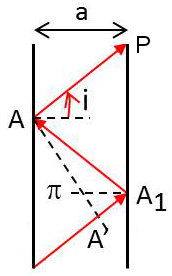Considérons alors deux plans réfléchissants parallèles situés à la distance \(a\) et une onde de fréquence \(\nu\) se propageant entre eux suivant la direction \(AP\) qui fait l’angle \(i\) avec la normale commune aux deux plans.

Cette onde se réfléchit sur les deux plans et donne donc naissance entre eux à des ondes se propageant suivant les directions \(AP\) et \(A_1A\). Soit \(AA'\) la trace d’un plan d’onde \(\pi\) (perpendiculaire au plan de la figure).

En \(P\) arrive une vibration de phase \(\phi_1\) qui provient directement du point \(A\) suivant le rayon \(AP\) ; la phase de cette vibration est donc : \[\phi_P=\phi_A-\frac{2~\pi}{\lambda}~AP\]

\(\lambda\) : longueur d’onde dans le vide.

Or, en \(P\) arrive aussi une vibration provenant du point \(A'\) suivant le chemin \(A'A_1AP\) et de phase : \[\phi'_P=\phi'_A-\frac{2~\pi}{\lambda}~(A'A_1+A_1A+AP)\]

Il y aura interférence constructive entre ces deux vibrations si leur différence de phase est un multiple entier de \(2~\pi\), c’est-à-dire, puisque \(\phi_{A'}=\phi_A\), si le chemin \(A'A_1A\) contient un nombre entier de longueurs d’onde, soit, \(K\) étant entier : \[A'A_1+A_1A=K~\lambda\]

Or : \[A_1A=\frac{a}{\cos(i)}\quad;\quad A'A_1=A_1A~\cos(i)\]

On aura donc à la résonance : \[2~a~\cos(i)=K~\lambda\]

À l’intérieur de l’enceinte cubique, la condition de résonance doit être satisfaite pour les trois paires de faces réfléchissantes en regard, soit, en rapportant la direction du rayonnement au trièdre trirectangle formé par les arêtes de l’enceinte cubique et en désignant par \((\alpha,\beta,\gamma)\) les cosinus directeurs de la direction du rayonnement de fréquence \(\nu\) et de longueur d’onde \(\lambda=c/\nu\) : \[\lambda=2~a\quad;\quad\frac{\alpha}{p}=2~a\quad;\quad\frac{\beta}{q}=2a\quad;\quad\frac{\gamma}{r}=2~a \qquad p,~q,~r\text{ entiers}\]

En raison de la relation aux cosinus directeurs : \[\alpha^2+\beta^2+\gamma^2=1 \quad\Rightarrow\quad p^2+q^2+r^2=\frac{4~a^2}{\lambda^2}=\frac{4~a^2~\nu^2}{c^2}\]

Un rayonnement de longueur d’onde \(\lambda\) ne peut se trouver en résonance dans l’enceinte que s’il existe un groupe de trois nombres entiers \(p, q, r\) vérifiant cette relation. Il est évident que si \(\lambda\) est rigoureusement déterminée, un tel groupe de nombres n’existe pas, la probabilité de trouver un point à coordonnées entières sur la sphère de rayon \(2~a/\lambda\) étant nulle.

Cherchons à présent le nombre de tels rayonnements dont la fréquence est comprise dans l’intervalle \(\lambda,~\lambda+d\lambda\). Cela revient à trouver le nombre de points à coordonnées entières et positives \(p,~q,~r\) compris entre les sphères de rayons : \[r=2~a~\frac{\nu}{c}\qquad\text{et}\qquad r+dr=2~a~\frac{\nu+d\nu}{c}\]

Ce nombre est égal au volume compris entre l’octet (puisque nous nous limitons aux coordonnées positives) de rayon \(r\) et \(r + dr\). C’est-à-dire : \[dn=d\Big(\frac{4}{3}~\pi~r^3\Big)=d\Big(\frac{4}{3}~\pi~\frac{a^3}{c^3}~\nu^3\Big)=4~\pi~\frac{V}{c^3}~\nu^2~d\nu\]

À chaque direction de rayonnement peuvent en outre correspondre deux rayonnements distincts polarisés à angle droit, soit en définitive un nombre de rayonnements physiquement discernables de fréquences contenues dans \([\lambda,~\lambda+d\lambda]\) dans l’enceinte de volume \(V\). \[g(\nu)~d\nu=\frac{8~\pi~V}{c^3}~\nu^2~d\nu\]

Ce qui nous conduit à un nombre de photons de fréquences contenues dans \([\lambda,~\lambda+d\lambda]\) à la température \(T\) : \[dn=\frac{1}{\exp(h~\nu/k~)-1}~\frac{8~\pi~V}{c^3}~\nu^2~d\nu\]

On montre que ce résultat est valable quelque soit la nature et la forme de l’enceinte qui contient donc, à la température \(T\) par unité de volume, un nombre de photons de fréquences contenus dans l’intervalle \([\lambda,~\lambda+d\lambda]\) : \[dn=n(\nu)~d\nu=\frac{1}{\exp(h~\nu/k~T)-1}~\frac{8~\pi~V}{c^3}~\nu^2~d\nu\]

C’est-à-dire une densité d’énergie rayonnante dans la bande de fréquences \([\lambda,~\lambda+d\lambda]\) \[u_{\nu}~d\nu=\frac{1}{\exp(h~\nu/k~T)-1}\frac{8~\pi~V}{c^3}~\nu^2~d\nu\]

Si l’on repère les rayonnements par leur longueur d’onde \(\nu=c/\lambda\), alors \(|d\nu|=c~|d\lambda|/\lambda^2\) et en posant \(u_{\nu}~d\nu=u_{\lambda}~d\lambda\), on obtient,tous calculs faits : \[u_{\lambda}=\frac{8~\pi~h~c~\lambda^{-5}}{\exp(h~c/k~T)-1}\]

Les points \(p,~q,~r\) sont uniformément répartis dans le volume séparant les deux octets considérés. Il en résulte que les rayonnements correspondant à chaque intervalle de fréquence sont uniformément répartis suivant toutes les directions dans l’enceinte. Nous retrouvons ainsi l’isotropie de la distribution spatiale du rayonnement thermique.

4.2. Formule de Planck

De la valeur obtenue pour la densité d’énergie rayonnante \(u_\lambda\), nous tirons comme précédemment l’intensité du rayonnement thermique dans le vide à la température \(T\) et pour la longueur d’onde \(\lambda\), soit :

\[\begin{aligned} E_{\lambda}&=\frac{c}{4~\pi}~u_{\lambda}=\frac{C_1~\lambda^{-5}}{\exp(C_2/\lambda~T)-1}\\ C_1&=2~h~c^2\qquad;\qquad C_2=\frac{h~c}{k}\end{aligned}\]

Nous retrouvons ainsi la forme que nous avions prévue pour la loi de variation de \(E_{\lambda}\) avec la longueur d’onde, avec ce résultat complémentaire que la fonction \(\varphi(\lambda,~T)\) se trouve maintenant parfaitement déterminée, alors que la thermodynamique classique était impuissante à nous renseigner à ce sujet.

Il est évident que les lois de Wien et de Stefan se déduisent immédiatement de la formule de Planck.

Il est notamment possible de calculer à la température \(T\) la valeur de l’intensité spécifique totale du rayonnement : \[E=\int_0^{\infty} E_{\lambda}~d\lambda\]

et d’en déduire la radiance \(R\) du corps noir ainsi que, par suite, la constante de Stefan \(\sigma\) que la thermodynamique laissait indéterminée.

Le calcul conduit à : \[\sigma=\frac{2~\pi^5~k^4}{15~c^2~h^3}=5,672\times 10^{-8}~W~m^{-2}~K^{-4}\]

en bon accord avec les résultats expérimentaux.

Application de la formule de Planck

La formule de Planck indique que la luminance spectrale énergétique du corps noir s’exprime en fonction de la température thermodynamique par la relation : \[B_{\lambda}=\frac{2~h~c^2~\lambda^{-5}}{\exp(h~c/k~\lambda~T)-1}\]

Il est donc possible de mesurer directement la température d’un corps noir dans l’échelle thermodynamique en mesurant la luminance de ce corps dans une longueur d’onde déterminée quelconque.

C’est ainsi que la température de l’intérieur d’un four s’obtient directement par une visée de l’ouverture du four (nous savons qu’un petit trou percé dans l’enceinte se comporte comme un corps noir) au moyen d’un pyromètre optique.

Cet appareil comporte un filtre qui isole une bande spectrale du rayonnement émis (un simple verre rouge dans les appareils industriels). On mesure la luminance de l’image fournie par l’objectif de la lunette égale à celle de l’objet aux pertes par réflexion et absorption près) en lui superposant un filament dont on règle le chauffage jusqu’à ce qu’il disparaisse dans le fond de l’image.

L’emploi d’un appareil soigné, muni d’un filtre isolant un intervalle de longueur d’onde bien délimité, permet de rendre la mesure assez précise pour que le pyromètre optique puisse être considéré comme définissant directement l’échelle thermodynamique de températures ; c’est lui qui sert de base à l’échelle internationale dans le domaine des températures supérieures à la température de fusion de l’or.