1. Introduction

Ce qui importe avant tout pour l’utilisateur d’un système de transmission, c’est la qualité du message reçu. Celui-ci devra être une réplique aussi semblable que possible du message émis.

Or, le processus de transmission conduit inévitablement à une dégradation du message dont la cause incontournable est le bruit que l’on rencontre dans tous les équipements électroniques. Celui-ci va se superposer au signal reçu et perturber l’intelligibilité du message.

Chaque modulateur présente un comportement différent vis-à-vis du bruit. Il convient d’examiner les effets du bruit sur la qualité de la transmission, en fonction des différentes techniques de modulation, pour aboutir à une esquisse de comparaison.

2. Mesure quantitative de la qualité d’une transmission

Le signal de sortie du récepteur peut s’écrire, \(m(t)\) étant le signal de modulation initial : \[y(t)=k~m(t)+\text{termes de bruit}\]

La qualité de la transmission sera d’autant meilleure que les termes de bruit seront faibles devant le terme de message. On évalue quantitativement cette qualité par le rapport S/B : \[\frac{\text{Signal}}{\text{Bruit}}=\frac{\text{puissance composante message en sortie du récepteur}}{\text{puissance composante bruit en sortie du récepteur}}\]

3. Modélisation du système de transmission

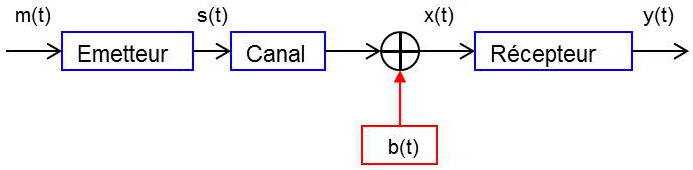Le circuit correspondant est représenté ci-contre.

Le signal \(m(t)\), message à transmettre, a pour largeur de bande B.

Dans le cas général, c’est un signal aléatoire stationnaire et centré.

Sa puissance est de la forme : \[P_m=\int_{-B}^{+B}S_{mm}(f)~df\quad;\quad S_{mm}~:~\text{densité spectrale de puissance}\]

L’émetteur fabrique, à partir de \(m(t)\), le signal modulé : \[s(t)=a(t)~\cos\{2\pi~f_0~t+\varphi(t)\}\]

\(s(t)\) est un signal aléatoire à bande étroite, stationnaire, de largeur de bande B’ centrée sur \(f_0\), c’est-à-dire la fréquence porteuse.

Le canal peut être considéré comme un filtre linéaire de gain constant et de phase linéaire sur une largeur de bande au moins supérieure à B’. Il est donc transparent vis-à-vis du signal (à l’exception d’un retard de propagation et d’un facteur d’atténuation que nous ignorerons dans ce qui suit).

Avec ces hypothèses, le signal reçu au niveau du récepteur est, si l’on néglige la contribution du bruit, égal au signal \(s(t)\) : puissance émise et puissance reçue sont identiques.

Le bruit est additif et indépendant du signal émis. Il peut être modélisé par un processus aléatoire gaussien, centré et stationnaire.

Il est blanc, de densité spectrale (voir Théorie du signal, signaux aléatoires) : \[S_{bb}(f)=\frac{N_0}{2}\qquad\forall f\]

Le récepteur est constitué :

• d’un filtre passe-bande de bande passante égale à B’ de façon à laisser passer les composantes utiles (relatives au signal) et à filtrer les composantes de bruit qui ne sont pas dans la bande du signal ;

• d’un démodulateur ;

• d’un filtre passe-bas de bande passante B de façon à filtrer les composantes du bruit qui ne sont pas dans la bande du message.

Le rapport signal/bruit dépend du type de modulation et de démodulation choisie. Il importe de faire la comparaison de ces différents rapports sur une base commune à tous les systèmes.

4. Rapport S/B en bande de base et gain de modulation

On va supposer que l’on dispose d’une même puissance P pour transmettre le signal modulé. Cette puissance est également la puissance reçue au niveau du récepteur.

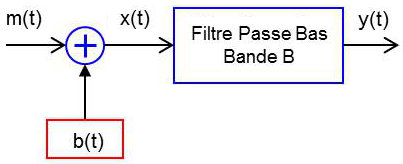Nous voulons comparer les rapports S/B propres à chaque système à celui obtenu dans le système le plus simple, celui où la transmission du message se fait en bande de base, c’est-à-dire sans modulation.

Calculons donc ce rapport de référence \((S/B)_S\) de la transmission en bande de base. \[\left\{ \begin{aligned} x(t)&=m(t)+b(t)\\ y(t)&=m(t)+b'(t) \quad;\quad b'(t)=b(t)~\text{filtré dans}~[-B,~+B] \end{aligned} \right.\]

Densité spectrale de bruit : \[S_{bb'}(f) = \left\{ \begin{aligned} &\frac{N_0}{2}\quad &&-B<f<+B\\ &0 &&\qquad\text{ailleurs} \end{aligned} \right.\]

Puissance de bruit : \[P_b=N_0~B\]

Puissance du signal : \[P_m(t)=P\]

On a donc : \[(S/B)_S=\frac{P}{N_0~B}\]

On posera : \[\gamma=\frac{P}{N_0~B}\]

Ce rapport servira de référence pour comparer les différents types de modulation.

On définit le gain de modulation (ou facteur de mérite) par : \[\eta=\frac{1}{\gamma}~\frac{S}{B}\]

(S/B) étant le rapport signal/bruit pour chaque type de modulation,

P étant la puissance du signal modulé.

5. Informations complémentaires

On pourra se reporter à l’article Bruit de fond dans les systèmes de transmission de la rubrique Électronique.

Le chapitre 6 de conclusion donne une idée de la comparaison physique de la transmission de ce bruit entre les modulations d’amplitude (AM) et de fréquence (MF).