1. Structure de l’ionosphère

1.1. Caractéristiques physiques des couches ionosphériques

Aux altitudes inférieures à 60 km, le nombre de chocs électrons - ions est beaucoup trop élevé, et les ions susceptibles d’exister ont une durée de vie extrêmement courte.

On distingue trois régions :

1. Région D (60 à 100 km) : Faible densité d’ionisation (\(10^8-10^9~e/m^3\)) de jour. Pratiquement inexistante de nuit. Pas de maximum d’ionisation mais peut introduire une atténuation due au nombre élevé de chocs électrons- ions.

2. Région E (100 à 150 km) : Région la plus stable, avec une densité de l’ordre de \(10^{11}~e/m^3\) le jour. Le maximum de densité électronique est appelé fréquence critique de la couche E (entre 3 et 5 MHz). La nuit, seule une ionisation résiduelle demeure.

   Des noyaux d’ionisation super denses peuvent apparaître, mais leur durée de vie est de quelques minutes à quelques heures sous nos latitudes.

3. Région F (à partir de 150 km) : Elle peut être scindée en deux sous-régions en été. \(F_1\) ne présente habituellement pas de maximum d’ionisation et disparaît la nuit. Au-dessus, \(F_2\) possède la densité d’ionisation la plus élevée et joue un rôle fondamental dans la propagation des ondes électromagnétiques.

C’est dans cette dernière région que s’effectuent la plupart des réflexions ionosphériques assurant des liaisons à grande distance. Malheureusement, la couche \(F_2\) est aussi la plus instable, car sa densité d’ionisation ne dépend pas uniquement de l’angle zénithal solaire, contrairement à la région \(E\).

Son maximum d’ionisation est situé entre 300 et 400 km et c’est la seule couche à avoir une concentration ionique appréciable la nuit. Sa fréquence critique peut varier dans de fortes proportions suivant la saison, l’heure et l’activité solaire pour un lieu géographique donné (3 à 15 MHz).

1.2. Modélisation de la structure des couches ionosphériques

La formation et l’évolution des couches ionisées sont déterminées par les vitesses des processus de production et de disparition des électrons. Le problème général du calcul de la production des électrons est compliqué par le fait qu’il faut tenir compte de toutes les radiations du spectre solaire et de tous les constituants atmosphériques.

1.2.1. Modèle initial de Chapman

Chapman a proposé le premier modèle théorique de la densité électronique. Il a adopté les hypothèses simplificatrices suivantes :

• Le faisceau ionisant est formé de rayons parallèles et monochromatiques.

• L’atmosphère contient un seul type de molécules.

• L’atmosphère est isotherme.

• L’atmosphère est stratifiée horizontalement.

• L’absorption est proportionnelle à la profondeur de pénétration.

Dans ces conditions, la densité électronique à l’équilibre est donnée par : \[N(k,\chi)=N_m(\chi)~\exp\Big\{\frac{1}{2}~\big[1-z-\exp(-z)\big]\Big\}\]

Avec :

\[\begin{aligned} z&=\frac{h-h_m(\chi)}{H}\\ h_m(\chi)&=h_{m0}+H~\ln\Big\{\cfrac{1}{\cos(\chi)}\Big\}\\ N_m(\chi)&=N_{m0}~\sqrt{\cos(\chi)}\end{aligned}\]

Où :

• \(\chi\) : angle zénithal solaire

• \(h\) : altitude courante

• \(h_{m0}\) : hauteur du maximum d’ionisation (pour \(\chi=0\))

• \(N_{m0}\) : densité maximale d’ionisation (pour \(\chi=0\))

• \(H\) : hauteur d’échelle de l’atmosphère

Rappelons que \(H=\cfrac{k~T}{mg}\) , avec :

• \(k\) : constante de Boltzmann

• \(T\) : température absolue

• \(m\) : masse moléculaire du gaz

• \(g\) : accélération de la pesanteur

1.2.2. Modèles parabolique et quasi-parabolique

La formule de Chapman est compliquée par la présence d’une exponentielle composée. Dans la plupart des applications, rétro-diffusion ou trajectographie, seule la région située au dessous du maximum d’ionisation est importante, car seuls les rayons qui transitent par cette zone reviennent au sol.

Dans ce cas, seule la portion du profil correspondant à \(z<0\) est utile et il peut être commode de remplacer le profil de Chapman par un profil approché dont l’expression analytique plus simple se prête mieux aux calculs théoriques.

Parmi les nombreux modèles possibles, le modèle parabolique est sans conteste le plus employé. L’équation du profil parabolique se déduit de l’expression première par un développement limité au voisinage du maximum d’ionisation (\(h=h_m\) ou \(r=r_m\) ou \(z=0\)).

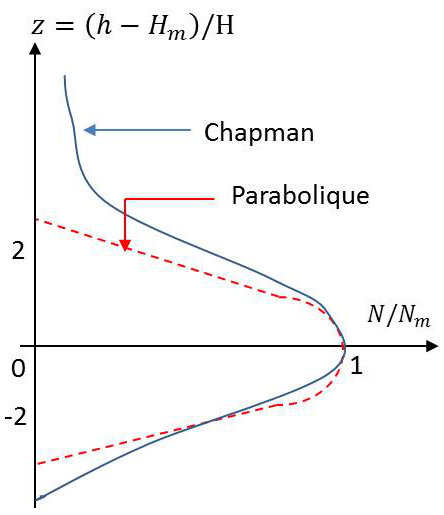Modèle parabolique \[\left\{ \begin{aligned} &N(r,\chi)=N_m~\Big\{1-\Big(\frac{r-r_m}{2H}\Big)^2\Big\}\quad &&|r-r_m|~<2H\\ &N(r,\chi)=0 &&|r-r_m|~\geq 2H \end{aligned} \right.\]

La figure montre que, sans le domaine utile (\(z<0\)), le modèle parabolique est une bonne approximation du modèle de Chapman.

Néanmoins, dans le bas de la couche, les deux profils s’écartent sensiblement.

Cet écart n’est pas gênant lorsque la fréquence émise est bien supérieure à la fréquence critique, ce qui est précisément le cas en rétro-diffusion, car alors le rayon pénètre franchement dans la couche et est peu affecté par la faible ionisation régnant dans le bas de celle-ci.

Modèle quasi-parabolique

D’autre modèles peuvent être également utilisés pour bien se prêter aux simulations sur ordinateur comme le modèle quasi-parabolique direct (le modèle dit inverse n’en différant que par le signe positif): \[\left\{ \begin{aligned} &N(r,\chi)=N_m~\Big\{1-\Big(\frac{r-r_m}{y_m}\Big)^2~\Big(\frac{r_b}{r}\Big)^2\Big\}\quad &&r-r_m<2H\\ &N(r,\chi)=0 &&\text{ailleurs} \end{aligned} \right.\]

• \(r\) : rayon courant (par rapport au centre de la Terre)

• \(N_m\) : densité électronique maximale

• \(r_m\) : rayon du maximum d’ionisation

• \(y_m\) : demi - épaisseur de la couche

• \(r_b=r_m-Y_m\) : rayon de la base de la couche

Ce modèle présente l’avantage d’introduire des équations intégrables dans le calcul des rayons et d’apprécier la précision de calcul dans les programmes de tracé par intégration numérique.

2. Principe de réflexion des ondes radioélectriques

La formation de l’ionosphère provient du phénomène de photo-ionisation de ses constituants, dû au rayonnement ultraviolet, au rayonnement X émis par le soleil et aux trainées météoriques. Il se produit donc des maximums d’ionisation à certaines altitudes

C’est à partir de 60 km d’altitude que la présence de particules électrisées (ionisation) est plus importante, car celles-ci deviennent assez nombreuses pour avoir une influence sur la trajectoire des ondes radioélectriques.

2.1. Formule d’Appleton

La propagation des ondes dans l’ionosphère obéit aux lois de la réfraction en optique (voir la propagation des ondes électromagnétiques), mais en tenant compte des fluctuations du milieu ionosphérique.

La formule de l’indice (complexe) de réfraction de l’ionosphère a été établie pour la première fois par Appleton dès 1926. La formule définitive est connue sous le nom de formule d’Appleton-Hartree : \[n^2=(\mu-j\chi)^2=1-\cfrac{X}{1-jZ-\cfrac{Y_t^2}{2(1-X-jZ)}\pm\sqrt{Y_l^2+\Big\{\cfrac{Y_t}{2(1-X-jZ)}\Big\}^2}}\]

Entrent dans la composition de la formule les paramètres (fréquences) suivants :

• \(f\) : fréquence d’émission

• \(\nu\) : fréquence des collisions

• \(f_p\) : fréquence de plasma

• \(f_g\) : fréquence cyclotron ou gyrofréquence (présence de \(\overrightarrow{B_0}\))

Les paramètres \(X,Y,Z\) étant définis à leur tour par normalisation : \[X=\frac{f_p^2}{f^2}\qquad;\qquad~Y=\frac{f_g}{f}\qquad;\qquad~Z=\frac{\nu}{f}\]

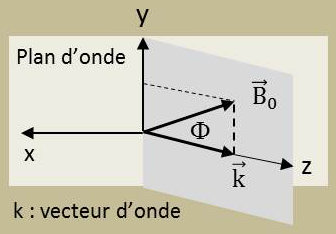\(Y_t\) et \(Y_l\) : composantes tangentielle et longitudinale du vecteur Y : \[Y_t=Y~\sin(\Phi) \quad;\quad Y_l=Y~\cos(\Phi)\]

\(\Phi\) : angle entre l’induction magnétique terrestre \(\overrightarrow{B}_0\) et la normale \(\overrightarrow{T}\) au front d’onde (plan d’égale phase)

La fréquence de plasma \(f_p\) est liée à la densité électronique par la formule : \[f_p=\frac{1}{2\pi}~\sqrt{\frac{N~q_e^2}{\varepsilon_0~m_e}}\]

• \(m_e\) : masse de l’électron

• \(q_e\) : charge de l’électron

• \(\varepsilon_0\) : permittivité du vide

Cette grandeur caractéristique du plasma correspond à la fréquence propre d’oscillation d’ensemble des électrons lorsqu’ils sont momentanément écartés de l’équilibre.

La gyrofréquence \(f_g\) est une caractéristique du mouvement des électrons soumis au champ magnétique terrestre. Elle s’exprime par : \[f_g=\frac{1}{2\pi}~\frac{q_e~B_0}{m_e}\]

2.2. Discussion sur la formule d’Appleton

La formule d’Appleton permet de calculer l’indice de réfraction de phase en un point quelconque de l’ionosphère pour une onde électromagnétique plane monochromatique dont la direction d’incidence par rapport au champ magnétique terrestre est connue.

La formule de l’indice est strictement valable pour un milieu homogène, mais elle peut être appliquée à un milieu variant lentement, c’est-à-dire dans le cas où la vitesse de variation de l’indice de réfraction dans la direction de propagation est petit sur une distance de l’ordre de la longueur d’onde dans le vide.

Lorsque cette condition est vérifiée, il est possible d’utiliser la théorie des rayons de l’optique géométrique.

Notons que la formule de l’indice intègre toutes les caractéristiques fondamentales de l’ionosphère :

• Dispersion : l’indice dépend de la fréquence de l’onde.

• Absorption : l’indice est un nombre complexe, le milieu est dispersif.

• Anisotropie : l’indice dépend de la direction de propagation.

• Biréfringence : la formule de l’indice contient un double signe (\(\pm\)); ainsi, une onde pénétrant dans l’ionosphère est décomposée en deux ondes associées aux modes ordinaire (signe +) et extraordinaire (signe \(-\)).

De plus l’indice dépend de la densité électronique :

• qui varie dans l’espace (milieu hétérogène) ;

• qui varie dans le temps (milieu non stationnaire).

On montre d’autre part que les ondes se propageant dans l’ionosphère sont polarisées et que les facteurs de polarisation transversale \(R_{\pm}\) et \(\sigma_{\pm}\) sont donnés par les relations :

\[\begin{aligned} R_{\pm}&=\frac{E_y}{E_x}=-\frac{H_x}{H_y}=\frac{-j}{Y_l}~\cfrac{Y_t^2}{2(1-X-jZ)}\mp\sqrt{Y_l^2+\Big\{\cfrac{Y_t}{2(1-X-jZ)}\Big\}^2} \\ \sigma_{\pm}&=\frac{E_z}{E_x}=\frac{jY_t~(1-\mu^2)}{1-X-jZ}=\frac{jY_t~X}{(1-X-jZ)(1-jZ-jR_{\pm}~Y_l)}\end{aligned}\]

La composante \(H_z\) du champ magnétique de l’onde est nulle.