1. Impédance ramenée à la distance l de l’extrémité

1.1. Établissement des formules

À la distance \(l\) de l’extrémité, l’onde incidente est \(\exp(\gamma~l)\) fois plus intense qu’en bout de ligne.

La proportion est naturellement inversée pour l’onde réfléchie :

\[\begin{aligned} i_{-l}&=I_{0+}\exp(j~\omega~t+\gamma~l)+I_{0-}\exp(j~\omega~t-\gamma~l)\\ v_{-l}&=V_{0+}\exp(j~\omega~t+\gamma~l)+V_{0-}\exp(j~\omega~t-\gamma~l)\end{aligned}\]

On a une impédance apparente :

\[\begin{aligned} Z_-&=\frac{v_-}{i_-}=\frac{V_{0+}+V_{0-}~\exp(-2~\gamma~l)}{I_{0+}+I_{0-}\exp(-2~\gamma~l)}=Zc~\frac{I_{0+}-I_{0-}~\exp(-2~\gamma~l)}{I_{0+}+I_{0-}\exp(-2~\gamma~l)}\\ Z_-&=Z_c~\frac{1+\rho_0~\exp(-2~\gamma~l)}{1-\rho_0~\exp(-2~\gamma~l)}\end{aligned}\]

avec : \[\rho_0=\frac{V_{0-}}{V_{0+}}=-\frac{I_{0-}}{I_{0+}}\]

En ramenant l’origine à la distance \(l\) de l’extrémité, on peut encore écrire :

\[\begin{aligned} i_{-l}&=(I_{l+}+I_{l-})~\exp(j~\omega~t) &&I_{l\pm}=I_{0\pm}~\exp(\pm\gamma~l)\\ v_{-l}&=(V_{l+}+V_{l-})~\exp(j~\omega~t) &&V_{l\pm}=V_{0\pm}~\exp(\pm\gamma~l)\end{aligned}\]

De même : \[\rho_{-l}=\frac{V_{l-}}{V_{l+}}=-\frac{I_{l-}}{I_{l+}}=\frac{V_{0-}}{V_{0+}}~\exp(-2~\gamma~l)\]

D’où : \[\rho_{-l}=\rho_0~\exp(-2~\gamma~l)\]

On aura également :

\[\begin{aligned} Z_{-l}&=Z_c~\frac{1+\rho_{-l}}{1-\rho_{-l}}\\ \rho_{-l}&=\frac{Z_{-l}-Z_c}{Z_{-l}+Z_c}\end{aligned}\]

Telles sont, jointes aux définitions, les relations fondamentales des lignes.

1.2. Exemples

1) Prenons le cas d’une ligne sans perte, fermée sur une impédance imaginaire pure (contient la ligne ouverte \(Z_L=0\) ou en court-circuit \(Z_L=0\)). On a :

\[\begin{aligned} r&=g=0 &&\gamma=j~\omega~\sqrt{\Lambda~\Gamma}\\ Z_c&=\sqrt{\frac{\Lambda}{\Gamma}} &&Z_0=j~Y\end{aligned}\]

On rappelle que \(\rho_0\) est alors de module unité, soit : \[\rho_0=\frac{Z_0-Z_c}{Z_0+Z_c}=\exp(-2~j~\varphi)\]

Par ailleurs, on peut définir la longueur d’onde : \[\lambda=\frac{2\pi}{\mathcal{J}(\gamma)}=\frac{2\pi}{\omega~\sqrt{\Lambda~\Gamma}}\]

Tous calculs faits, on obtient alors respectivement :

\[\begin{aligned} \rho_{-l}&=\exp\Big\{-2~j~\Big(\varphi+\frac{2\pi~l}{\lambda}\Big)\Big\}\\ Z_{-l}&=j~Z_c~\tan\Big(\varphi-\frac{\pi}{2}+\frac{2\pi~l}{\lambda}\Big)\qquad\text{imaginaire pure}\end{aligned}\]

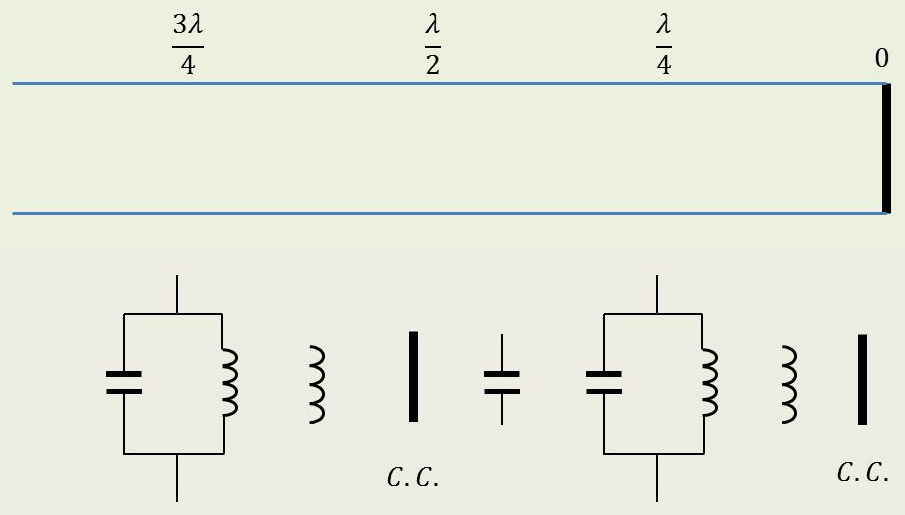2) Le schéma ci-contre représente les diverses impédances mesurées à la distance \(l\) variable d’une ligne mise en court-circuit.

Les courts-circuits intermédiaires (extrémité exclue) sont repérés par l’indice C.C.

La périodicité est en \(\lambda/2\).

La tension paraît selfique ou capacitive selon que la tension est en avance sur le courant ou non.

2. Taux d’ondes stationnaires pour une ligne sans perte

L’onde réfléchie, d’amplitude inférieure ou égale à celle de l’onde incidente interfère avec elle pour donner en certains points des amplitudes maxima ou minima.

On appelle taux d’ondes stationnaires (TOS) la grandeur : \[\tau=\frac{|v_{max}|}{|v_{min}|}\]

Les tensions ont leur amplitude maximums aux endroits où l’onde incidente et l’onde réfléchie se retrouvent en phase : \[|v_{max}|=|V_{0+}|+|V_{0-}|\]

Au contraire : \[|v_{min}|=|V_{0+}|-|V_{0-}|\]

Soit : \[\tau=\frac{|V_{0+}|+|V_{0-}|}{|V_{0+}|-|V_{0-}|}=\frac{1+|\rho_0|}{1-|\rho_0}|\]

Remarquer que \(\tau=\infty\) si \(|\rho_0=1|\).

Par conséquent, on pourra écrire également : \[\tau=\frac{|i_{max}|}{|i_{min}|}\]

Enfin les relations \[V_+=Z_c~I_+\quad;\quad V_-=-Z_c~I_-\]

montrent que les maximums de courant sont situés aux minimums de tension.

—- Fin provisoire de relecture

3. Notions sur l’abaque de Smith

L’abaque de Smith (du nom de son inventeur) est un nomogramme, c’est-à-dire un outil graphique de calcul constitué de courbes graduées entre lesquelles on déplace une règle également graduée.

Il relie le rapport des ondes guidées incidentes et réfléchies le long d’un guide de propagation à la variation d’impédance caractéristique le long de ce guide.

3.1. Origine mathématique

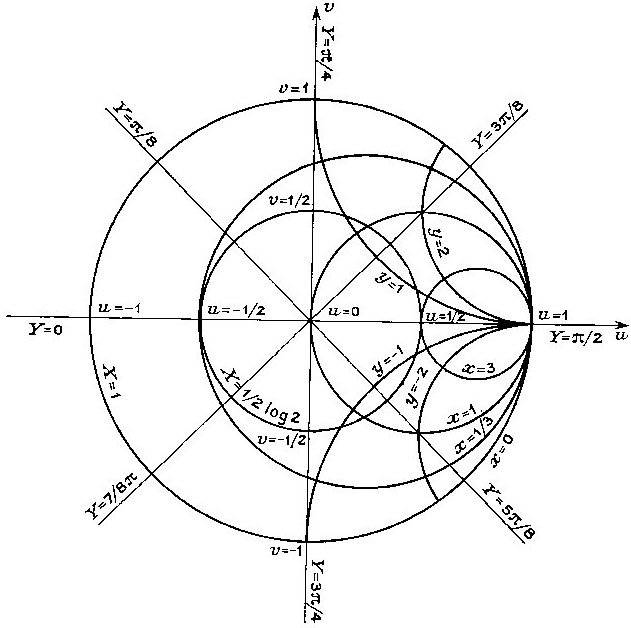L’abaque de Smith trouve son origine dans l’étude des transformations dites conformes de la variable complexe.

Considérons les deux transformations suivantes : \[z=\tanh Z\quad;\quad\rho=-\exp(-2~Z)\]

avec :

\[\begin{aligned} z~&=~x~+~j~y\\ \rho~&=~u~+~j~v\\ Z~&=~X~+~j~Y\end{aligned}\]

De ces deux formules de transformation, nous tirons :

\[\begin{aligned} z~&=~\frac{1+\rho}{1-\rho}\\ \rho~&=~\frac{z-1}{z+1}\end{aligned}\]

Si, dans le plan de la variable \(\rho\) (coordonnées \(u,~v\)), nous traçons les courbes \(X=\text{cte}\) et \(Y=\text{cte} \), nous obtenons un réseau de cercles : \[u^2~+~v^2~=~\exp(-i~X)\]

et un faisceau de droites issues de l’origine : \[\frac{v}{u}~=~-\tan 2~Y\]

Les courbes \(x=\text{cte}\) et \(y=\text{cte}\) sont des faisceaux de cercles orthogonaux :

\[\begin{aligned} \Big(u-\frac{x}{x+1}\Big)^2+v^2&=\frac{1}{(1+x)^2}\\ (u-1)^2+\Big(v-\frac{1}{y}\Big)^2&=\frac{1}{y^2}\end{aligned}\]

Ces courbes, représentées sur la figure ci-dessus, forment ce que l’on appelle le diagramme de Smith.

Si nous considérons une ligne de transmission et si nous désignons par \(z\) l’impédance réduite de la ligne en ce point, \(\rho\) sera en ce même point le coefficient complexe de réflexion, \(X\) représentera l’affaiblissement d’un signal (facile à graduer en décibels) et \(Y\) la rotation de phase de ce même signal.

3.2. Fonctionnalités de l’abaque

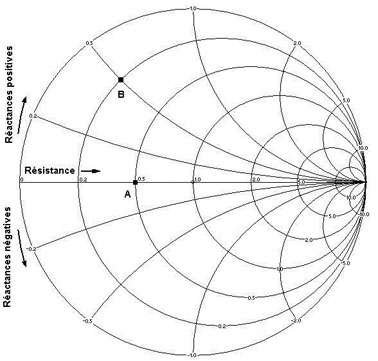Les faisceaux de cercles orthogonaux sont les cercles à résistance constante et à réactance constante.

Le diagramme de Smith permet de passer facilement par des constructions graphiques d’une variable à une autre, en particulier de la variable \(z\) à la variable \(\rho\).

Un point de l’abaque représente donc une impédance. L’abaque donne la valeur de la partie réelle et de la partie imaginaire de l’impédance \(Z\).

L’abaque est ainsi constitué d’un réseau de cercles ou d’arcs de cercle, les isocourbes : parties réelles de \(Z\) constantes et parties imaginaires de \(Z\) constantes.

L’abaque est utilisable pour toutes valeurs de l"impédance caractéristique \(Z_c\), en exprimant sur les graduations la valeur de l’impédance réduite \(z\).

Les tracés doivent être menés à une fréquence unique d’onde guidée, ou à une position unique de la ligne de transmission, et toujours avec les valeurs réduites des impédances, c’est-à-dire en prenant l’impédance caractéristique \(Z_c\) comme unité.

À titre d’exemples:

• Le centre de l’abaque (\(z=1+ j~0\)) représente une résistance pure égale à l’impédance caractéristique \(Z_c\) de la ligne considérée.

• L’axe horizontal représente des résistances pures.

• On peut trouver l’impédance présentée par une ligne de longueur donnée en plaçant sur l’abaque un point représentant la charge en bout de ligne, puis en tournant autour du centre, dans le sens des aiguilles d’une montre, d’un angle fonction de la longueur de la ligne.

Sachant qu’un tour complet correspond à une demi-onde (\(\lambda/2\)) électrique, on voit qu’on retrouve l’impédance de départ au bout d’une demi-onde.

Utilisation de l’abaque pour adapter une source à une charge

On peut aussi utiliser l’abaque de Smith pour concevoir des réseaux d’adaptation d’une source d’impédance complexe à une charge d’impédance complexe, même en l’absence de ligne de transmission. La principale application dans ce cas est l’adaptation entre étages d’amplification RF.

La méthode consiste, à partir du point représentant l’impédance de départ (que ce soit un générateur ou une charge), à lui faire subir les transformations (mise en série ou en parallèles de réactances) pour arriver au point représentant le conjugué de l’impédance d’arrivée.

3.3. Description de l’abaque

L’abaque permet de construire aisément dans le plan complexe \(\rho\) les grandeurs importantes d’une ligne sans pertes d’impédance caractéristique \(Z_c\) fermée sur une impédance \(Z_0\). L’origine est prise en bout de ligne.

Le problème est de construire le nombre complexe : \[\rho=\frac{z-1}{z+1}=1-\frac{2}{z+1}\quad;\quad z=\frac{Z}{Z_c}\]

On passe donc du plan complexe \(z\) au plan complexe \(\rho\) par les opérations suivantes :

• translation (+1) ;

• inversion (puissance 2) ;

• symétrie (autour de l’axe réel) ;

• symétrie (autour de l’origine) ;

• translation (+1).

Ces opérations sont détaillées dans les figures suivantes :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

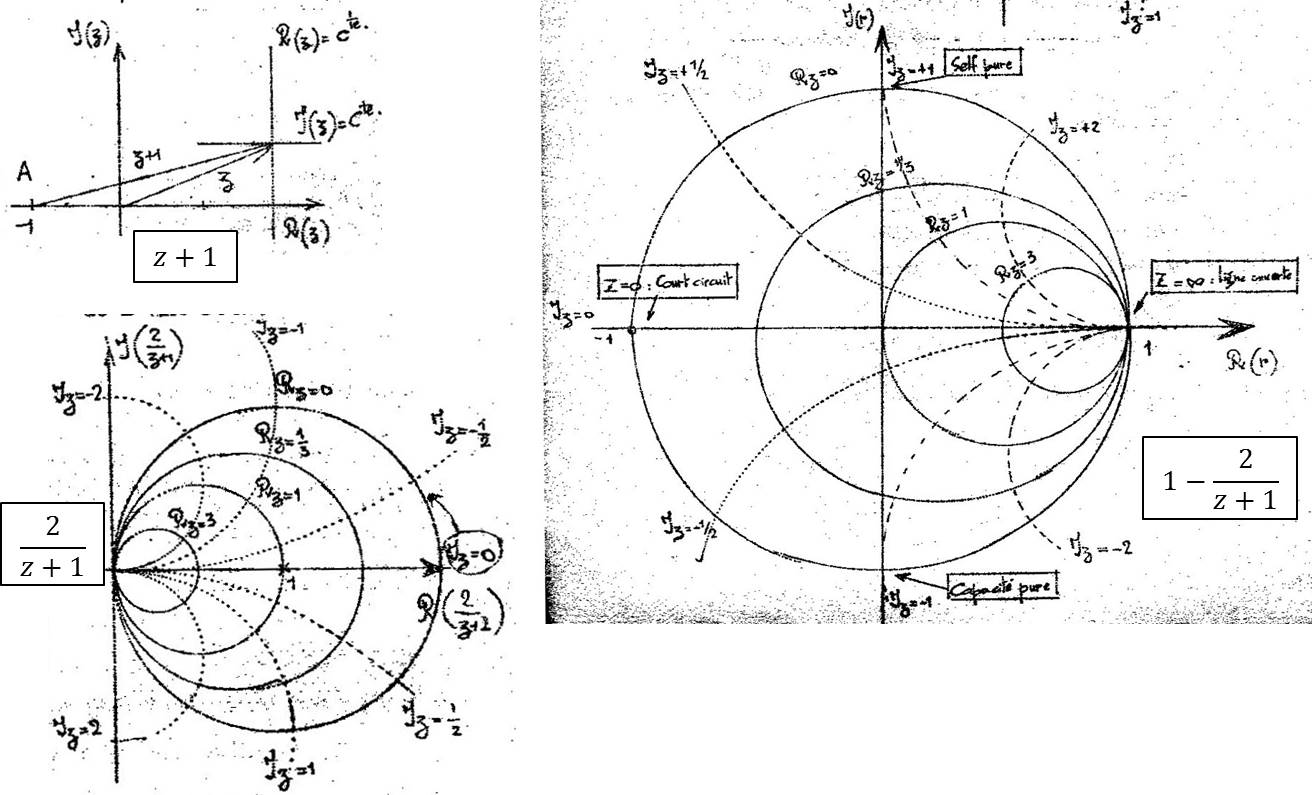
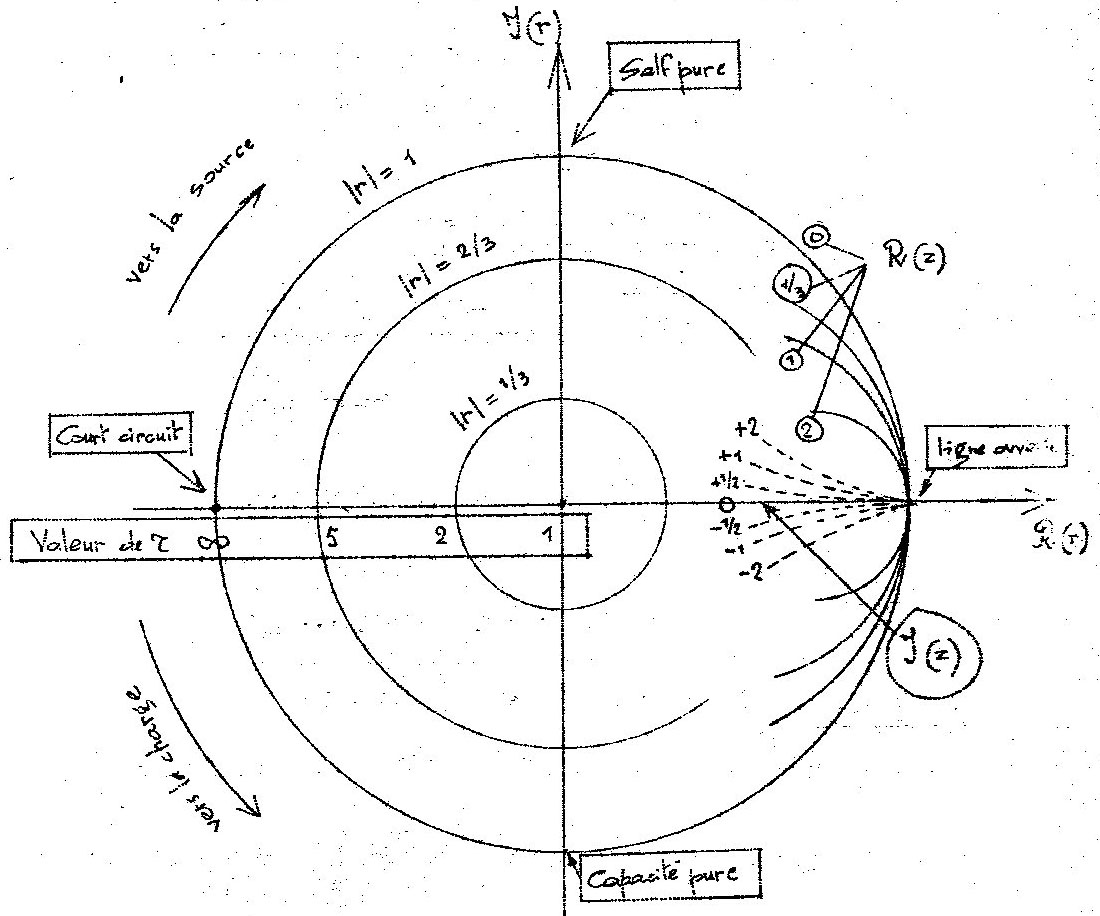
Dans le même plan \(\rho\), on construit facilement le module et l’argument.

D’où la règle :

1. On calcule : \[z_0=\frac{Z_0}{Z_c}\]

2. On construit \(\rho_0\) au croisement des courbes : \[\mathcal{R}(z_0)=\text{cte}\quad;\quad\mathcal{J}(z_0)=\text{cte}\]

3. On tourne sur le cercle \(|\rho|=\text{cte}\) d’autant de tours que de demi-longueurs d’onde, soit d’un angle : \[-2~\theta=-2~\frac{2\pi~L}{\lambda}\]

   afin de construire \(\rho_{-L}\).

4. Ce point est au croisement des courbes : \[\mathcal{R}(z)=\text{cte}~~~~;~~~~\mathcal{J}(z)=\text{cte}\]

   On en déduit \(z_{-L}\), puis \(Z_{-L}=z_{-L}~Z_c\).

5. On mesure enfin.

4. Formule très pratique pour un calcul d’impédance

Voici une formule qui fait suite au § 1.1 (exploitation des exponentielles), donnée ici sans démonstration.

On sait que : \[\gamma=\alpha+j~\beta\]

avec : \[\beta=\frac{2\pi}{\lambda}\]

Pour une ligne sans pertes, \(\alpha=0\).

On désigne par \(z_l\) l’impédance réduite de la charge en bout de ligne.

Pour la détermination de \(z\) à une distance \(d\) de cette charge, on établit alors la relation par un calcul classique : \[z=\frac{\tanh(\gamma~d)+z_l}{1+z_l~\tanh(\gamma~d)}\]