1. Champ magnétique et champ électrique

Nous donnons les formules essentielles sans démonstrations (à partir des équations de Maxwell).

1.1. Champ magnétique créé par un élément de courant dans le vide

Expression du champ élémentaire : \[\overrightarrow{dH}=\overrightarrow{C}~d\tau\wedge\frac{\overrightarrow{r}}{4\pi~r^3}+\frac{1}{c}~\frac{\partial\overrightarrow{C}}{\partial t}~d\tau\wedge\frac{\overrightarrow{r}}{4\pi~r^2}\]

• \(\overrightarrow{C}\) : vecteur densité de courant

• \(d\tau\) : élément de volume

• \(r\) : distance du point à l’élément de courant

• \(c\) : célérité de l’onde

Le premier terme \(\overrightarrow{dH_1}\) est le champ élémentaire de Laplace.

Le deuxième terme \(\overrightarrow{dH_2}\), qui ne décroît qu’en \(1/r\), est le champ élémentaire dû aux courants variables.

Si \(C\) est sinusoïdal, le second terme est en quadrature avec le premier (dérivation \(\partial/\partial t\)). Les deux termes ont alors la même amplitude si : \[\omega~r=c\quad\Rightarrow\quad r=\frac{\lambda}{2\pi}\]

1.2. Champ électrique créé par une répartition variable de charges

En opérant avec un calcul analogue à celui du cas précédent : \[\overrightarrow{dE}=\frac{d\tau}{4\pi~\varepsilon_0}~\Big\{\rho~\frac{\overrightarrow{r}}{r^3}+\frac{1}{c^2}~\frac{\overrightarrow{r}}{r^2}\wedge\Big(\frac{\overrightarrow{r}}{r}\wedge\frac{\overrightarrow{\partial C}}{\partial t}\Big)\Big\}\]

\(\qquad\rho\) : densité de charges

La première composante \(\overrightarrow{dE_1}\) est la composante coulombienne.

La deuxième composante \(\overrightarrow{dE_2}\) est due aux courants variables et ne décroît qu’en \(1/r\).

On note que : \[\overrightarrow{dE_2}=\frac{1}{\varepsilon_0~c}~\overrightarrow{dH_2}\wedge\frac{\overrightarrow{r}}{r}~ =~\sqrt{\frac{\mu_0}{\varepsilon_0}}~\overrightarrow{dH_2}\wedge\frac{\overrightarrow{r}}{r}\]

On retrouve la même relation que pour une onde plane. Ceci n’est pas étonnant, car à grande distance seuls les termes \(E_2\) et \(H_2\) comptent et l’onde est sensiblement plane.

2. Dipôle

Le dipôle neutre est constitué de deux charges \(\pm q\) distantes de \(l_0\).

On définit un moment dipolaire \(p_0=q~l_0\).

2.1. Champ d’un dipôle oscillant

Considérons ce dipôle vibrant selon la direction \(\overrightarrow{p_0}\).

Le centre des charges est supposé fixe. Leur distance est notée : \[l=l_0~\exp(j~\omega~t)\]

Leur vitesse relative est : \[v=\frac{dl}{dt}=j~\omega_0~l_0\]

Le moment dipolaire est alors noté : \[\overrightarrow{p}=\overrightarrow{p_0}~\exp(j~\omega~t)\]

On démontre que le courant élémentaire (densité \(\overrightarrow{C}\)), équivalent à \(qv\), crée le champ magnétique : \[\overrightarrow{H}=\frac{j~\omega}{4\pi}~\overrightarrow{p}\wedge\frac{\overrightarrow{r}}{r}~\Big(1-\frac{j~\omega~r}{c}\Big)~\exp\Big(-\frac{j~\omega~r}{c}\Big)\]

Nota : \[\frac{\omega~r}{c}=\frac{2\pi~r}{\lambda}\]

La densité de charge fluctuante crée un champ électrique qui est la somme du champ dipolaire électrostatique retardé et du champ créé par \(\partial\overrightarrow{C}/\partial t\) : \[\overrightarrow{E}=-\frac{1}{4\pi~\varepsilon_0}~\Big\{\overrightarrow{\text{grad}}\Big(\frac{\overrightarrow{p}\cdot\overrightarrow{r}}{r^3}\Big)-\frac{\omega^2}{r~c^2}~\frac{\overrightarrow{r}}{r}\wedge\Big(\frac{\overrightarrow{r}}{r}\wedge\overrightarrow{p}\Big)~\exp\Big(-\frac{j~\omega~r}{c}\Big)\Big\}\]

2.1.1. Courte distance ou basse fréquence

Le cas correspond à : \[r~\ll~\lambda\qquad\text{ou}\qquad\frac{\omega~r}{c}~\ll~1\]

On a alors :

\[\begin{aligned} \overrightarrow{E}~&\approx~-\frac{1}{4\pi~\varepsilon_0}~\overrightarrow{\text{grad}}\Big(\frac{\overrightarrow{p}\cdot\overrightarrow{r}}{r^3}\Big) =\frac{1}{4\pi~\varepsilon_0}~\Big\{\frac{3~\overrightarrow{r}~(\overrightarrow{p}\cdot\overrightarrow{r})}{r^5}-\frac{\overrightarrow{p}}{r^3}\Big\}\\ \overrightarrow{H}~&\approx~\frac{1}{4\pi}~j~\omega~\overrightarrow{p}\wedge\frac{\overrightarrow{r}}{r^3}\end{aligned}\]

On trouve le champ électrique du doublet et le champ magnétique de Laplace. C’est l’approximation quasi-stationnaire.

On remarquera que :

\[\begin{aligned} &\overrightarrow{E}\cdot\overrightarrow{H}=0\qquad\text{(vecteurs en quadrature)}\\ &E ~\text{décroît en}~\frac{1}{r^3}\quad;\quad H ~\text{décroît en}~\frac{1}{r^2}\end{aligned}\]

2.1.2. Grande distance ou haute fréquence

Le cas correspond à : \[r~\gg~\lambda\qquad\text{ou}\qquad\frac{\omega~r}{c}~\gg~1\]

On a alors :

\[\begin{aligned} \overrightarrow{E}~&\approx~\frac{\omega^2}{4\pi~\varepsilon_0~c^2~r}~\frac{\overrightarrow{r}}{r}\wedge\Big(\overrightarrow{p}\wedge\frac{\overrightarrow{r}}{r}\Big)~\exp\Big(-j~\frac{\omega~r}{c}\Big)\\ \overrightarrow{H}~&\approx~\frac{\omega^2}{4\pi~c~r}~\frac{\overrightarrow{r}}{r}\wedge\overrightarrow{p}~\exp\Big(-j~\frac{\omega~r}{c})\end{aligned}\]

On a donc : \[\overrightarrow{E}~\approx~-\sqrt{\frac{\mu_0}{\varepsilon_0}}~\frac{\overrightarrow{r}}{r}\wedge\overrightarrow{H} \quad\Rightarrow~\quad\overrightarrow{E}~\bot~\overrightarrow{H}\]

2.2. Résistance de rayonnement du dipôle

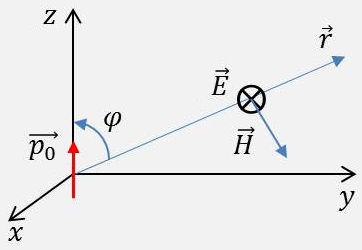À grande distance : \[\overrightarrow{R}_{eff}=\frac{\overrightarrow{E}\wedge\overrightarrow{H^*}}{2}=\sqrt{\frac{\mu_0}{\varepsilon_0}}~H_{eff}^2~\frac{\overrightarrow{r}}{r}\]

Soit : \[\overrightarrow{R}_{eff}=\frac{\omega^4~p_{eff}^2}{16\pi^2~r^2~c^2}~\sqrt{\frac{\mu_0}{\varepsilon_0}}~\sin^2\varphi~\frac{\overrightarrow{r}}{r}\]

\(\overrightarrow{r},~\overrightarrow{E},~\overrightarrow{H}\) sont distribués à grande distance comme dans une onde plane. \(R\) est en \(1/r^2\). On est à flux constant.

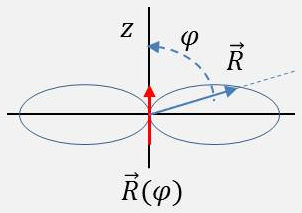L’énergie rayonnée dans un angle solide élémentaire est proportionnelle à \(\sin^2\varphi\).

Puissance totale rayonnée : \[W=\frac{\omega^4~p_{eff}^2}{16\pi^2~r^2~c^2}~\sqrt{\frac{\mu_0}{\varepsilon_0}}~\int_0^{\pi}2\pi~\sin^3\varphi~d\varphi\]

En rappelant que :

• \(q~l\) : moment du dipôle

• \(i=j~\omega~q\) : élément de courant

\[W=\frac{\omega^4~p_{eff}^2}{16\pi^2~r^2~c^2}~\sqrt{\frac{\mu_0}{\varepsilon_0}}\]

Que l’on peut encore écrire : \[W=\frac{2\pi}{3}~\sqrt{\frac{\mu_0}{\varepsilon_0}}~\frac{l^2}{\lambda^2}~i_{eff}^2=790~\frac{l^2}{\lambda^2}~i_{eff}^2\]

On écrit encore :

\[\begin{aligned} W&=R_r~i_{eff}^2\\ R_r&=\frac{2\pi}{3}~\sqrt{\frac{\mu_0}{\varepsilon_0}}~\frac{l^2}{\lambda^2}=790~\frac{l^2}{\lambda^2}\end{aligned}\]

\(R_r\) : résistance de rayonnement du dipôle

3. Électron

3.1. Mouvement induit d’un électron

Rappelons l’équation classique du mouvement de l’électron : \[m~\frac{d^2x}{dt^2}+f~\frac{dx}{dt}+m~\omega_0^2~x=e~E_0~\exp(j~\omega~t)\]

• \(f\) : coefficient de frottement (non précisé)

• \(\omega_0\) :  pulsation de résonance de l’électron lié

• \(-m~\omega_0^2~x\) : force de rappel vers la position d’équilibre

• \(k=m~\omega_0^2\) : constante de rappel

Il vient :

\[\begin{aligned} x&=x_0~\exp(j~\omega~t)\\ x_0&=\frac{e~E_0}{m~(\omega_0^2-\omega^2)+j~\omega~f}\end{aligned}\]

Cas particulier électrons fortement liés : \[\omega_0\gg\omega~;~\sqrt{\frac{\omega~f}{m}}\quad\Rightarrow\quad x_0\approx\frac{e~E_0}{m~\omega_0^2}\]

Cas particulier électrons libres : \[x_0\approx\frac{e~E_0}{m~\omega_0^2}\]

3.2. Rayonnement diffusé par les électrons

Électrons liés : \[W_{lie}=\frac{1}{12\pi}~\sqrt{\frac{\mu_0}{\omega_0}}~\frac{e^4~\omega^4}{m^2~c^2~\omega_0^4}~E_0^2\]

Électrons libres : \[W_{libre}=\frac{1}{12\pi}~\sqrt{\frac{\mu_0}{\omega_0}}~\frac{e^4}{m^2~c^2}~E_0^2\]

Comparons à l’intensité de l’onde incidente (flux de puissance à travers une surface unité) :

\[\begin{aligned} \mathcal{J}&=\frac{1}{2}~E_0~H_0=\frac{1}{2}~\sqrt{\frac{\varepsilon_0}{\mu_0}}~E_0^2\\ \frac{W_{lie}}{\mathcal{J}}&=\frac{1}{6\pi}~\frac{\mu_0}{\varepsilon_0}~\frac{e^4}{m^2~c^2}~\Big(\frac{\omega}{\omega_0}\Big)^4 \\ \frac{W_{libre}}{\mathcal{J}}&=\frac{1}{6\pi}~\frac{\mu_0}{\varepsilon_0}~\frac{e^4}{m^2~c^2}\end{aligned}\]

La deuxième formule traduit la loi de Rayleigh. La puissance diffractée est proportionnelle à \(\omega^4\). Elle explique la répartition de la lumière visible diffusée par un gaz (bleu du ciel).

La troisième explique la diffusion des rayons X (\(\omega\gg\omega_0\)). Elle expliquerait également la polarisation et la répartition de la puissance diffusée.

3.3. Rayonnement d’un électron oscillant

Rappelons l’expression du champ électromagnétique rayonné à grande distance par le dipôle :

\[\begin{aligned} \overrightarrow{p}&=\overrightarrow{p}_0~\exp(j~\omega~t)\\ \overrightarrow{H}&=\frac{\omega}{2~r~\lambda}~\frac{\overrightarrow{r}}{r}\wedge\overrightarrow{p}_0~\exp\Big\{j~\omega\Big(t-\frac{r}{c}\Big)\Big\}\\ \overrightarrow{E}&=-\sqrt{\frac{\mu_0}{\varepsilon_0}}~\frac{\overrightarrow{r}}{r}\wedge\overrightarrow{H}\end{aligned}\]

Sachant que l’on a ici : \[\overrightarrow{p}=e~\overrightarrow{x}\quad;\quad x=x_0~\exp(j~\omega~t)\]

On obtient, pour la puissance rayonnée : \[W=\frac{\omega^4~p_0^2}{16\pi^2~r^2~c^2}~\sqrt{\frac{\mu_0}{\varepsilon_0}}=\frac{1}{12\pi}~\sqrt{\frac{\mu_0}{\varepsilon_0}}~\frac{e^2~\omega^4~x_0^2}{c^2}\]

3.4. Propriétés électriques d’un plasma

Le plasma est constitué par des ions et des électrons supposés libres. Pratiquement, seuls les électrons qui sont légers sont mis en mouvement par le champ électromagnétique incident.

S’il se trouve \(N\) électrons par unité de volume, l’intensité de polarisation est : \[P=-N~e~x=-\frac{N~e^2}{m~\omega^2}~E\]

Le milieu se comporte comme s’il possède la constante diélectrique : \[\varepsilon_r=1-\frac{N~e^2}{m~\omega^3}\]

Soit un indice de réfraction \[n=\sqrt{\varepsilon_r}~\approx~1-\frac{N~e^2}{2~m~\omega^2}~<~1\]

Il peut y avoir réflexion totale pour les ondes longues. C’est le cas de la couche de Kennely-Heaviside réfléchissant les ondes kilométriques en haute atmosphère.

4. Doublet de Hertz : une formule pratique

Le doublet de Hertz est une antenne filaire de longueur très faible devant la longueur d’onde \(\lambda\) ; elle est donc parcourue par un courant constant.

À une distance \(r\) d’un doublet de Hertz de longueur \(dx\) dans une direction faisant un angle \(\theta\) avec le doublet, on observe un champ électrique élémentaire \(\overrightarrow{dE}\) tel que (équations de Maxwell) : \[dE=\frac{60\pi}{r~\lambda}~I~\exp\Big\{j~\omega\Big(t-\cfrac{r}{v}\Big)\Big\}~\sin\theta~dx\]

avec : \(I~\exp(j~\omega~t)\) : courant à l’instant \(t\) dans le doublet

5. Rayonnement d’une antenne demi-onde

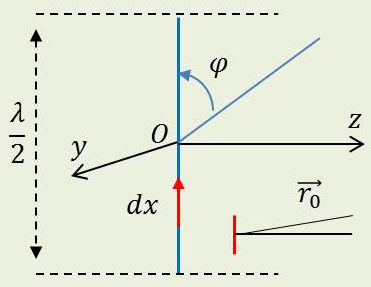On suppose que le courant dans l’antenne est : \[i=-i_0~\cos\frac{2\pi~x}{\lambda}~\cos(\omega~t)\quad;\quad|x|\ll\frac{\lambda}{4}\]

On peut assimiler cette antenne à une suite de dipôles : \[\overrightarrow{p}=\frac{di}{dt}~\overrightarrow{dx}\]

Analytiquement : \[\overrightarrow{p}=\frac{i_0}{\omega}~\cos\frac{2\pi~x}{\lambda}~\sin(\omega~t)~\overrightarrow{dx}\]

En intégrant sur \(dx\) : \[\overrightarrow{H}=\frac{\omega~i_0}{4\pi~c}~\int_{-\lambda/4}^{+\lambda/4}~\frac{\overrightarrow{r}}{r^2}\wedge\overrightarrow{dx}~\cos\frac{2\pi~x}{\lambda}~\sin\Big(\omega~t-\frac{2\pi~r}{\lambda}\Big)\]

Posons : \[\overrightarrow{r}_0=\overrightarrow{x}+\overrightarrow{r}\quad;\quad r_0\approx r+x~\cos\varphi\]

On obtient, à grande distance (\(r_0\gg\lambda\)) : \[H=H_y\approx\frac{\omega~i_0}{4\pi~c}~\Big\{\int_{-\lambda/4}^{+\lambda/4}dx~\cos\frac{2\pi~x}{\lambda}~\cos 2\pi\Big(\frac{x~\cos\varphi}{\lambda}\Big)\Big\}~\frac{\sin\Big(\omega~t-\cfrac{2\pi~r_0}{\lambda}\Big)}{r_0}~\sin\varphi\]

Ou encore :

\[\begin{aligned} H&\approx-\frac{i_0}{2\pi~r_0}~\frac{\cos\Big(\cfrac{\pi}{2}~\cos\varphi\Big)}{\sin\varphi}~\sin\Big(\omega~t-\frac{2\pi~r_0}{\lambda}\Big)\\ E&\approx\sqrt{\frac{\mu_0}{\varepsilon_0}}~H=\mu_0~c~H=-\sqrt{\frac{\mu_0~i_0}{\varepsilon_0~2\pi~R_0}}~\frac{\cos\Big(\cfrac{\pi}{2}~\cos\varphi\Big)}{\sin\varphi}~\sin\Big(\omega~t-\frac{2\pi~r_0}{\lambda}\Big)\end{aligned}\]

D’où le module du vecteur de Poynting : \[R_{eff}=\sqrt{\frac{\mu_0}{\varepsilon_0}}~\frac{i_{eff}^2}{2\pi^2~r_0^2}~\frac{\cos^2\Big(\cfrac{\pi}{2}~\cos\varphi\Big)}{\sin^2\varphi}\]

Et la puissance rayonnée :

\[\begin{aligned} \langle~P~\rangle&=R_r~i_{eff}^2\\ R_r&=\frac{1}{\pi}~\sqrt{\frac{\mu_0}{\varepsilon_0}}~\int_0^{\pi}\frac{\cos^2\Big(\cfrac{\pi}{2}~\cos\varphi\Big)}{\sin\varphi}~d\varphi\end{aligned}\]

Le calcul donne \(R_r=72,6~\Omega\).

Note

Rappelons l’expression du vecteur complexe de Poynting (cf. équations de Maxwell) : \[\overrightarrow{R}_{eff}=\frac{\overrightarrow{E}\wedge\overrightarrow{H^*}}{2}\]

Rappelons également que le flux de ce vecteur permet de déterminer la puissance moyenne perdue par effet joule, les pertes magnétiques et diélectriques, à savoir respectivement (intégration dans un volume \(v\)) : \[\iiint\gamma~E_{eff}^2~d\tau\quad;\quad\iiint\omega~\mu~H_{eff}^2~d\tau\quad;\quad\iiint\varepsilon~E_{eff}^2~d\tau\]

6. Antennes

Nous ne donnons ici que des éléments de base pour la propagation hertzienne, donc d’une présentation très succincte du principe de l’antenne.

6.1. Directivité

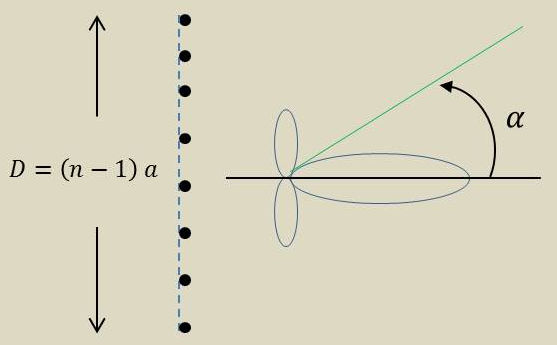Les dipôles élémentaires constituant les antennes interfèrent entre eux pour diminuer la puissance émise dans certaines directions et pour la renforcer dans d’autres.

Ainsi, une famille de \(n\) sources sphériques en phase disposées sur un segment de droite et espacées de \(a\) permet d’obtenir le diagramme de rayonnement ci-contre.

Toute la puissance se trouve alors pratiquement dans l’angle \(\alpha\) tel que : \[\sin\alpha=\frac{\lambda}{D}\]

6.2. Théorème des aériens rectilignes

Soit \((x)dx\) l’intensité dans la direction \(\theta\) et à la distance \(r\) de la source sphérique constituée par l’élément \(dx\).

Pour l’intensité totale de l’aérien rectiligne, le diagramme de rayonnement en coordonnées polaires est : \[A(\theta)=\int_{-\infty}^{+\infty}\exp\Big(j~\frac{2\pi~x~\sin\theta}{\lambda}\Big)~dx\]

D’où, par inversion de Fourier : \[a(x)=\int_{-\infty}^{+\infty}A\Big(\frac{\sin\theta}{\lambda}\Big)~\exp\Big(-j~\frac{2\pi~x~\sin\theta}{\lambda}\Big)~d\Big(\frac{\sin\theta}{\lambda}\Big)\]

Les fonctions \(a(x)\) et \(A\Big(\cfrac{\sin\theta}{\lambda}\Big)\) sont des images dans la transformation de Fourier.

En particulier, le rayonnement \(a\Big(\cfrac{\sin\theta}{\lambda}\Big)\) est obtenu par la répartition des sources sphériques \(A(-x)\).

6.3. Types d’antennes et alimentation

L’antenne demi-onde (\(R_r=73~\Omega\)) est attaquée au centre par une ligne d’impédance caractéristique \(\sqrt{L/\Gamma}\).

On évite les ondes stationnaires dans la ligne par réflexion à son extrémité si : \[\sqrt{\frac{L}{\Gamma}}=73~\Omega\]

On satisfait ainsi à la condition d’adaptation d’impédances (en bout de ligne \(v=R_r~i\)).

Autres types d’antennes : cadres, réseaux, antennes diélectriques...

7. Polarisation du rayonnement

La polarisation du rayonnement s’obtient en ajoutant les champs retardés produits par les courants élémentaires à grande distance (\(r\gg\lambda\)) :

\[\begin{aligned} \overrightarrow{dH}&=j~\omega~i~\frac{\overrightarrow{dl}\wedge\overrightarrow{r}}{4\pi~r^2~c}~\exp\Big(-j~\frac{2\pi~r}{\lambda}\Big)\\ \overrightarrow{dE}&=\sqrt{\frac{\mu_0}{\varepsilon_0}}~\overrightarrow{dH}\wedge\frac{\overrightarrow{r}}{r}\end{aligned}\]

7.1. Réciprocité

Une antenne réceptrice est excitée à la résonance par le champ électromagnétique incident. Des conditions de polarisation sont à respecter.

Intégrons le champ sur une antenne demi-onde : \[V=\frac{\lambda}{2}~E\cos\theta\]

L’antenne rayonne, à son tour, la puissance diffractée : \[\frac{V^2}{R_r}=\frac{\lambda^2~E^2}{4}~\frac{\cos^2\theta}{R}\]

La puissance incidente par unité de surface est : \[\frac{\varepsilon_0~c~E^2}{2}\]

L’antenne recueille donc la puissance distribuée sur une surface dite surface de captation : \[S=\frac{\lambda^2}{4}~\frac{E^2}{R_r}~\frac{2~\cos^2\theta}{\varepsilon_0~c~E^2}=\frac{\lambda^2~\cos^2\theta}{2~R_r~c~\varepsilon_0}\]

C’est-à-dire : \[S=\frac{30~\pi}{73}~\lambda^2~\cos^2\theta\]

On reconnaît l’aire d’un cercle de diamètre \(1,3~\lambda~\cos\theta\).

La puissance peut être recueillie par une ligne si possible adaptée.

7.2. Cornets

Les ondes décimétriques et centimétriques sont émises ou reçues parfois par des cornets.

La polarisation dépend du type d’onde transmise.

Le rôle du cornet est d’éviter la discontinuité d’impédance à la sortie du guide qui débouche sur l’espace infini.