1. Introduction

1.1. Une nouvelle impulsion

Les transmissions à très haut débit exigent des impulsions lumineuses d’information intenses, courtes, spectralement pures, les moins bruitées possibles, injectées dans une fibre optique. Une telle impulsion existe : c’est la solution dite solitaire d’une forme non linéaire de l’équation de Schrödinger, désigné sous le nom de soliton.

C’est l’exploitation d’un phénomène de non linéarité, l’effet Kerr de l’optique physique, qui a permis de parvenir à cette forme remarquable de l’équation de Schrödinger.

1.2. Image et métaphore

L’image

« […] Alors que j’observais le mouvement d’un bateau que deux chevaux tiraient rapidement dans un canal étroit, celui-ci vint à s’arrêter tout à coup. Mais pas la masse d’eau qu’il avait mise en mouvement dans le canal.

« Celle-ci s’accumula autour de la proue dans un état de violente agitation, laissa tout à coup le bateau en arrière, se mit à cheminer en avant avec une grande vitesse, sous la forme d’une seule grande ondulation, de surface arrondie, lisse et parfaitement déterminée.

« Cette onde continua sa marche dans le canal sans que sa forme et sa vitesse parussent s’altérer en rien.

« Je la suivis à cheval et la retrouvai, cheminant encore avec une vitesse de 8 à 9 milles à l’heure et conservant sa figure initiale (environ 30 pieds de longueur sur 1 pied à 1,5 pied de hauteur).

« La hauteur de l’onde diminuait graduellement, et après l’avoir suivie pendant un mille ou deux, je la perdis dans les sinuosités du canal. »

Sir J. Scott Russel, Edimburgh-Glasqow, 1834

Cette onde s’appela alors l’onde solitaire de Russel. Elle allait faire du chemin.

La métaphore

La métaphore est une idée de L. F. Mollenauer et G. Evangelides (firme ATT) et qui rend bien compte du phénomène et de son environnement de manière très simple.

Un groupe de coureurs évoluent sur un milieu déformable, un matelas par exemple. Le coureur le plus rapide est en tête, mais il doit gravir en permanence la dépression mobile provoquée par le poids du groupe, ce qui l’empêche de se détacher du groupe. À contrario, la descente permanente dans cette même dépression évite au moins rapide des coureurs de se faire rapidement distancer.

On peut dire que l’interaction du groupe avec le milieu tend à corriger les différences de vitesse entre les coureurs. On peut dire aussi que le contrôle séparé du poids du groupe, de la distance entre coureurs et de la disparité des conditions physiques permet la formation d’un peloton stable au comportement quasi-corpusculaire.

2. Équation de Schrödinger non linéaire

2.1. Origine physique : l’effet Kerr de l’optique

L’intensité du champ électrique modifie l’indice de réfraction du matériau diélectrique : \[n=n_0(\omega)+n_2~|E|^2\qquad[1]\]

• \(n_2\) : coefficient de Kerr

Valeur typique pour une fibre de verre : \(n_2=1,2\times 10^{-22}~\rm m^2~V^{-2}\)

L’effet Kerr traduit une déformation des orbites électroniques dans les molécules du verre. Le temps de réponse est donc extrêmement court, de l’ordre de la femtoseconde (\(10^{-15}~\)s).

Prenons l’exemple d’une fibre standard de section de 60 cm², d’une puissance de 100 mW, produisant dans la fibre un champ électrique de l’ordre de \(10^6~\rm V~m^{-1}\). L’indice de réfraction s’accroit d’un facteur de l’ordre de \(10^{-10}\). En raison du terme non linéaire, le nombre d’onde varie d’un facteur : \[\Delta k=n_2~|E|^2~\frac{\omega}{c}=n_2~|E|^2~\frac{2\pi~f}{\lambda~f}=n_2~|E|^2~\frac{2\pi}{\lambda}\qquad[2]\]

Ce changement d’indice affecte la propagation de la lumière, mais, dans certaines conditions, il est de nature à corriger les effets de dispersion associés aux différentes composantes spectrales de la lumière qui elles aussi se propagent avec des vitesses différentes. Il en résulte des impulsions de lumière d’enveloppe constante appelés solitons. Les non-linéarités corrigeant la dispersion, c’est donc bien le signal lui-même qui corrige les imperfections du canal.

2.2. Forme de l’équation non linéaire de Schrödinger

Le mot soliton a été employé pour la première fois en 1964 par Zabusky et Kruskall qui ont essayé de résoudre l’équation de Korterveg de Vries (dite KDV) qui modélise, depuis le XIX\(^\text{ième}\) siècle le phénomène de propagation d’une vague à la surface de l’eau.

Cette équation décrit la propagation de l’enveloppe du soliton à partir de l’équation non linéaire de Schrödinger en prenant une amplitude complexe \(q(x,~t)\) : \[j~\frac{\partial q}{\partial x}+\frac{1}{2}~\frac{\partial^2q}{\partial t^2}+|q^2|~q=0\qquad[3]\]

• \(x\) représente distance dans la direction de propagation.

• \(t\) représente le temps.

3. Soliton en ligne

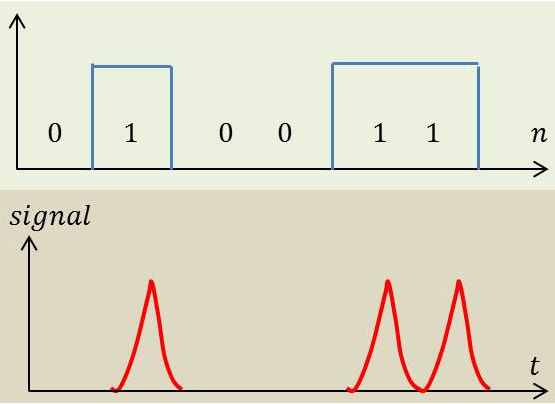Pour les systèmes de transmission qui utilisent les solitons, il est naturel que la succession de 0 et de 1 soit codée par absence ou présence de soliton au sein d’un bit.

Cette façon de transmettre l’information est différente de la modulation classique en intensité où l’information est associée à une répartition uniforme d’intensité sur tout l’intervalle du temps bit.

À cause des non-linéarités de la fibre, il est possible que des interférences inter-symboles se produisent. Pour les éliminer, nous pouvons choisir une durée d’impulsion relativement faible devant l’intervalle séparant deux solitons successifs.

Si l’on tient compte de l’atténuation entre chaque amplificateur, on s’éloigne du soliton idéal.

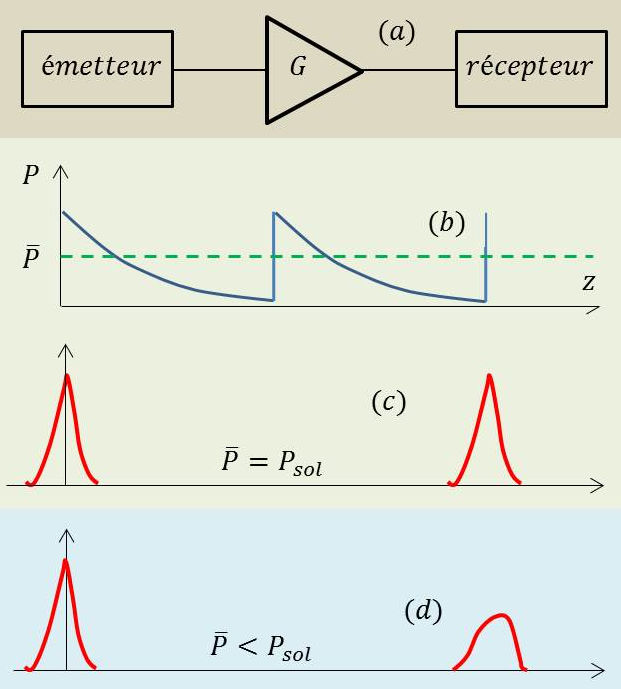On peut démontrer que des solitons appelés solitons moyens peuvent se propager. La puissance moyenne des solitons dans la fibre est égale à celle du soliton idéal (a)

La puissance optique du soliton varie périodiquement entre une valeur maximale et une valeur minimale.

On peut parler d’une puissance moyenne \(\overline{P}\) qui caractérise globalement la propagation du soliton. Cette puissance moyenne doit être égale à celle du soliton théorique (dans la fibre à atténuation nulle).

Quand la puissance optique dépasse la valeur moyenne, les impulsions subissent une petite contraction. Et vice versa, quand la puissance est inférieure à la valeur moyenne (léger élargissement). En valeur moyenne, les impulsions conservent leur durée initiale (c).

Par contre, si la puissance moyenne \(\overline{P}\) est trop faible, les effets non-linéaires seront insuffisants pour compenser les effets de dispersion et le soliton s’élargira (d).

On peut dire que la puissance du soliton est proportionnelle à la dispersion chromatique présentée par la fibre.

4. Source à solitons

La source à solitons est l’élément critique d’un système à solitons. Elle réalise deux fonctions en cascade :

• la génération du train régulier d’impulsions optiques à un taux égal au débit à transmettre ;

• la modulation par le train binaire d’information par masquage de ces informations.

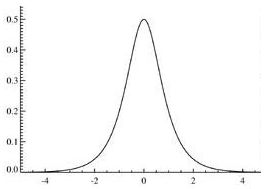La difficulté de réalisation réside dans le contrôle des caractéristiques de chaque impulsion, nécessairement de forme sécante hyperbolique.

Pour mémoire, nous rappelons l’expression de la fonction sécante hyperbolique ainsi que le graphe de cette fonction : \[\rm{sech}(x)=\frac{1}{\cosh(x)}=\frac{2}{\exp(x)+exp(-x)}\]

La source doit être capable d’émettre ce type d’impulsion :

• Longueur d’onde de \(1550\times 10^{-9}~m\)

• Largeurs temporelles à mi-hauteur de 20 à 40 \(\times 10^{-12}\) s

• Taux de répétition supérieurs à 5 Gb s\(^{-1}\)

• Puissances de crête de 5 mW

Disposer d’une source réunissant toutes ces caractéristiques de stabilité et de fiabilité compatible avec un usage industriel est un objectif ambitieux. Si l’on s’écarte de la forme idéale, l’impulsion se transformera au cours de sa propagation.

On définit sa largeur temporelles \(\Delta t\) et sa largeur spectrale \(\Delta f\). Une bonne forme d’impulsion est celle pour laquelle le produit \(\Delta t~\Delta f\) ne s’écarte pas trop de celle correspondante à la sécante hyperbolique : \[\Delta t~\Delta f=0,32\qquad[4]\]

5. Ressources bibliographique

1. A. Hasagawa

   Optical solitons in fibers (Spring Verlag, 1990)

2. J. Scott Russel

   Reports on the Meetings (British Association for the Advancement Science, 1884)

3. France Telecom

   Les communications optiques (Mémento technique, n° 4, 1994)

4. J.P. Hamaide, J. Chesnoy, J.M. Lourtioz

   Solitons optiques et télécommunications transocéaniques (Optique et imagerie)