1. Introduction

Les signaux rencontrés en physique subissent des transformations dans leur passage à travers un certain nombre de dispositifs. Ces transformations peuvent être utiles (détection, filtrage), mais aussi nuisibles (distorsions). Dans tous les cas, on peut représenter ces éléments comme des boîtes noires possédant une entrée et une sortie.

En télécommunications, une ligne de transmission peut être considérée comme un filtre. Il est donc utile d’étudier le comportement des filtres pour savoir comment se transforme un signal que l’on injecterait en entrée.

2. Filtre linéaire et invariant dans le temps (FLIT)

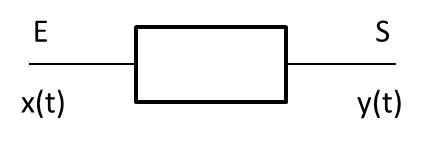Le signal sortant \(y(t)\) est la réponse au signal action ou entrant \(x(t)\). La linéarité se traduit mathématiquement par : \[a_1x_1(t)+a_2x_2(t) \ \ \rightarrow \ \ a_1y_1(t)+a_2y_2(t)\]

L’invariance dans le temps se traduit par : \[x(t-t_0) \ \ \rightarrow \ \ y(t-t_0)\]

La dernière relation s’interprète comme le fait que si le signal \(x(t\)) est retardé de \(t_0\) la réponse \(y(t)\) ne subit qu’un retard identique, sa forme étant conservée.

3. Réponse impulsionnelle. Fonction de transfert

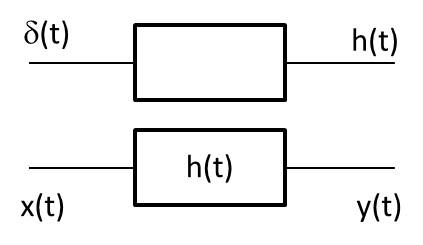Si le signal entrant est une impulsion de Dirac \(\delta(t)\), sa réponse impulsionnelle, parfois dite percusionnelle, est \(h(t)\).

\(L\) étant un opérateur linéaire, on peut écrire que : \[h(t)=L\{\delta(t)\}\]

En assimilant le signal continu \(x(t)\) à un train d’impulsions infiniment serrées modulées par l’amplitude de ce signal, on écrit que : \[x(t)=\int_{-\infty}^{+\infty}x(\tau)~\delta(t-\tau)~dt\]

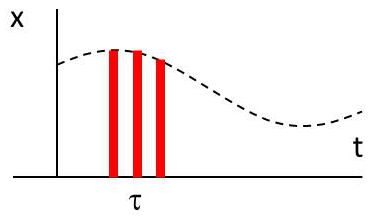Les opérateurs \(L\) et \(\int\) étant linéaires et permutables :

\[\begin{aligned} y(t)&=L\{x(t)\}=\int_{-\infty}^{+\infty}x(\tau)~L\{\delta(t-\tau)\}~d\tau \\ y(t)&=\int_{-\infty}^{+\infty}x(\tau)~h(t-\tau)\}~d\tau\end{aligned}\]

Le résultat est mathématiquement remarquable : c’est l’expression du produit de convolution entre le signal d’entrée \(x(t)\) et la réponse impulsionnelle \(h(t)\). On peut donc dire, ce qui s’entend parfois que le filtre est un convolueur : \[y(t)=x(t)\star h(t)\]

Compte tenu de la relation produit -– convolution connue sous le nom de théorème de Plancherel, on pourra écrire que : \[Y(f)=X(f)\times H(f)\]

Ainsi, dans l’espace des fréquences, le spectre de \(y(t)\) est le produit des spectres de \(x(t)\) et \(h(t)\). Une caractéristique remarquable du filtre a été mise en évidence, la fonction de transfert : \[H(f)=TF\{h(t)\} \qquad H(f)\in \mathbb{C}\]

On posera : \[H(f)=|H(f)|~e^{j\phi f}\] \[|H(f)| \qquad\qquad\qquad \text{gain de} H(f)~~~~\] \[\phi(f)=Arg[H(f)] \quad \text{phase de} H(f)\]

3.1. Réponse impulsionnelle réelle

Dans le cas de la réponse impulsionnelle réelle, le signal \(x(t)\) étant donné :

\[\begin{aligned} x(t) &= A\cos(2\pi f_0t)\\ x(t) &= \frac{A}{2}\left\{\int_{-\infty}^{+\infty}e^{j2\pi f_0t} + e^{-j2\pi f_0t}\right\} \qquad A \in \mathbb{R}\end{aligned}\]

D’où l’expression du produit de convolution : \[y(t)=\frac{A}{2}\left\{\int_{-\infty}^{+\infty}h(\tau)~e^{j2\pi f_0(t-\tau)}~d\tau + \int_{-\infty}^{+\infty}h(\tau)~e^{-j2\pi f_0(t-\tau)}~d\tau\right\}\]

Que l’on peut mettre sous la forme : \[y(t)= \frac{A}{2}\left\{e^{j2\pi f_0t}\int_{-\infty}^{+\infty}h(\tau)~e^{-j2\pi f_0t}~d\tau + e^{-j2\pi f_0t}\int_{-\infty}^{+\infty}h(\tau)~e^{+j2\pi f_0t}~d\tau \right\}\]

C’est-à-dire : \[y(t)=\frac{A}{2}\left\{H(f_0)~e^{j2\pi f_0t}+\overline{H(f_0)}~e^{-j2\pi f_0t}\right\}\]

Et finalement : \[y(t)=A~|H(f_0)|~\cos\big\{2\pi f_0t+Arg[H(f_0)]\big\}\]

Un filtre linéaire réel transforme une sinusoïde à la fréquence \(f_0\) en une nouvelle sinusoïde à la même fréquence avec un déphasage \(Arg[H(f_0)]\), l’amplitude étant par ailleurs multipliée par un facteur \(|H(f_0)|\).

4. Causalité

La notion de causalité semblera triviale, mais elle doit être prise en considération pour des raisons dont la logique sera perçue plus tard: : il ne doit pas y avoir de réponse en absence d’action. La condition de causalité s’énonce : La réponse ne doit pas précéder l’excitation.

Un filtre est physiquement réalisable s’il est causal et si sa réponse impulsionnelle est réelle. \[h(t)=0 \qquad t<0\]

Pour le signal de sortie : \[y(t)=x(t)\star h(t)=\int_{-\infty}^{+\infty}x(\tau)~h(t-\tau)~d\tau =\int_{-\infty}^t x(\tau)~h(t-\tau)~d\tau\]

Car : \[h(t-\tau)=0 \quad \text{quand} \ t-\tau<0 \quad \text{soit quand} \ \tau>t\]

La connaissance du signal de sortie à l’instant \(t\) ne nécessite pas la connaissance du signal d’entrée jusqu’à cet instant.

5. Stabilité

Un système est stable si et seulement si à toute entrée \(x(t)\) bornée \((M)\) correspond une sortie \(y(t)\) bornée \((M')\).

Le critère de stabilité s’énonce ainsi : La condition nécessaire et suffisante pour qu’un filtre linéaire soit stable est que : \[\int_{-\infty}^{+\infty}|h(t)|~dt~<\infty\]

Première conséquence : \[h(t)\rightarrow 0 \quad \text{quand}\quad t\rightarrow +\infty\]

6. Distorsion

On a vu que, dans le cas d’une entrée sinusoïdale, l’amplitude et la phase étaient altérées par transformation dans un filtre linéaire ; cette transformation peut être désirée dans des applications de traitement de signal, mais elle apparaît nuisible dans des applications de transmission : on l’appelle alors distorsion.

Un système est dit sans distorsion si : \[y(t)=A~x(t-t_0)\] \(A\) et \(t_0\) sont des constantes ;
\(t_0\) est le retard apporté par le filtre (temps de traversée) ;
\(A\) est le facteur de gain ou d’atténuation.

Un filtre linéaire est dit sans distorsion si la fonction de transfert peut s’écrire :

\[\begin{aligned} H(f)&=Ae^{-j2\pi ft_0 }\\ Y(f)&=H(f)~X(f)=A.e^{-j2\pi ft_0}~X(f)\\ y(t)&=A~x(t-t_0)\end{aligned}\]

Dans ce cas :
- le gain en fréquence est constant : \(|H(f)=A|\) ;
- le déphasage est une fonction linéaire de la fréquence : \(\phi(f)=-j2\pi ft_0\).

On distingue deux types de distorsions qui déforment le signal de sortie (phénomène d’écho) :
1) la distorsion d’amplitude : toutes les fréquences ne sont pas uniformément atténuées ou amplifiées ;
2) la distorsion de phase : toutes les fréquences ne sont pas uniformément retardées.

On notera qu’en vertu de la relation \(Y(f)=H(f)~X(f)\), on ne peut avoir en sortie de filtre d’autres fréquences que celles introduites à l’entrée.

7. Les filtres idéaux

On distingue plusieurs types de filtres idéaux, avec leur fonction de transfert \(H(f)\) comme une fonction rectangulaire. Il seront de plus supposés sans distorsion, c’est-à-dire avec une fonction de transfert \(H(f)\) constante et une phase linéaire dans la partie dite passante des fréquences.

7.1. Filtre passe-bas idéal

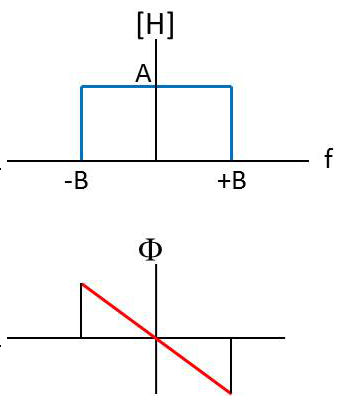Le filtre passe-bas est caractérisé par la fonction de transfert suivante (symétrique dans l’échelle des fréquences positives et négatives) :

\[\begin{aligned} |H(f)|&=A \qquad\qquad\quad |f|<B\\ \phi(f)&=-j2\pi ft_0 \qquad |f|<B\\ H(f)&=0 \qquad\qquad\quad \text{ ailleurs}\end{aligned}\]

B est la bande passante du filtre : \[H(f)=A~\Pi_{2B}(f)~e^{-j2\pi ft_0}\]

Dans la mesure où leur support en fréquences se situe dans la bande passante du filtre, les signaux d’entrée \(x(t)\) se retrouvent en sortie sans distorsion avec un simple retard \(t_0\).

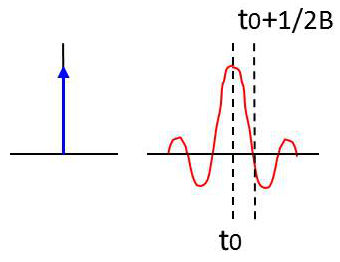
Examinons un exemple dans lequel le signal d’entrée \(x(t)\) a un spectre \(X(f)\) qui n’est pas contenu entièrement dans la bande du filtre. C’est le cas de l’impulsion \(x(t)=\delta(t)\) dont le spectre en fréquence (transformée de Fourier) est \(X(f)=1\), donc uniformément réparti sur toute l’échelle des fréquences.

On sait par ailleurs que le signal de sortie correspond à la réponse impulsionnelle \(y(t)=h(t)\).

En retenant la transformée de Fourier inverse : \[\Pi_{2B}(f) \ \ \rightarrow \ \ 2B~\frac{\sin 2\pi Bt}{2\pi Bt}=\sin c(2\pi Bt)\]

Il s’agit bien de la notation sinus cardinal.

Il vient pour le signal de sortie : \[y(t)=h(t)=TF^{-1}[H(f)]=2AB~\sin c[2\pi B(t-t_0)]\]

On remarque que l’impulsion émise en entrée ressort déformée et ce d’autant plus que la bande passante B est petite.

Si la bande passante \(B\) du filtre devient plus grande, c’est-à-dire \(B\rightarrow \infty\), alors le filtre passe-bas devient un filtre passe–tout et on retrouve intégralement en sortie l’impulsion émise en entrée.

7.2. Filtre passe-bande idéal

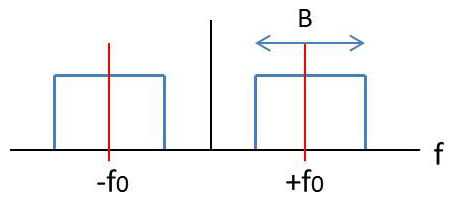Pour un filtre passe-bande, le module de la fonction de transfert est représenté par deux bandes de largeur \(B\) situées respectivement et symétriquement dans les parties positive et négative de l’échelle des fréquences : \[H(f)=A~\big\{\Pi_B(f-f_0)+\Pi_B(f+f_0)\big\}~e^{-j2\pi ft_0}\]

7.3. Filtre passe-haut idéal

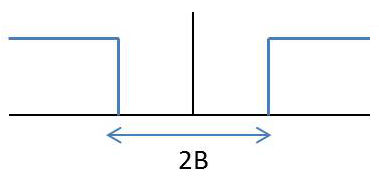Le filtre passe-haut apparaît comme le complémentaire du filtre passe-bas (fonction porte centrée sur l’origine des fréquences : \[H(f)=A~\big\{1-\Pi_{2B}\big\}~e^{-j2\pi ft_0}\]

8. Filtres réels

Si l’on calcule la réponse impulsionnelle des filtres idéaux (gain de transfert rectangulaire), on obtient des fonctions nulles pour \(t < 0\). Ces filtres, très utiles en pratique, sont donc physiquement irréalisables. On ne peut réaliser physiquement de filtres à coupure raide pour les fréquences situées immédiatement après la bande passante.

De nombreuses relations de filtres réalisables ont été envisagées pour approcher des filtres idéaux : certains sont dits de type polynomial, d’autres à pointes d’atténuation infinie. Il s’agit, grâce à une approximation mathématique, de trouver une expression de la fonction de transfert qui se rapproche au mieux de la forme idéale.

Toutes ces questions feront l’objet d’un chapitre particulier de traitement de signal réservé à l’analyse et la synthèse des filtres électroniques. Nous pouvons néanmoins donner un aperçu de ces approximations.

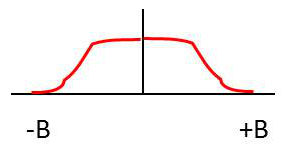Les approximations de type polynomial conduisent à des formes de \(|H(f)|\) semblables à celle représentée sur la figure ci-contre. Certaines ont une forme plus ou moins plate dans la bande passante (Butterworth, Besse, Papoulis ou Legendre), d’autres ont une ondulation plus ou moins serrée de part et d’autre du segment théorique de bande passante (en fonction de l’ordre du filtre).

La fonction de transfert est de la forme : \[H(p)=\frac{cte}{Q_n(p)}\]

\(Q_n(p)\) est un polynôme de degré \(n\) de la variable de Laplace \(p=j\omega\).

Les autres approximations correspondent à une fonction de transfert de la forme : \[H(p)=\frac{P(p)}{Q(p)} \qquad \text{ avec degré de } P < \text{degré de } Q\]

Ce qui revient à dire qu’il y a deux ondulations : l’une en bande passante, l’autre hors bande passante. On parle de zéros en bande passante et de zéros hors bande passante en fonction des pôles pour lesquels l’atténuation (logarithme de \(|H|\)) est naturellement infinie. C’est la raison pour laquelle on dit qu’il s’agit de filtres à pointes d’atténuation infinie, catégorie dans laquelle entrent les filtres de Zolotarev et les filtres de Cauer.