1. Dispositif à transfert de charges (CCD)
Principe du transfert
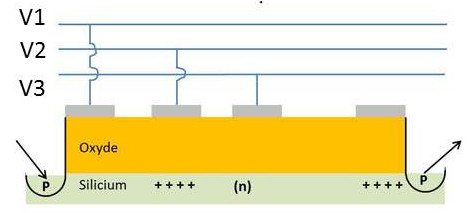Le dispositif à transfert de charges ou CCD (Charges Coupled Devices) est un cristal de silicium qu’une mince couche d’oxyde isole d’une électrode métallique.
La division de l’électrode en plusieurs sections permet de briser le flux continu des charges en plusieurs paquets et de bloquer leur mouvement que lorsque l’on change les tensions (période \(T\)) appliquées aux diverses section de l’électrode. On contrôle ainsi la vitesse de déplacement des charges ainsi que leur débit.
Équation de transfert
Considérons deux cellules (électrodes) consécutives repérées par leurs indices \(N\) et \(N+1\). Examinons l’état de ces cellules à l’instant \(t-1\) et à l’instant \(t\) (on a posé pour simplifier \(T~=~1\)).
À chaque temps d’horloge \(T\), les charges passent d’une électrode à l’autre mais une fraction \(\varepsilon\) est retenue (on suppose que \(\varepsilon\) est le même pour chaque cellule).
L’équation de transfert des charges peut s’écrire : \[q(n+1,t)=\varepsilon~q(n+1,t-1)+(1-\varepsilon)~q(n,t-1)\]
On applique la transformation en \(Z\) (système analogique échantillonné) : \[Q(n+1,z)=z^{-1}~\{\varepsilon~Q(n+1,z)+(1-\varepsilon)~Q(n,z)\}\]
On a donc : \[\frac{Q(n+1,z)}{Q(n,z)}=\frac{(1-\varepsilon)~z^{-1}}{1-\varepsilon~z^{-1}}\]
Dans un grand nombre d’applications, le coefficient de perte de charges est négligeable. On a alors : \[\frac{Q(n+1,z)}{Q(n,z)}=z^{-1} \quad ; \quad \frac{Q(N,z)}{Q(0,z)}=z^{-N}\]
\(N\) étant le nombre total de cellules, le dispositif est équivalent à une ligne à retard dont la fonction de transfert en \(z\), sous forme générale est : \[H(z)=\frac{V_s}{V_e}=\gamma~\frac{Q(N,z)}{Q(0,z)}=\gamma~z^{-N}\]
\(\gamma\) est un coefficient qui tient compte globalement des conductances et des capacitances à l’entrée et à la sortie du système.
CCD en filtre
La ligne à retard précédente peut être transformée en filtre en utilisant séparément les éléments de retard au moyen d’amplificateurs intégrés au CCD. On obtient alors un filtre de type récursif recevant des signaux échantillonnés non codés.
On applique pour cela une technique de transduction : le signal électrique est converti en charges électriques qui peuvent alors être transférées.
2. Dispositif à capacités commutées
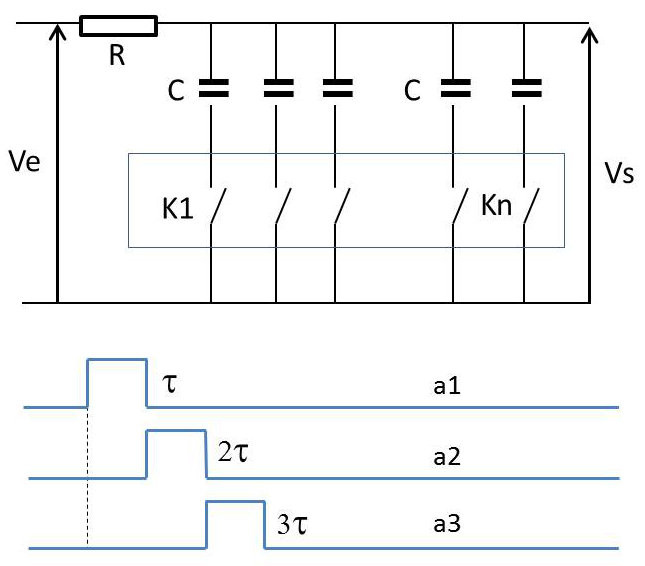Un filtre sélectif à capacités commutées est un filtre dont la fréquence de résonance est programmable par une horloge. Cette fréquence est rigoureusement stable, quelles que soient les conditions de fonctionnement du filtre.
Les interrupteurs \(K_i,~i=1,~2,~..,~n\) sont fermés en séquentiel pendant un laps de temps \(\tau\). La période \(T_0\) est le temps au bout duquel un interrupteur se retrouve fermé. La fréquence de résonance du filtre correspond à la fréquence de commutation des interrupteurs \(K_i\).
Si la fréquence de résonance \(F\) du signal d’entrée est un multiple de \(F_0\) (ou \(F_0\) elle-même), chaque capacité intègrera le signal d’entrée pendant le temps \(\tau\) de fermeture de l’interrupteur précédent.
S’il n’en est pas ainsi, l’amplitude du signal est considérablement affaiblie. En effet, si on suppose pour fixer les idées que \(F=F_0/2\), chaque capacité est chargée alternativement en positif ou en négatif de sorte que sa charge moyenne est nulle d’où l’affaiblissement de la tension de sortie \(V_s\).
Fonction de transfert du filtre
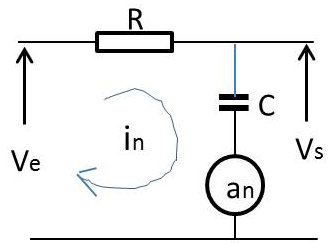Si \(a_n(t)\) représente l’expression temporelle de la fonction interrupteur \(K_n\), on peut écrire :
\[\begin{aligned} &i_n~=~a_n~\frac{V_e-u_n}{R}\\ &u_n~=~\frac{1}{C}\int_0^t i_n~dt\\ &v_s~=~\sum_{n=1}^Na_n~u_n\end{aligned}\]
En appliquant la transformation de Fourier :
\[\begin{aligned} &I_n=A_n\star\frac{V_e-U_n}{R}\\ &U_n=\frac{1}{j2\pi fC}~I_n\\ &V_s=\sum_{n=1}^N A_n\star U_n\end{aligned}\]
Le spectre en fréquence de l’interrupteur (fonction porte) est une forme de diffraction en sinus cardinal ou \(\sin x/x\). Si on limite le spectre du signal d’entrée (signal sinusoïdal pur), on a alors une fonction de transfert : \[H(f)=\frac{V_s(f)}{V_e(f)}=\sum_{k=-\infty}^{\infty}\frac{\sin k\pi/N}{k\pi/N}\cdot\frac{1}{1+j2\pi(f-kF_0)~NRC}\]
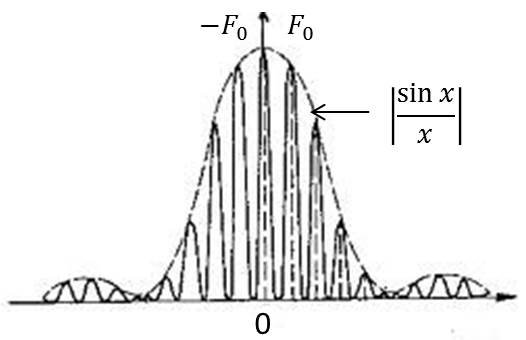La réponse harmonique \(|H(f)|\) est une somme de réponses harmoniques de filtres passe-bas du premier ordre (fréquence de coupure \(F_0=1/2\pi NRC\)), mais translatées de \(kF_0\) et pondérées par \(\sin x/x\), avec \(x=k\pi/N\).
En définitive, on retrouve un filtre passe-bas pour \(k=0\) et des filtres sélectifs passe-bande centrés sur \(F_0\), \(2 F_0\), ..., \(kF_0\) avec les caractéristiques suivantes :
\[\begin{aligned} &&&B=\frac{1}{\pi NRC} &&\text{bande passante}\\ &&&Q_n=\frac{nF_0}{B}=\pi NRC~nF_0 &&\text{surtension}&&\end{aligned}\]
