1. Description

L’étude des transistors unipolaires étant plus simple que celles des transistors bipolaires en raison de leur grande résistance d’entrée, nous avons choisi un amplificateur à deux étages TEC pour décrire le principe de l’amplificateur classique.

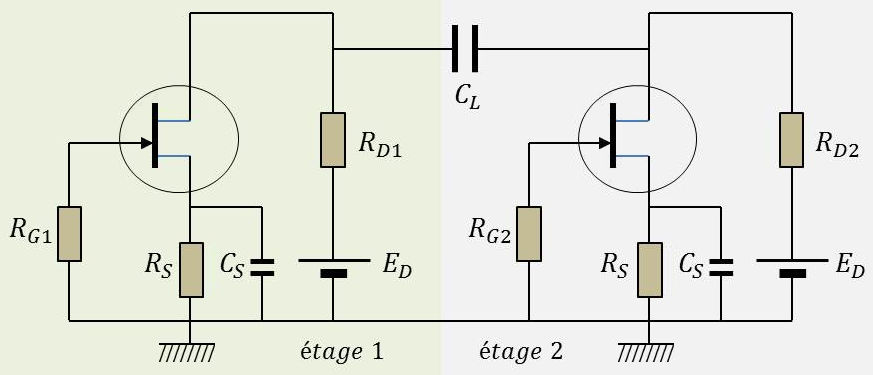Le filtre RC assure l’association des deux étages : un condensateur de liaison \(C_L\) et une résistance de fuites \(R_{G2}\).

Chaque étage fonctionne en classe A sans courant grille, la polarisation automatique des grilles étant assurée par les résistances de source \(R_S\) shuntées par des condensateurs polarisés.

À titre comparatif, nous pouvons considérer le schéma d’un ampli BF à deux étages dans une technologie bipolaire.

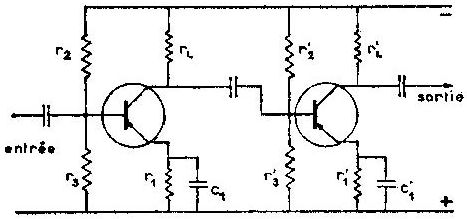Celui-ci est la transposition du montage à deux étage triodes. Il n’en diffère que par l’adjonction de deux résistances \(r_2\) et \(r'_2\)

Elles servent à stabiliser le gain contre les variations de température et en même temps à le rendre moins sensible au remplacement d’un transistor par un autre de caractéristiques légèrement différentes.

On appelle courbes de réponse d’un étage, les courbes qui représentent le gain et le déphasage en fonction de la fréquence.

Ces courbes sont faciles à obtenir expérimentalement avec le matériel usuel de laboratoire si l’amplificateur est observé en état de marche. Mais on peut également les déterminer par le calcul, à partir de l’utilisation des circuits équivalents.

2. Circuit équivalent

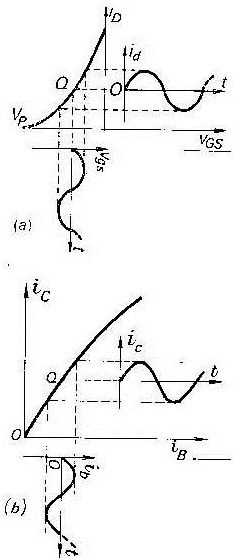Déterminons (expérimentalement) le point de repos \(Q\) (origine des courbes latérales fonctions du temps). On exprime sous forme mathématique la caractéristique : \[i_D=f(v_{GS})\quad\text{à}~~V_{DS}=\text{cte}\]

Son allure est parabolique : \[i_D=I_{D0}~\Big(1-\frac{V_{GS}}{V_P}\Big)^2\]

• \(I_{D0}\) : courant de drain pour \(v_{GS}=0\)

• \(V_P\) : tension de pincement

Par ailleurs, pour le régime variable, on tient compte :

• d’une part, des capacités parasites,

• d’autre part, des capacités de liaison (\(C_L\)) et de découplage (\(C_S\)).

Nous supposerons, pour simplifier, que le condensateur de source a une capacité très grande (infinie).

On appelle tension d’entrée la tension sinusoïdale appliquée entre la grille et la source du premier étage : \(v_1=v_{g1~s1}\).

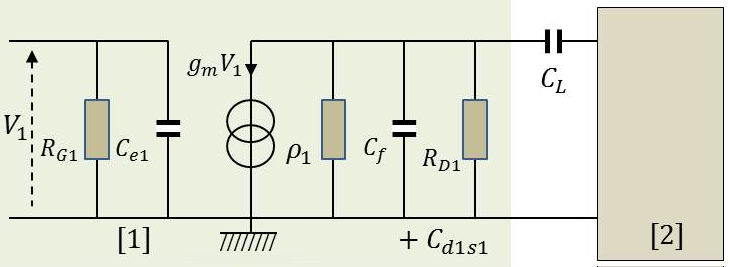La tension de sortie de cet étage est la tension d’entrée de l’étage suivant, c’est-à-dire : \(v_2=v_{g2~s2}\).

Noter que seule la partie centrale du circuit équivalent est nécessaire pour le calcul du gain du premier étage : \[\begin{aligned} &a~=~\frac{v_2}{v_1}\qquad\text{en notation instantanée}\\ &A~=~\frac{V_2}{V_1}\qquad\text{en notation complexe} \end{aligned}\]

2.1. Fréquences intermédiaires

Aux fréquences intermédiaires, les capacités du TEC et du fil de câblage (\(C_{d1s1},~C_{e2},~C_f\)), branchées en parallèle avec des résistances, peuvent être négligées quand leurs impédances sont grandes par rapport à ces résistances, ce qui a lieu pour des fréquences faibles. Le condensateur de liaison \(C_L\), en série avec la résistance de fuite \(R_{G2}\), est lui aussi négligeable aux fréquences élevées.

Il existe ainsi un domaine de fréquences à l’intérieur duquel toutes les capacités peuvent être supprimées. Dans cette bande intermédiaire de fréquence ou encore bande médiane, le gain a une valeur constante (\(a\)).

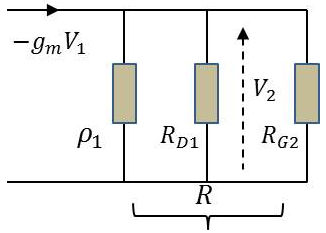On désigne par \(R\) la résistance équivalente aux trois résistances en parallèle. On a alors : \[V_2=-g_m~R~V_1\quad\Rightarrow\quad A_0=-g_m~R=-a_0\]

Pour les fréquences intermédiaires, les tensions d’entrée et de sortie d’un étage sont donc en opposition de phase.

2.2. Fréquences basses

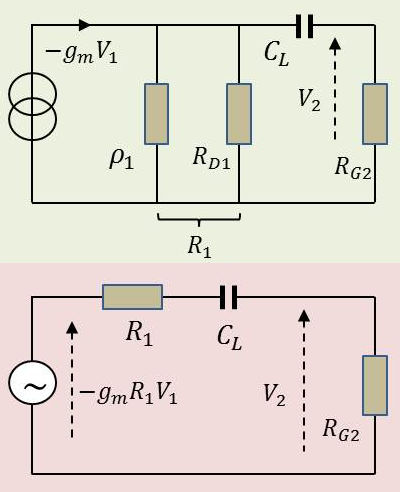Aux fréquences basses, comme pour les fréquences intermédiaires, on peut encore négliger les capacités parasites mais on doit tenir compte du condensateur de liaison \(C_L\).

Si l’on remplace les résistances \(\rho_1\) et \(R_{D1}\) par leur résistance équivalente \(R_1\), on peut alors substituer au générateur de courant un générateur de tension et l’on a : \[\frac{V_2}{-g_m~R_1~V_1}=\frac{R_{G2}}{R_1+R_{G2}-\cfrac{j}{C_L~\omega}}\]

Tous calculs faits : \[A=\frac{V_2}{V_1}=\frac{-g_m~R}{1-\cfrac{j}{(R_1+R_{G2})~C_L~\omega}}\]

Cette expression du gain permet de retrouver le gain aux fréquences intermédiaires dans le cas particulier suivant : \[\omega=\infty\quad\Rightarrow\quad A=-g_m~R\]

2.3. Fréquences élevées

Aux fréquences élevées, on peut négliger le condensateur de liaison, mais on doit tenir compte des capacités du TEC et du fil de câblage. Ces capacités, en parallèle, sont équivalentes à une capacité unique : \[C=C_{d1~s1}+C_{g2~s1}+C_{g2~d2}~(1+a_2)+C_f\]

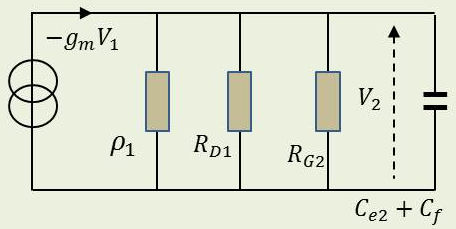Cette expression laisse apparaître une certaine indétermination puisque le gain \(a_2\) du deuxième étage est lui-même variable en fonction de la fréquence.

Dans la pratique, on ne commet qu’une faible erreur sur la capacité globale \(C\) en prenant pour \(a_2\) la valeur : \[a_2=g_mR_2\qquad\text{avec :}\quad R_2=\rho_2~//~R_{D2}\]

Elle correspond aux fréquences intermédiaires, puisque les trois autres capacités parasites sont connues avec précision.

Soit \(Z\) l’impédance équivalente aux résistances et aux capacités branchées en parallèle : \[\frac{1}{Z}=\frac{1}{R}+j~C~\omega\]

D’où : \[V_2=-g_m~Z~V_1=\frac{-g_m~R~V_1}{1+j~C~\omega}\]

Soit : \[A=\frac{-g_m~R}{1+j~R~C~\omega}\]

Avec cette expression du gain, on a bien comme cas particulier : \[A=-g_m~R=A_0\qquad\text{pour :}\quad\omega=0\]

ce qui correspond aux fréquences intermédiaires.

3. Courbes de réponse

3.1. Coordonnées réduites

On constate qu’un étage en audiofréquences se comporte comme un filtre passe-bande. Il laisse effectivement passer certaines fréquences avec un gain constant alors qu’il affaiblit les fréquences très basses et les fréquences très élevées.

Cet affaiblissement du gain s’accompagne d’une modification de la phase, ce qui nous conduit à représenter deux courbes distinctes : l’amplitude et la phase en fonction de la fréquence.

Le raisonnement est celui du circuit accordé, en coordonnées réduites. On traite séparément les domaines basses et hautes fréquences, puis on définit à l’intérieur de chacun de ces domaines les pulsations de coupure. Il s’agit des pulsations \(\omega_1\) et \(\omega_2\) qui provoquent une diminution de gain de 3 dB, c’est-à-dire, en module : \(a=a_0~/\sqrt{2}\).

Si l’on considère les relations obtenues pour chacun des deux domaines : \[A_1=\frac{A_0}{1+\cfrac{j}{(R_1+R_{G2})~C_L~\omega}}\quad;\quad A_2=\frac{A_0}{1+j~R~C~\omega}\]

On a : \[\omega_1=\frac{1}{(R_1+R_{G_2})~C_L}\quad;\quad \omega_2=\frac{1}{R~C}\]

Enfin, si l’on pose : \[Y=\frac{A}{A_0}\quad;\quad x_1=\frac{\omega}{\omega_1}=\frac{f}{f_1}\quad;\quad x_2=\frac{\omega}{\omega_2}=\frac{f}{f_2}\]

Il vient : \[Y_1=\frac{1}{1-j~x_1}\quad;\quad Y_2=\frac{1}{1+j~x_2}\]

3.2. Diagramme de Bode

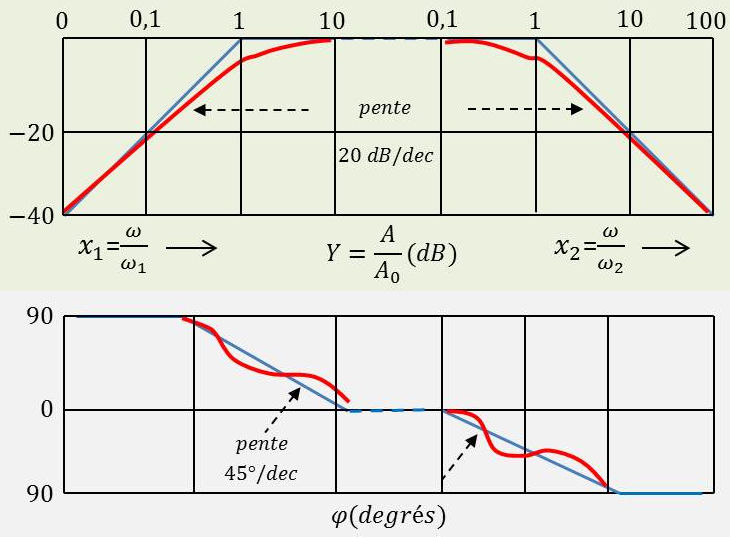On représente séparément les courbes d’amplitude et de phase en adoptant une graduation logarithmique pour l’axe des pulsations, l’amplitude et la phase étant respectivement exprimées en décibels et en degrés.

On détermine en premier lieu les asymptotes, puis on représente les courbes réelles en calculant le gain et la phase aux différentes fréquences de coupure.

Il est alors intéressant de remplacer la courbe réelle par une courbe idéalisée formée d’éléments linéaires. Pour cela, on peut assimiler les courbes à leurs asymptotes, représentation très satisfaisante pour l’amplitude, mais qui manque de précision pour la phase.

On obtient une meilleure allure de la courbe de phase en représentant le passage d’une asymptote à l’autre par un segment de droite dont les extrémités correspondent à une décade en dessous et une décade en dessus de la fréquence de coupure, la pente d’une telle droite étant de 45° par décade.

Noter que la fréquence de coupure correspond bien à une véritable cassure, c’est-à-dire à une brusque variation aussi bien de l’amplitude que de la phase.

Largeur de bande de l’étage exprimé en Hz : \[B=\Delta F=f_2-f_1\]

3.3. Remarque

L’étude précédente conduit à deux expressions différentes du gain, soit :

\[\begin{aligned} A_1&=-A_0~\frac{1}{1-j~\cfrac{\omega}{\omega_1}}\qquad\text{en BF}\\ A_2&=-A_0~\frac{1}{1+j~\cfrac{\omega}{\omega_2}}\qquad\text{en HF}\end{aligned}\]

Il est possible de grouper ces deux expressions en une réponse globale de l’étage : \[A=-\frac{A_0}{\Big(1-j~\cfrac{\omega_1}{\omega}\Big)\Big(1+j~\cfrac{\omega}{\omega_2}\Big)} =-A_0~\frac{j~\cfrac{\omega}{\omega_1}}{\Big(1+j~\cfrac{\omega}{\omega_1}\Big)\Big(1+j~\cfrac{\omega}{\omega_2}\Big)}\]

Avec :

\[\begin{aligned} &\omega\ll\omega_2\qquad\text{soit :}\quad\frac{\omega}{\omega_2}\ll 1\qquad\text{en BF}\\ &\omega\gg\omega_1\qquad\text{soit :}\quad\frac{\omega_1}{\omega}\gg 1\qquad\text{en HF}\end{aligned}\]

4. Facteur de mérite d’un TEC

Pour les amplificateurs à très large bande, on peut, sans grosse erreur, négliger \(\omega_1\) par rapport à \(\omega_2\), ce qui permet d’assimiler la bande passante de l’étage à la seule fréquence de coupure supérieure, soit : \[B\approx f_2=\frac{\omega_2}{2\pi}\]

Comme \(\omega_2=1~/~R~C\) et \(A_0=g_m~R\) : \[M=A_0~B=\frac{g_m}{2\pi~C}\]

Pour un TEC donné, le produit du gain par la largeur de bande est une constante qui ne dépend que des caractéristiques du TEC (pente et capacités parasites).

Plus cette constante est élevée, meilleures seront les performances du TEC. C’est pourquoi on l’appelle facteur de mérite du TEC.

Comme le gain n’a pas de dimension, ce facteur s’exprime dans les mêmes unités que la bande passante (Hz ou rd/s).