1. Origines du bruit de fond
Le bruit de fond des équipements électroniques est lié aux fluctuations spontanées qui affectent une grandeur électrique (tension, courant ou champ) dans les divers composants (actifs ou passifs) des circuits.
Ces fluctuations sont dues au caractère granulaire de la matière et en particulier au fait que les grandeurs précédentes dépendent des mouvements désordonnés de charges élémentaires. Ces charges sont généralement en très grand nombre et leur action globale nous apparaît comme constante ou continument variable. Toutefois, chaque particule étant animée d’un mouvement aléatoire, la grandeur électrique considérée fluctue également de manière aléatoire autour de sa valeur moyenne.
Ces fluctuations spontanées dans les composants sont des bruits d’origine interne qui constituent comme telles une limitation de base à la transmission de l’information sous forme électrique.
Les deux sources principales de bruit d’origine interne sont :
– le bruit thermique ou bruit Johnson qui apparaît dans les résistances au sens large du terme. Il est dû à l’agitation thermique des électrons dans les conducteurs et augmente donc avec la température ;
– le bruit de grenaille ou bruit Schottky qui apparaît dans les sources de courant électronique (diodes, transistors etc.). Il est dû à l’émission discrète des porteurs de charge et celle-ci s’accompagne inévitablement de fluctuations.
D’autres types de bruit existent. Contrairement aux bruits thermique et de grenaille, ces bruits dépendent de la fréquence.
Le plus important est le bruit de scintillation ou flicker effect. Il s’agit d’un bruit à variation lente, raison pour laquelle il prédomine en BF. D’où son appellation de bruit en 1/f. On l’attribue à des inhomogénéités dans la réalisation des composants. Relativement faible pour les transistors à jonctions, il devient négligeable pour les transistors à effet de champ qui ont subi moins d’opérations au cours de la fabrication. Ce type de bruit se manifeste également dans les résistances au carbone et les résistances à couche mince.
Parmi les autres types de bruit importants en BF, citons pour ce qui concerne les semi-conducteurs le bruit de générations-recombinaisons et le bruit en créneaux appelé encore burst noise ou popcorn noise.
Le premier est lié à des phénomènes de capture aléatoire sur des centres recombinants ainsi qu’à des phénomènes de régénération dans des bandes de conduction et de valence. Le deuxième est caractérisé par une instabilité du niveau moyen de signal qui affecte des transitions rapides d’un niveau à un autre. Il a été mis en évidence dans les diodes tunnel, les diodes à jonction, les transistors bipolaires et les circuits intégrés.
2. Caractérisation du bruit de fond
Le signal de bruit est essentiellement estimé par une puissance \(P_b\). Celui-ci se superpose à un signal utile. La dégradation du signal par le bruit est caractérisée par le rapport \(P_{signal}/P_{bruit}\), souvent noté S/N (signal over noise) ou SNR (signal to noise ratio).
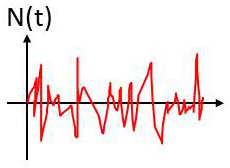Dans la représentation temporelle du phénomène (figure ci-contre), on s’intéresse aux variations spontanées de l’amplitude du bruit (courant ou tension). On s’en préoccupe particulièrement lors de l’étude des systèmes numériques, car les variations d’amplitude ont un effet déterminant sur le taux d’erreur des systèmes.
Dans l’aspect fréquentiel du phénomène (cas le plus fréquent), on introduit la densité spectrale de puissance de bruit \(W(f)\) à partir de la puissance de bruit traversant un filtre de fréquence caractérisé par une bande passante \(df\) infiniment étroite.
Pour un système de bande passante \([f_1,f_2]\) : \[dP_B=W(f)~df \quad \Rightarrow \quad P_B=\int_{f_1}^{f_2}W(f)~df\]
Bruit blanc
Le bruit blanc a une densité spectrale de puissance de bruit constante ou indépendante de la fréquence. Un tel bruit n’existe pas physiquement, car l’intégration sur une bande passante infinie conduirait à une puissance totale de bruit infinie. Cependant, très souvent, on peut considérer que le bruit est blanc sur une bande passante relativement large, à partir du moment où elle couvre totalement la bande passante du système considéré.
Bruit rose
Le bruit rose a une densité spectrale de puissance qui dépend de la fréquence. Un exemple typique est celui du bruit de scintillation dans les systèmes électroniques dont la densité spectrale varie en \(1/f\). En principe, ce bruit n’est important que pour les BF. Cependant, le registre BF peut être en fait relativement étendu, en fonction du type de composants utilisés. Pour les transistors bipolaires, ce type de bruit est limité à quelques kilo-hertz. Pour les transistors à effet de champ au silicium, il peut s’étendre jusqu’à quelques dizaines de kilohertz et pour les transistors à effet de champ à l’arséniure de gallium, il peut s’étendre jusqu’à quelques dizaines de mégahertz.
Nous noterons que cette représentation fréquentielle est très utilisée lorsque l’on étudie des systèmes analogiques.
3. Bruit d’un dipôle
3.1. Bruit thermique d’une résistance
Le bruit de fond d’une résistance – au sens large du terme – est un bruit d’origine thermique. Il se manifeste dans tout composant dont la caractéristique est à l’origine d’une dissipation d’énergie : résistance pure, résistance de perte d’un condensateur ou d’une bobine d’auto-induction, résistance de base d’un transistor à jonctions, résistance de rayonnement d’une antenne, etc.
D’un point de vue théorique, la thermodynamique statistique permet d’établir que les électrons – par leur agitation thermique dans un condensateur à la température absolue T – constituent un générateur de bruit de densité spectrale unilatérale de puissance :
\[\begin{aligned} &n(f)=\frac{h~f}{e~^{hf/kT-1}}\\ &f&&\text{fréquence en Hertz}\\ &h=6,62~.~10^{-34}~J.s&&\text{constante de Planck}\\ &k=1,38~.~10^{-23}J/^oK&&\text{constante de Boltzmann}\end{aligned}\]
Dans le domaine des fréquences radioélectriques : \[h~f \ll k~T \quad \Rightarrow \quad n(f)\approx k~T\]
La densité spectrale de puissance est alors indépendante de la fréquence : le bruit thermique est, dans ces conditions, un bruit blanc.
Remarquer que l’aspect quantique a disparu puisque la constante de Planck n’intervient plus. Par exemple, à la température \(t=20^oC\) (ou absolue \(T= 293^oK\)), on obtient une puissance \(P_B= k~T~\Delta f = 400~pW\) pour une bande de fréquence de largeur \(\Delta f=100~GHz\).
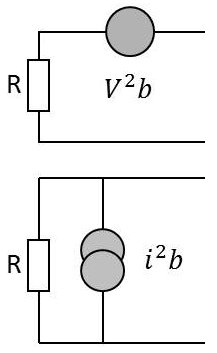On peut obtenir deux schémas équivalents de résistance bruitée en plaçant :
– soit une source de tension \(V^2_b\) en série avec la résistance (selon le théorème de Thévenin) ;
– soit une source de courant \(i^2_b\) en parallèle sur la résistance (selon le théorème de Norton).
La tension est donnée par la formule de Nyquist à établir.
On rappelle qu’un générateur de force électromotrice (fém) \(Eg\) et d’impédance interne \(Zg\) fournit à une charge \(Z_c\) une puissance maximale (puissance disponible du générateur) lorsque \(Z_c = Z_g\).
Dans le cas où \(Z_g = R_g\), on sait que cette puissance disponible a pour valeur : \[P=\frac{E^2_g}{4~R_g}\]
On détermine ainsi la fém de bruit dans une bande passante \(\Delta f\) sous forme quadratique moyenne en identifiant la puissance disponible de bruit \((k~T~\Delta f)\) à l’expression générale de la puissance disponible. L’expression précédente est alors remplacée par : \[P=\frac{\overline{e^2}}{4~R}\]
Il s’agit donc d’une valeur efficace, d’où la formule de Nyquist : \[V^2_{effB}=4k~T~R~\Delta f \quad \Rightarrow \quad \overline{V_B}=2\sqrt{k~T~R~\Delta f}\]
La valeur moyenne du bruit étant nulle, c’est à partir de la tension quadratique moyenne que l’on détermine la fém efficace de bruit grâce au voltmètre efficace vrai (dit encore RMS ou Root Mean Square).
Enfin, à partir de cette formule et en appliquant le théorème de Norton : \[I^2_{effB}=\frac{4k~R~T~\Delta f}{R}\]
Exemple : Un doublet demi-onde est utilisé pour capter un émetteur terrestre. La température au sol est \(20^oC\). La largeur de bande du récepteur vaut \(\Delta f=1~MHz\). La résistance de rayonnement du doublet est voisine de \(73~\Omega\). La valeur de la fém de bruit aux bornes de cette antenne est donc : \[2~\sqrt{1,38.10^{-23}~.~293~.~73~.~10^6}~\approx 1,1~\mu V\]
3.2. Bruit thermique d’un ensemble de résistances
3.2.1. Deux résistances en série
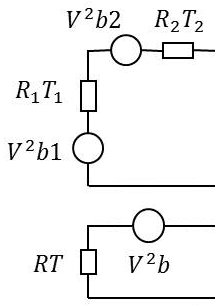Considérons deux résistances en série \(R_1\) et \(R_2\) placées respectivement aux températures \(T_1\) et \(T_2\). L’ensemble équivaut à un circuit comportant une résistance \(R\) et une source de tension \(V^2_b\) en série avec une résistance \(R=R_1+R_2\).
À chaque résistance bruitée correspond un processus aléatoire. Ces processus sont supposés non corrélés, ce qui autorise une addition des valeurs efficaces :
\[\begin{aligned} &V^2_b=(4k~T_1R_1+4k~T_2R_2)~\Delta f\\ &V^2_b=4k~(T_1R_1+T_2R_2)~\Delta f\end{aligned}\]
Tout se passe comme si l’ensemble était placé à une température équivalente \(T_{eq}\) telle que : \[V^2_b=4k~T_{eq}~R~\Delta f \quad ; \quad T_{eq}=\frac{R_1T_1+R_2T_2}{R_1+R_2}\]
3.2.2. Deux résistances en parallèle
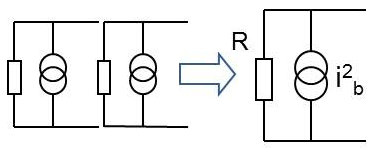On a cette fois : \[R=\frac{R_1R_2}{R_1+R_2}\]
Considérant comme précédemment que les deux processus aléatoires ne sont pas corrélés, on additionne les deux valeurs efficaces d’intensité : \[i^2_b=i^2_{b1}+i^2_{b2}=\left\{\frac{4k~T_1}{R_1}+\frac{4k~T_2}{R_2}\right\}\Delta f\]
On peut ici aussi définir une température équivalente de bruit telle que : \[i^2_b=\frac{4k~T_{eq}}{R}\Delta f \quad ; \quad T_{eq}=\frac{R_1T_2+R_2T_1}{R_1+R_2}\]
3.2.3. Circuit RC parallèle
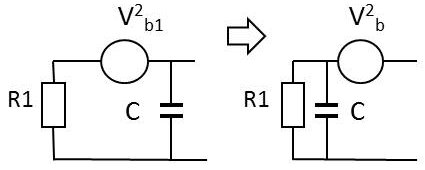Un circuit \(R_1C\) peut être mis sous la forme d’un circuit \(R_1C\) parallèle et d’une source de tension \(V^2_b\).
Le théorème de Thévenin permet de calculer celle-ci. C’est la tension qui apparaît aux bornes du circuit quand celui-ci est un circuit ouvert : \[V^2_b={\left|\frac{1}{jC\omega}\cdot\frac{1}{R+1/jC\omega}\right|}^2V^2_{b1}=\frac{4k~T~R_1}{1+R_1^2~C^2~\omega^2}~\Delta f\]
De la même façon, on peut calculer la source de tension de bruit à mettre en série avec n’importe quel dipôle passif. En appliquant le théorème de Norton, on peut aussi calculer la source de courant de bruit qu’il faut placer en parallèle sur tout dipôle.
3.3. Bruits dans les dipôles passifs
La théorie montre que le bruit thermique ne prend sa source que dans les résistances et que les réactances (inductances et capacités) réalisées de manière parfaite (inexistence de pertes ohmiques) ne produisent aucun bruit. Ainsi dans un dipôle passif, seules les résistances produisent du bruit. Pour un dipôle à température uniforme \(T\), la densité de puissance disponible est identique à celle d’une résistance pure \(N~=~k~T\).
On montre en fait que c’est la partie réelle de l’impédance du dipôle qui est source de bruit et que, en toute généralité, les densités de fém \(e\) ou de fcém \(j\) dépendent cette fois de la fréquence : \[{\overline{e~^2}}=4k~T~R_e~Z(f) \quad ; \quad \overline{j~^2}=4k~T~R_e~Y(f)\]
4. Bruit de grenaille
Le bruit de grenaille se manifeste essentiellement dans les composants électroniques où les porteurs de charge sont peu nombreux et circulent à des vitesses très grandes (tubes et semi-conducteurs).
À l’inverse, pour les conducteurs où les électrons sont beaucoup plus nombreux et les vitesses plus faibles (quelques mm/s pour des densités de courant de plusieurs A/mm²), le bruit de grenaille est négligeable devant le bruit d’origine thermique.
4.1. Diode à vide saturée
Quand une diode à vide est saturée, la tension d’anode est suffisante pour que tous les électrons émis par la cathode atteignent la plaque. Cette diode est équivalente à un générateur de courant : \[I(t)=I_S+i(t)\] \(I_S\) est le courant continu de saturation.
\(i(t)\) est un courant aléatoire de moyenne nulle et dont la valeur quadratique moyenne est donnée par la formule de Schottky : \[\overline{i^2}=2q~I_S~\Delta f\] \(q = 1,6.10^{-19}\) coulomb est la charge de l’électron.
\(\Delta f\) est la bande d’analyse du système de mesures.
Le bruit de grenaille est donc un bruit blanc. Cette approche constitue une très bonne approximation et reste valable jusqu’à des fréquences très élevées (voire supérieures au gigahertz pour un tube de distance inter-électrodes de 3 mm avec une tension appliquée de 300 volts.
4.2. Diode à jonction polarisée en direct
Pour une diode à jonction polarisée en direct, on obtient une relation de la même forme que précédemmentiode à jonction polarisée en direct : \[I(t)=I_d+i(t)\]
\(I_d\) est le courant de conduction direct : \[I_d=I_s~\exp\Bigl(\frac{q~V_d}{k~T}\Bigr)\] \(I_s\) : courant de saturation inverse
\(V_d\) : tension de polarisation directe
Le courant \(i(t)\) admet comme valeur quadratique moyenne : \[\overline{i^2}=2q~I_d~\Delta f\]
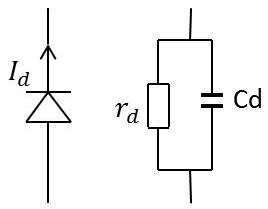
En régime de petits signaux, la diode à jonction est équivalente au schéma ci-contre :
\[\begin{aligned} &r_d=\frac{k~T}{q~I_d} &&\text{Résistance différentielle}\\ &C_d && \text{Capacité de diffusion}\end{aligned}\]
Densité de courant de bruit : \[\overline{i^2}=2q~I_d=2k~T_{g_d} \quad ; \quad g_d=\frac{1}{r_d}\]
La puissance de bruit disponible aux bornes d’une diode à jonction polarisée en direct est donc la moitié de celle que produirait une résistance métallique de valeur identique à la résistance différentielle de la diode.
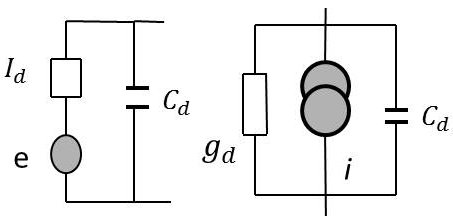On obtient alors les schémas équivalents de la diode avec bruit.
Pour les générateurs de tension et de courant : \[\overline{e^2}=2k~T~r_d \quad ; \quad \overline{i^2}=2k~T~g_d\]
Quelques ordres de grandeur :
\[\begin{aligned} &I_d=0,25~mA &&\sqrt{\overline{i^2}}=8,9~nA_{eff} && r_d=100~\Omega\\ &I_d=10~mA &&\sqrt{\overline{i^2}}=56,3~nA_{eff} && r_d=2,5~\Omega \end{aligned}\]
