1. Définitions

Les circuits linéaires sont constitués d’un ensemble de résistances, inductances et capacités, réelles ou mutuelles, connectées entre elles d’une manière quelconque.

Ces circuits sont passifs s’ils ne contiennent aucune source d’énergie électrique, de même qu’aucun élément transformant une énergie électrique en autre type d’énergie.

Un réseau linéaire contient un ou plusieurs générateurs de fréquences différentes.

La linéarité suppose que, pour chacun des éléments, la tension aux bornes \(v_n\) est une fonction linéaire de l’intensité \(i_n\) et de leurs dérivées ou intégrales par rapport au temps.

• Dipôle : réseau dont une paire de bornes particulières sont utilisées.

• Quadripôle : réseau dont deux paires particulières de bornes sont utilisées.

• Tripôle : quadripôle dont deux bornes sont en court-circuit.

2. Théorèmes sur les réseaux

2.1. Théorème de superposition

Énoncé

Le courant qui traverse une branche quelconque du réseau est la somme des courants que fournirait chacun des générateurs agissant isolément, les impédances internes des autres générateurs restant branchées et comptées comme telles dans le réseau.

2.2. Théorème de Thévenin

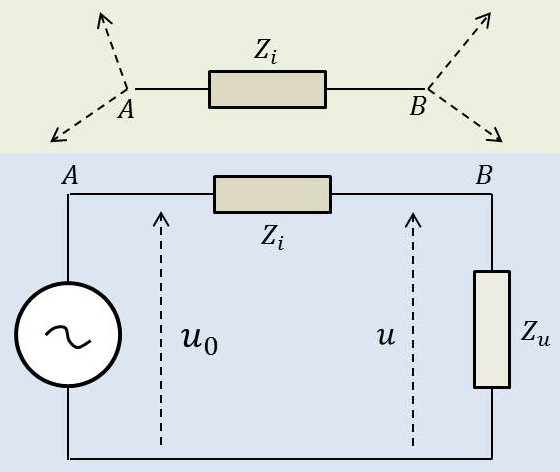
Nous voulons connaître le courant qui traverse l’une des branches AB du réseau. Cette branche va jouer le rôle d’un récepteur d’impédance \(Z_u\).

On effectue à présent deux opérations :

1. La branche AB étant enlevée, on calcule la tension qui apparaît entre les bornes A et B.

   Cette tension est, par définition, la f.é.m. du générateur de Thévenin.

2. La branche AB étant toujours enlevée, on court-circuite les f.é.m. de tous les générateurs tout en maintenant dans les différentes branches leurs impédances internes et on calcule l’impédance \(Z_i\) apparaissant entre les deux bornes A et B.

Cette impédance est l’impédance interne du générateur de Thévenin. Il est alors possible de substituer à l’ensemble du réseau un simple circuit à une seule branche. On en déduit l’expression l’intensité du courant qui alimente le récepteur soit : \[i=\frac{u_0}{Z_i+Z_u}\]

2.3. Théorème de Kennely

Le théorème de Kennely est encore connu comme la transformation dite étoile - triangle ou encore \(Y.\Delta\) et ceci, dans les deux sens.

2.3.1. Transformation triangle – étoile

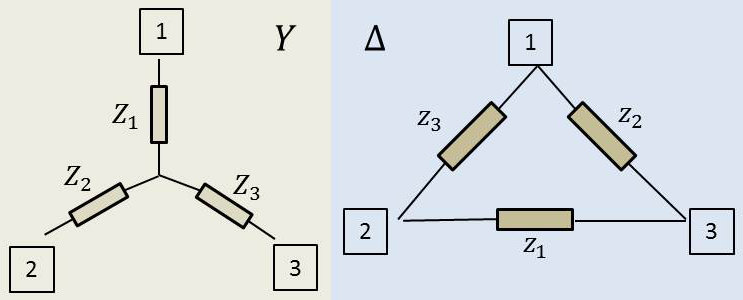Prenant à titre d’exemple ce qui est vu (et doit être conservé) en tant que impédance dans chacun des deux schémas entre les deux bornes [1] et [2] :

\[\begin{aligned} &Z_{12}=Z_1+Z_2\qquad\text{(schema 1)}\\ &\frac{1}{Z_{12}}=y_3+\frac{1}{z_1+z_2}\qquad\text{(schéma 2)}\\ &\frac{1}{Z_{12}}=\frac{y_1~y_2+y_2~y_3+y_3~y_1}{y_1+y_2}=\frac{\sum y_1~y_2}{y_1+y_2}\end{aligned}\]

En remarquant que \(Z_1\) est la branche de l’étoile reliée au point [1] alors que \(z_2\) et \(z_3\) sont les deux branches aboutissant à cette même borne, on obtient, tous calculs faits : \[Z_1=\frac{z_2~z_3}{z_1+z_2+z_3}\qquad\text{(et permutations)}\]

2.3.2. Transformation étoile - triangle

En raisonnant par dualité impédance – admittance, on obtient un résultat analogue : \[y_1=\frac{Y_2~Y_3}{Y_1+Y_2+Y_3}\qquad\text{(et permutations)}\]

2.4. Théorème de Norton

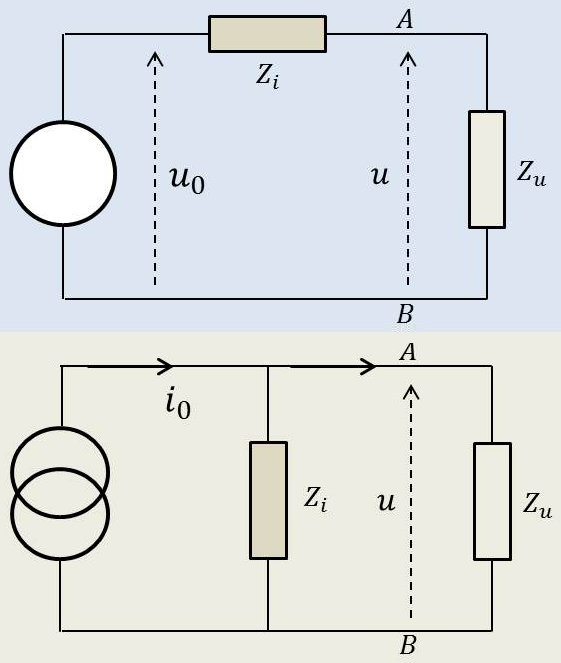Le théorème de Norton est encore connu comme celui de la transformation générateur courant \(\leftrightarrow\) tension. Dans les deux sens, comme pour le théorème précédent.

Il apparaît en fait comme une conséquence directe du théorème de Thévenin.

Considérons le premier circuit. Mettons en court-circuit les bornes de l’impédance de charge \(Z_u\). Le générateur voit alors \(Z_i\). Ou bien encore, le générateur de Thévenin débite un courant d’intensité : \[I_0=\frac{U_0}{Z_i}\]

Une remarque à faire, même triviale : ce courant est indépendant de la charge \(Z_u\).

Enlevons à présent le court-circuit. Le courant dans la charge reprend alors sa valeur d’origine : \[I=\frac{U_0}{Z_i+Z_u}=\frac{Z_i}{Z_i+Z_u}~I_0\]

Énoncé

On peut remplacer un générateur de tension \(U_0=cte\) – donc indépendante de la charge – par un générateur de courant \(I_0=cte\) – lui aussi indépendant de la charge – à condition de brancher l’impédance interne du générateur de Thévenin en parallèle avec la charge.

Remarque sur la dualité

Le passage du générateur de Thévenin au générateur de Norton est une conséquence du principe de dualité.

Un générateur de tension idéal a une impédance interne nulle. Un générateur de courant idéal a une admittance nulle (impédance interne infinie).

2.5. Théorème de réciprocité

Énoncé

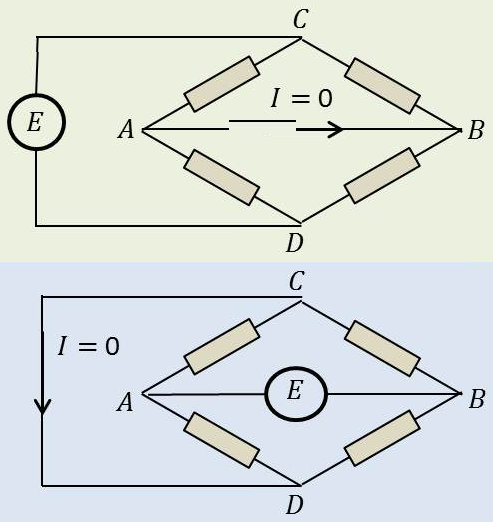
Si une f.é.m. \(E\) insérée dans une branche d’un réseau produit in courant \(I\) dans une autre branche, alors réciproquement cette f.é.m. \(E\) insérée dans cette deuxième branche produira le même courant \(I\) dans la première.

Application

Un exemple très simple est celui du pont équilibré :

Si le générateur de f.é.m. alternative E placé dans la branche AB produit un courant nul dans la branche CD, alors ce générateur, inséré maintenant dans la branche CD, produira un courant nul dans la branche AB.

2.6. Théorème de Millman

Énoncé

Dans un réseau électrique de branches parallèles, comprenant chacune un générateur de tension parfait avec un élément linéaire, la tension aux bornes des branches est égale à la somme des f.é.m. respectivement multipliées par l’admittance de la branche, le tout divisé par la somme des admittances.

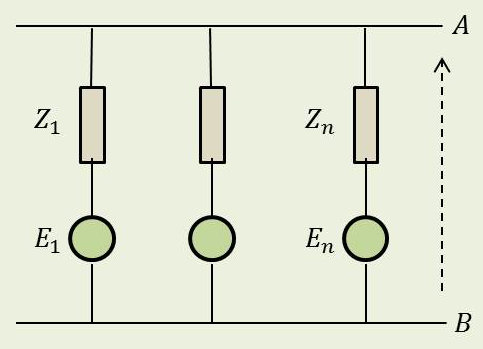Ce qui se traduit par la formule : \[U_{AB}=\frac{\sum E_k~Y_k}{\sum_{Y_k}}=\frac{\sum E_k/Z_k}{\sum 1/Z_k}\]

Remarques

1. Si une branche (k) ne contient pas de tension, on écrira pour cette branche : \(E_k=0\).

2. On doit d’autre part tenir compte du signe (\(\pm\)) de la tension de branche.

Application

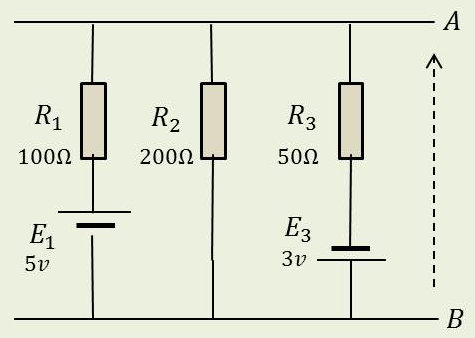On considère le circuit ci-contre, avec les deux particularités indiquées précédemment.

En appliquant directement la formule : \[U=\frac{5/100+0/200+(-3)/50}{1/100+1/200+1/50}\]

Ceci en ayant fait l’hypothèse du générateur idéal (résistance interne nulle).

3. Théorème de Foster

Énoncé

L’impédance d’un réseau dipôle passif purement réactif, donc ne contenant que des selfs, des mutuelles et des capacités, peut toujours se mettre sous la forme : \[Z=H~\frac{(\omega_1^2-\omega^2)~(\omega_2^2-\omega^2)~\dots~(\omega_n^2-\omega^2)}{j~\omega~(\omega_2^2-\omega^2)~\dots~(\omega_{2n-2}^2-\omega^2)}\]

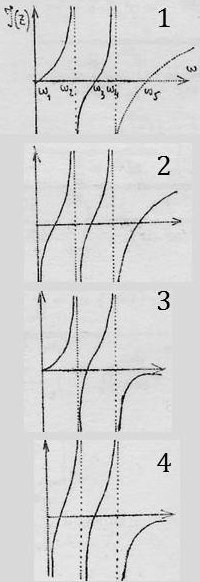\(H\) est une constante positive et par ailleurs  \[0\leq\omega_1\leq\omega_2\leq\omega_3\leq\dots\leq\omega_{2n-1}\leq\infty\]

Il en résulte que \(\mathcal{J}(Z)\) est une fonction toujours croissante de \(\omega\). Une représentation en est donnée ci-contre pour \(n=3\).

On met en évidence les quatre cas fondamentaux (notation : BF pour basse fréquence et HF pour haute fréquence) :

• Premier cas : selfique (BF et HF) \[\omega_1=0\quad;\quad\omega_5\neq\infty\]

• Deuxième cas : capacitif BF et selfique HF \[\omega_1\neq 0\quad;\quad\omega_5\neq\infty\]

• Troisième cas : selfique BF et capacitif HF \[\omega_1=0\quad;\quad\omega_5=\infty\]

• Quatrième cas : \[\omega_1\neq 0\quad;\quad\omega_5=\infty\]

Il faut noter également que si deux dipôles réactifs ont mêmes zéros et mêmes pôles, leurs impédances sont proportionnelles.

4. Calcul des courants

4.1. Méthode de Kirchhoff

On suppose le réseau alimenté par des tensions sinusoïdales de même fréquence.

Pour calculer les courants dans les différentes branches, on écrit que :

• \(\sum U=0\) pour les mailles (courants de boucle) ;

• \(\sum I=0\) , conservation des courants aux noeuds (loi d’Ohm).

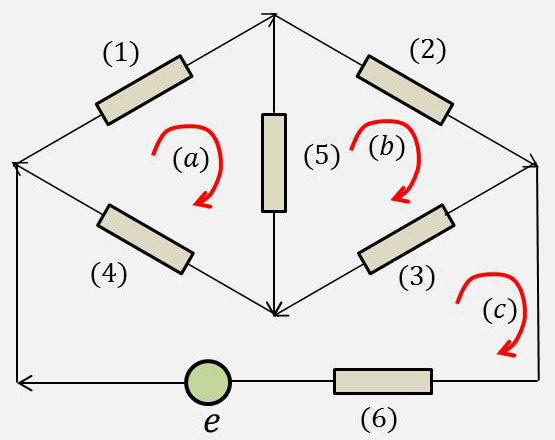Pour fixer les idées, prenons l’exemple du circuit ci-contre.

On exprime la conservation des courants aux noeuds du réseau (compte tenu des sens donnés à ces courants).

D’où les équations (indépendantes) : \[\left\{ \begin{aligned} &i_1-i_2-i_5=0\\ &i_2-i_3-i_6=0\\ &i_5+i_3-i_4=0 \end{aligned} \right.\]

On exprime la loi d’Ohm sur les boucles (indépendantes): \[\left\{ \begin{aligned} &z_1~i_1+z_5~i_5+z_4~i_4=0\\ &z_3~i_3+z_5~i_5+z_2~i_2=0\\ &z_3~i_3+z_6~i_6+z_4~i_4-e=0 \end{aligned} \right.\]

4.2. Méthode de Maxwell

La méthode de Maxwell est également connue sous le nom de méthode des mailles indépendantes. Elle est très voisine de la précédente mais en considérant cette fois des courants fictifs \(I\) dans les boucles indépendantes.

On choisit des sens arbitraires de courants dans les différentes mailles et on déduit facilement les courants dans les différentes branches. On obtient ainsi un premier système d’équations linéaires. Ce système est complété par un deuxième système, qui est cette fois l’expression de la loi d’Ohm dans les mêmes boucles.

Pour l’exemple précédemment, nous obtenons : \[\left\{ \begin{aligned} &i_1=I_a\\ &i_2=I_b\\ &i_3=I_b-I_c\\ &i_4=I_a-I_c\\ &i_5=I_a-I_b\\ &i_6=I_c \end{aligned} \right. \qquad\qquad\\ \left\{ \begin{aligned} &0=(z_1+z_4+z_5)~I_a-z_5~I_b-z_4~I_c\\ &0=(z_2+z_3+z_5)~I_b-z_3~I_c-z_5~I_a\\ &e=(z_6+z_4+z_3)~I_c-z_4~I_a-z_3~I_b \end{aligned} \right.\]