1. Convention de signes
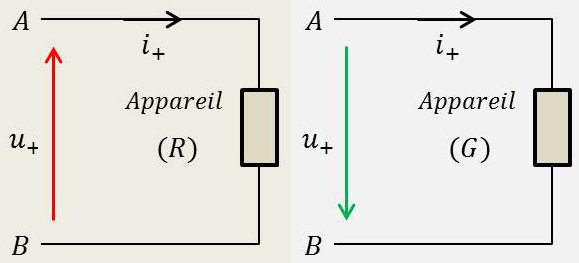Rappelons tout d’abord les conventions de signe de la loi d’Ohm. Figure ci-contre :
-
(R) : Système récepteur.
-
(G) : Système générateur.
2. Définition première du quadripôle
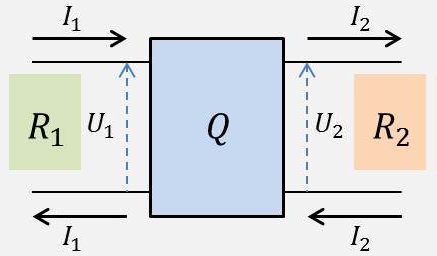Le quadripôle passif présente deux paires de bornes. Appelé parfois boîte noire, il intervient généralement comme un organe de liaison entre un réseau \(R_1\), relié à ses bornes d’entrée et un réseau \(R_2\) relié à ses bornes de sortie.
Cette configuration entrée et sortie montre intuitivement qu’au quadripôle Q peut être associée une représentation matricielle, c’est-à-dire des systèmes linéaires d’équations (entre tensions et courants).
3. Équations du quadripôle
Un quadripôle passif ne comporte que des éléments linéaires : résistances, capacités, inductances.
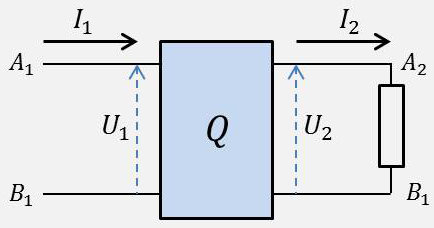On choisit des sens positifs pour les courants d’entrée \(I_1\) et de sortie \(I_2\). On adopte, pour l’entrée comme pour la sortie, les conventions du système récepteur. Les sens positifs des tensions d’entrée \(U_1\) et de sortie \(U_2\) sont définies de la même manière.
Quelle que soit sa complexité, le réseau est décomposé en mailles indépendantes. On peut calculer alors les courants des différentes mailles ce qui conduit à un système de n équations : \[\left\{ \begin{aligned} U_1&=z_{11}~I_1+z_{12}~I_2+\dots+z_{1n}~I_n\\ U_2&=z_{21}~I_1+z_{22}~I_2+\dots+z_{2n}~I_n\\ 0&=z_{31}~I_1+z_{32}~I_2+\dots+z_{3n}~I_n\\ &.~.~.~.~.~.~.~.~.\\ 0&=z_{n1}~I_1+z_{n2}~I_2+\dots+z_{nn}~I_n \end{aligned} \right. \qquad\Rightarrow\qquad \left\{ \begin{aligned} &U_1=Z_{11}~I_1+Z_{12}~I_2\\ &U_2=Z_{21}~I_1+Z_{22}~I_2 \end{aligned} \right.\]
Appliquons le théorème de réciprocité :
\[\begin{aligned} &U_2=0~,\text{ puis : }U_1=E\quad\Rightarrow\quad I_2=\frac{Z_{21}~E}{Z_{12}~Z_{21}-Z_{11}~Z_{22}}\\ &U_1=0~,\text{ puis : }U_2=E\quad\Rightarrow\quad I_2=\frac{Z_{12}~E}{Z_{21}~Z_{12}-Z_{22}~Z_{11}}\end{aligned}\]
Les dénominateurs étant identiques et les deux courants devant être égaux (réciprocité), on doit avoir : \[Z_{12}=Z_{21}\]
Le principe de dualité et l’application le théorème de réciprocité, conduira aux admittances : \[Y_{12}=Y_{21}\]
4. Signification physique des éléments
Chacun des paramètres \(Z_{ij}\) ou \(Y_{ij}\) a une signification physique. Pour la déterminer, il faut se placer dans des conditions particulières de fonctionnement auxquelles sont soumises les bornes d’entrée ou de sortie, à savoir en circuit ouvert ou court-circuit.
Le point de départ est le système d’équations : \[\left\{ \begin{aligned} &U_1=Z_{11}~I_1+Z_{12}~I_2\\ &U_2=Z_{21}~I_1+Z_{22}~I_2 \end{aligned} \right.\]
4.1. En impédances
Considérons plusieurs cas particuliers de fonctionnement :
-
Impédance d’entrée à vide
Impédance vue des bornes d’entrée, les bornes de sortie étant ouvertes : \[I_2=0\quad\Rightarrow\quad Z_{11}=\Big(\frac{U_1}{I_1}\Big)_{I_2=0}\]
-
Impédance de sortie à vide
Impédance vue des bornes de sortie, les bornes d’entrée étant ouvertes : \[I_1=0\quad\Rightarrow\quad Z_{22}=\Big(\frac{U_2}{I_2}\Big)_{I_1=0}\]
-
Impédance de couplage (ou impédance mutuelle) \[Z_{12}=Z_{21}\]
-
Identification avec une tension de sortie
Quand les bornes de sortie sont ouvertes : \[I_2=0\quad\Rightarrow\quad Z_{21}=\Big(\frac{U_2}{I_1}\Big)_{I_2=0}\]
-
Identification avec une tension d’entrée
Quand les bornes d’entrée sont ouvertes : \[I_1=0\quad\Rightarrow\quad Z_{12}=Z_{12}=\Big(\frac{U_1}{I_2}\Big)_{I_1=0}\]
4.2. En admittances
Symétriquement :
Admittance d’entrée de court-circuit : \[U_2=0\quad\Rightarrow\quad Y_{11}=\Big(\frac{I_1}{U_1}\Big)_{U_2=0}\]
Admittance de sortie de court-circuit : \[U_1=0\quad\Rightarrow\quad Y_{22}=\Big(\frac{I_2}{U_2}\Big)_{U_1=0}\]
Admittances de transfert : \[Y_{21}=\Big(\frac{I_2}{U_1}\Big)_{U_2=0}\quad\text{et}\quad Y_{12}=\Big(\frac{I_1}{U_2}\Big)_{U_1=0}\]
5. Circuits équivalents
Trois paramètres indépendants permettent donc de définir un quadripôle passif : \(Z_{11}\), \(Z_{22}\) et \(Z_{12}=Z_{21}\).
Deux structures de base permettent de construire un quadripôle :
-
la structure à trois éléments dite en \(T\) ;
-
la structure à trois éléments dite en \(\Pi\).
Il existe une certaine dualité du fait que :
-
la première correspond au branchement dit en étoile ;
-
la seconde correspond au branchement en dit en triangle.
5.1. Montage en T
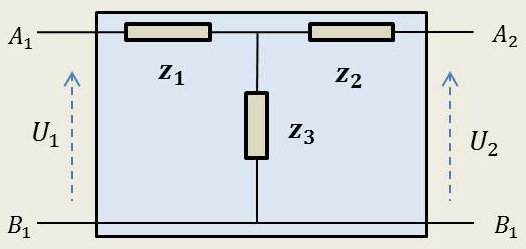On décompose le réseau d’un montage en T en deux mailles indépendantes. Le système d’équations permet de déterminer les éléments \(Z_{ij}\) : \[\left\{ \begin{aligned} &U_1=Z_{11}~I_1+Z_{12}~I_2\\ &U_2=Z_{21}~I_1+Z_{22}~I_2 \end{aligned} \right. \qquad \left\{ \begin{aligned} &Z_{11}=z_1+z_3\\ &Z_{22}=z_2+z_3\\ &Z_{12}=Z_{21}=z_3 \end{aligned} \right.\]
5.2. Montage en \(\Pi\)
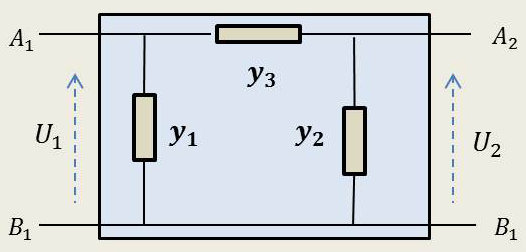Pour un montage en \(\Pi\), on procède par dualité : \[\left\{ \begin{aligned} &I_1=Z_{11}~U_1+Z_{12}~U_2\\ &I_2=Z_{21}~U_1+Z_{22}~U_2 \end{aligned} \right. \qquad \left\{ \begin{aligned} &Y_{11}=y_1+y_3\\ &Y_{22}=y_2+y_3\\ &Y_{12}=Y_{21}=y_3 \end{aligned} \right.\]
6. Impédance d’entrée d’un quadripôle
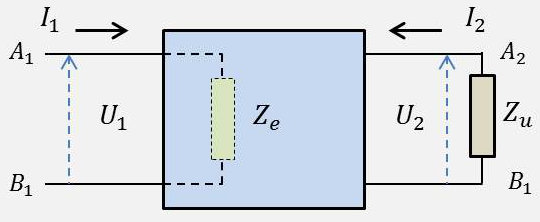Branchons aux bornes de sorties d’un quadripôle une impédance d’utilisation \(Z_u\). Vu des bornes d’entrée le quadripôle se comporte comme un dipôle d’impédance : \[Z_e=\frac{U_1}{I_1}\]
Il faut bien noter qu’il s’agit de l’impédance d’entrée du quadripôle (donc avec sa charge \(Z_u\)), à ne pas confondre avec l’impédance d’entrée à vide qui est \(Z_{11}\).
Compte tenu des conventions de signe (courants et tensions) :
\[\begin{aligned} &U_1=Z_{11}~I_1+Z_{12}~I_2\\ &U_2=Z_{21}~I_1+Z_{22}~I_2=-Z_u~I_2\end{aligned}\]
Et, tous calculs faits : \[Z_e=Z_{11}-\frac{Z_{12}^2}{Z_u+Z_{22}}\]
On peut remarquer cependant que si l’on fait \(Z_u=\infty\), on retrouve à cette limite \(Z_{11}\), c’est à dire l’impédance d’entrée à vide.
7. Adaptation d’impédance
L’adaptation d’impédance est un problème fondamental en électronique : étant donné un récepteur d’impédance \(Z_u\), on désire que ce récepteur reçoive la puissance maximale d’un système donné.
Par application du théorème de Thévenin, on peut remplacer le système qui alimente le récepteur par un générateur de f.é.m. \(U_0\) et d’impédance interne \(Z_i\). Dans la pratique, on peut considérer deux cas distincts : un cas particulier qui se présente très fréquemment et un cas général qui est peu courant.
7.1. Cas particulier
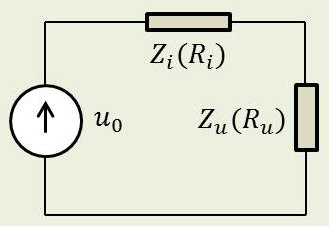En fait, le cas le plus fréquent est celui où le récepteur et le générateur de Thévenin sont des résistances pures.
Calculons la puissance active absorbée par le récepteur : \[P=R_u~I^2=\frac{R_u~U_0^2}{(R_u+R_i)^2}\]
On peut l’exprimer autrement : \[P=\frac{U_0^2}{(\sqrt{R_u}+\cfrac{R_i}{\sqrt{R_u}})^2}\]
Le dénominateur se présente comme le carré de la somme de deux termes dont le produit est constant. Sa valeur est donc maximale quand ces termes sont égaux, soit \(R_u=R_i\)
7.2. Cas général
Dans le cas général, le récepteur et le générateur de Thévenin sont des impédances quelconques : \[Z_i=R_i+j~X_i\qquad;\qquad Z_u=R_u+j~X_u\]
Les parties \(X_i,~X_u\) des impédances sont positives ou négatives suivant qu’il s’agit d’inductances ou de capacités.
La puissance active absorbée dans ce cas par le récepteur a pour expression : \[P=R_u~I^2=\frac{R_u~U_0^2}{(R_u+R_i)^2+(X_u+X_i)^2}\]
Cette puissance est d’autant plus élevée que le dénominateur est plus faible. Comme le dénominateur est la somme de deux termes, on a intérêt à annuler l’un des deux termes ; ceci n’est possible qu’en annulant (en théorie) l’un des deux termes. Or, seul le deuxième peut prendre une valeur nulle quand \(X_u=-X_i\).
Supposons cette condition satisfaite. On est alors ramené au cas précédent, ce qui impose comme deuxième condition \(R_u=R_i\).
Cette double condition peut s’exprimer sous la forme suivante :
Un récepteur reçoit la puissance maximale si son impédance est le conjugué de l’impédance du générateur de Thévenin qui l’alimente : \[Z_u=\overline{Z_i}\]
7.3. Remarque
Toute cette étude a fait apparaître une application très importante du quadripôle passif pouvant être considéré comme un adaptateur d’impédance.
Un récepteur doit recevoir la puissance maximale d’un générateur de Thévenin d’impédance interne \(Z_i\). En insérant un quadripôle entre le générateur et le récepteur, il est possible d’adapter l’impédance de la charge à la valeur convenable.
Les conditions d’adaptation s’expriment par : \[\overline{Z_i}=Z_e=Z_{11}-\frac{Z_{12}^2}{Z_u+Z_{22}}\]
