1. Une expérience historique

Henri Becquerel a découvert la radioactivité. Et son père Antoine Becquerel a été le premier à expérimenter les photopiles. Il appela son dispositif (montage métal - électrolyte - métal symétrique) pile photovoltaïque.

Il avait remarqué que s’il n’obtenait aucun potentiel dans l’obscurité, il pouvait déceler un courant quand l’une des électrodes était éclairée. En 1839, il publia un mémoire sur les effets électriques produits par l’influence des rayons solaires dans une pile constituée par des électrodes de platine et de cuivre oxydé plongeant dans une solution électrolytique acide.

Un principe était désormais acquis : il y a production d’électricité lorsqu’un éclairement convenable tombe sur la surface de séparation de deux milieux différents dont l’un au moins est un conducteur ionique (sels dissous ou fondus) ou un semi-conducteur. C’est le cas, par exemple, de lames d’or dans une solution d’acide chlorhydrique (conducteur ionique), ou d’oxyde cuivreux formé sur une lame de cuivre (semi-conducteur) dans de l’eau salée. On utilise aujourd’hui des semi-conducteurs type germanium ou silicium à rendement significatif.

2. Principe de fonctionnement de la pile solaire

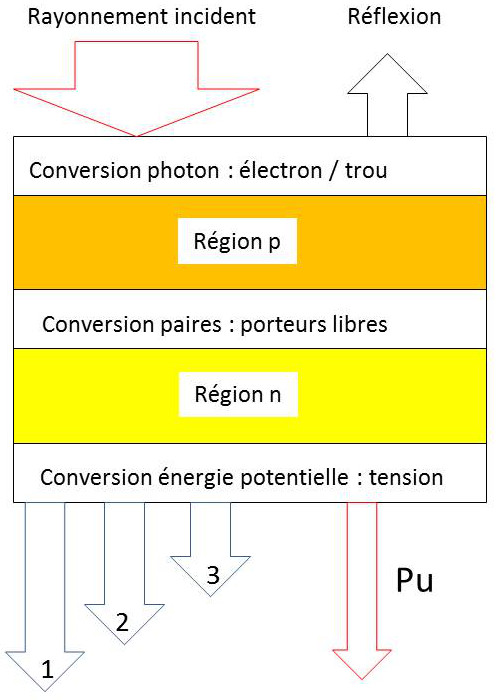Une cellule photovoltaïque comporte une jonction entre deux zones d’un même matériau (homo-jonctions p-n, dopées différemment) ou bien entre deux matériaux (hétéro-structures). La moins épaisse, ou celle de largeur de bande interdite la plus grande, est soumise au flux lumineux. Chacune des régions est reliée à une électrode métallique au moyen d’un contact ohmique de faible résistance.

Le principe de fonctionnement peut être décomposé en deux parties : l’absorption des photons et la collecte des porteurs de charge créés. Considérons une cellule illuminée par un flux de photons d’intensité $J(h\nu)$.

Selon leur énergie, les photons sont réfléchis (coefficient $R$), absorbés (coefficient $a$) ou transmis. Les photons absorbés, seuls utiles à la génération de l’effet voltaïque, sont ceux dont l’énergie $h\nu$ est supérieure ou égale à la largeur de bande interdite du matériau ($Eg\approx~1,1~eV$ dans le silicium). Le rendement d’absorption s’écrit : $$\eta_a=\frac{E_g\int_{E_g}^\infty (1-R)~e^{-aD}~J(h\nu)~d(h\nu)}{\int_{E_0}^\infty h\nu~J(h\nu)~d(h\nu)}$$

$D$ est l’épaisseur de la cellule.

Dans le cas du silicium, ce rendement est de l’ordre de 40 %.

L’énergie des photons absorbés sert partiellement à briser une liaison de valence qui crée de ce fait une paire électron - trou susceptible de se mouvoir. L’énergie excédentaire est rapidement cédée au réseau cristallin sous forme de chaleur (phonons).

Les paires ainsi crées – principalement au voisinage de la surface éclairée – vont diffuser vers la face arrière sous l’action d’une force qui est liée à leur gradient de concentration (effet Dember). Un grand nombre d’entre elles se recombinent en chemin, suivant un phénomène inverse de celui de l’absorption, et sont perdues pour le processus de conversion.

Les paires qui atteignent la zone de charge d’espace sont alors séparées : le champ électrique de la jonction accélère les électrons vers la région $n$ et les trous vers la région $p$. L’accumulation de ces charges dans des régions où elles sont minoritaires donne naissance à une différence de potentiel aux bornes de la cellule en circuit ouvert ($V_{oc}$).

Si les bornes sont fermées sur une résistance d’utilisation $R_c$, un courant $I_c$ s’établira dans le circuit ainsi constitué. Le courant maximal $I_{sc}$ est obtenu quand on court-circuite les bornes de la cellule ($R_c~=~0$). La cellule se comporte donc comme un générateur de puissance électrique. Le courant maximal étant proportionnel au nombre de paires électrons - trous collectées, on définit un rendement de collecte en formant le rapport entre le courant maximal et le courant $I_{\lambda}$, équivalent au flux total des photons incidents : $$\eta_c=\frac{I_{sc}}{I_{\lambda}}$$

Pour le silicium, ce rendement est de l’ordre de 53 % :

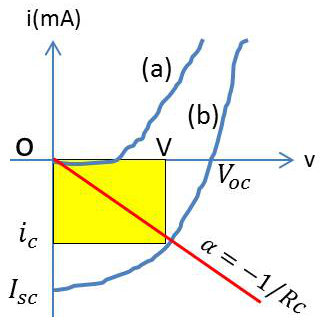La puissance fournie au circuit extérieur par la cellule éclairée dépend de la valeur de la résistance de charge $R_c$ ; cette puissance est maximale quand, sur le schéma ci-joint, la surface colorée de la courbe $I=f(V)$ est maximale, soit $V_m~I_m$. La courbe (a) montre le fonctionnement de la cellule dans l’obscurité, la courbe (b) sous éclairement.

Introduisons ce que l’on appelle le facteur de courbe : $$f_c=\frac{V_m~I_m}{V_{oc}}$$

Cette quantité $f_c<1$, généralement de l’ordre de 0,85, est importante pour l’efficacité de conversion, le rendement de la photopile étant défini comme le rapport : $$\eta=\frac{V_m~I_m}{\text{Énergie totale incidente}}=\eta_a~\eta_c~f_c$$

Pour une énergie totale incidente de 1 kW/m² (en condition AM1, c’est-à-dire pour un rayonnement traversant 1 fois l’épaisseur de la couche atmosphérique), le rendement d’une photopile silicium de structure simple (à jonction p-n comme celle décrite ci-dessus) aura un rendement de l’ordre des 20 %.

Remarque

Les spécialistes du photovoltaïque utilisent comme unité de référence la puissance crête (maximale) débitée par une photopile à 25 °C sous une puissance lumineuse incidente fixée pour les tests d’évaluation à 1 kW/m². La distribution spectrale du rayonnement solaire dépend de l’épaisseur de l’atmosphère à traverser, certaines normes (AMx ou air-masse) doivent être respectées.

Pour les applications terrestres, la photopile est placée au niveau de la mer dans des conditions d’éclairement qui correspondent à un ciel parfaitement clair et dégagé, sous un soleil de midi au zénith (90°) pour AM 1 ou d’inclinaison (42°) pour AM 1.5. Plus le nombre d’unités de masse sera élevé, plus le spectre solaire se décalera vers le proche infrarouge.