1. Théorèmes fondamentaux
1.1. Enoncé
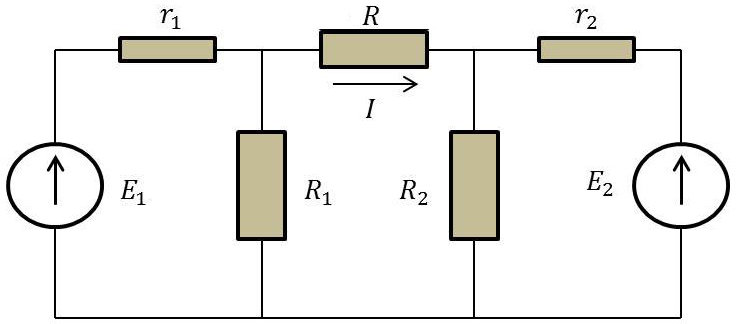On considère le réseau ci-contre en régime permanent. Déterminer l’expression littérale du courant \(I\) circulant dans la résistance \(R\) en appliquant les six méthodes d’analyse possibles :
-
méthode de Kirchoff,
-
méthode des courants de maille,
-
méthode des tensions de noeuds ;
-
théorème de superposition,
-
théorème de Thévenin,
-
théorème de Norton.
1.2. Solution
Nous donnons à priori l’expression de la formule recherchée : \[I=\frac{E_1~R_1~(r_2+R_2)-E_2~R_2~(r_1+R_1)}{r_1~R_1~(r_2+R_2)+r_2~R_2~(r_1+R_1)+R~(r_1+R_1)~(r_2+R_2))}\]
et établirons les formules de base pour chacune des six méthodes applicables.
1.2.1. Méthode de Kirchoff
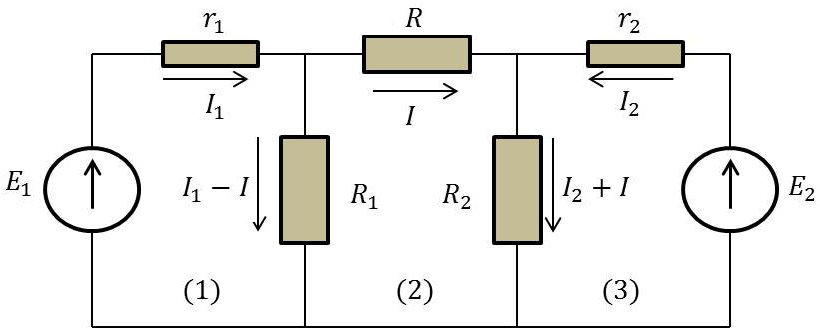En suivant la loi des intensités, on peut écrire pour chacune des trois mailles : \[\left\{ \begin{aligned} E_1&=r_1~I_1+R_1~(I_1-I)\\ 0&=R~I+R_2~(I_2+I)-R_1~(I_1-I)\\ E_2&=r_2~I_2+R_2~(I_2+I) \end{aligned} \right.\]
La résolution de ce système linéaire en (\(I_1,~I_2,~I\)) conduit à l’expression recherchée.
1.2.2. Méthode des courants de maille
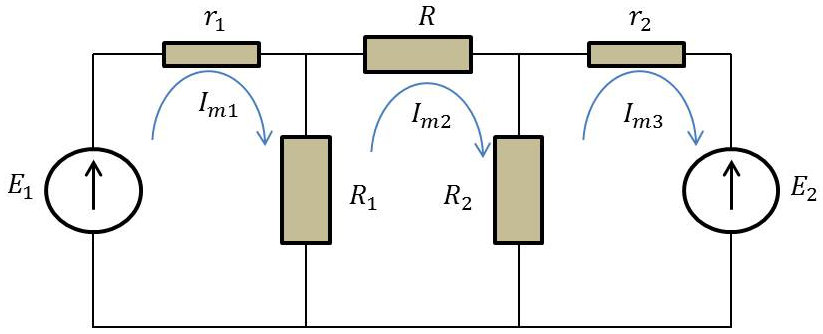On considère le réseau constitué de trois mailles indépendantes parcourues par les courants fictifs respectifs \(I_{mi}\) et circulant dans un sens choisi, à priori le même sens pour faciliter l’établissement des relations.
Le courant fictif \(I_{m2}\) est en fait confondu avec le courant réel I à déterminer.
La méthode de calcul est identique à celle de la méthode de Kirchoff : \[\left\{ \begin{aligned} E_1&=r_1~I_{m1}+R_1~(I_{m1}-I_{m2})\\ 0&=R_1~(I_{m2}-I_{m1})+R~I_{m2}+R_2~(I_{m3}-I_{m2})\\ E_2&=r_2~I_{m3}+R_2~(I_{m3}-I_{m2}) \end{aligned} \right.\]
1.2.3. Méthode de tension des nœuds
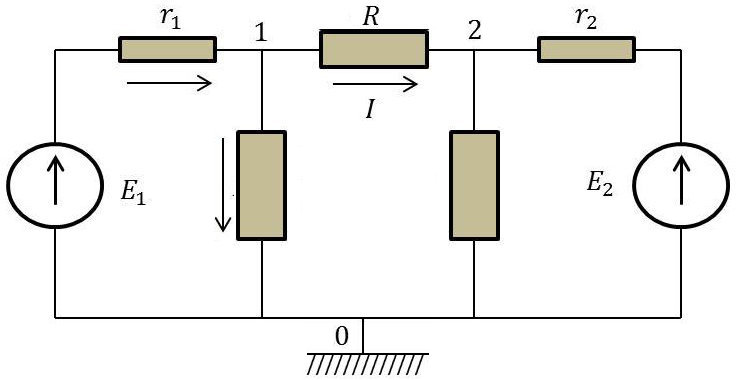On transforme les deux générateurs de tension en générateurs de courant équivalents.
On écrit les deux relations aux nœuds (1) et (2) qui conduiront aux tensions \(V_1,~V_2\) en ces points :
\[\begin{aligned} \text{Nœud (1) :}\qquad \frac{E_1-V_1}{r_1}=\frac{V_1}{R_1}+\frac{V_1-V_2}{R}\\ \text{Nœud (2) :}\qquad \frac{E_2-V_2}{r_2}=\frac{V_2}{R_2}+\frac{V_2-V_1}{R}\end{aligned}\]
On écrit ensuite que : \[I=\frac{V_1-V_2}{R}\]
et on retrouve la formule annoncée.
1.2.4. Théorème de superposition
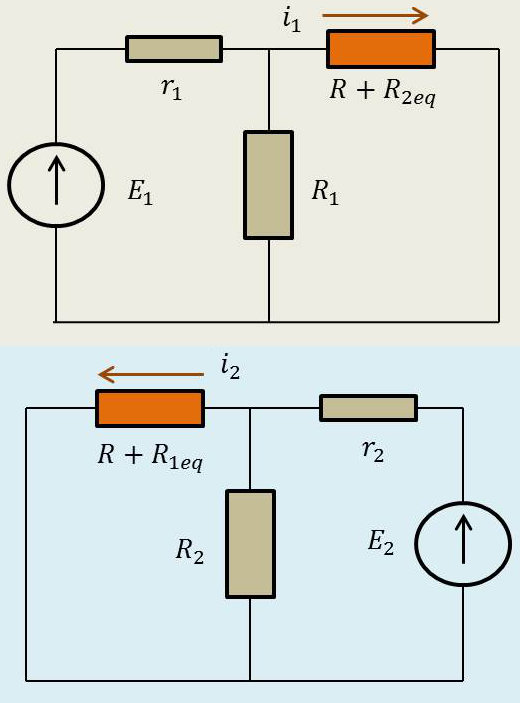On considère l’état (\(E_1,~E_2\)) comme la superposition des états (\(E_1,~0\)) et (\(0,~E_2\)).
Traitons le cas de l’état 1 (\(E_1,~0\)).
Expression de la résistance équivalente (\(R_2~//~r_2\)) : \[R_{2eq}=\frac{r_2~R_2}{r_2+R_2}\]
Deuxième résistance équivalente (\(R_1~//~R+R_{2eq}\)) : \[R'_{2eq}=\frac{R_1~R_{2eq}}{R_1+R_{2eq}}\]
On est ramené au circuit simple du générateur en série avec les résistances \(r_1\) et \(R'_{2eq}\)) ; il suffit d’appliquer la loi d’ohm. Tous calculs faits : \[i_1=E_1~\frac{r_1~(r_2+R_2)}{r_1~\{(R_1+R)(r_2+R)+r_2~R_2\}+R_1\{R(r_2+R_2)+r_2~R_2\}}\]
Même résultat pour \(i_2\) de l’état (\(0,~E_2\)) en effectuant les échanges d’indices \(1\leftrightarrow 2\).
On écrit ensuite (superposition) que : \[I=i_1+i_2\]
1.2.5. Théorème de Thévenin
Rappel du théorème
Tout réseau dipolaire de bornes A et B est équivalent à un générateur de tension et une résistance en série avec ce générateur.
Circuit ouvert (\(I=0\)), sa fém est \(E_{equ}=V_A-V_B\).
Sources éteintes (annulation des fém du réseau), sa résistance interne \(R_{equ}\) est celle de l’ensemble des résistances dispersées entre A et B.
Application
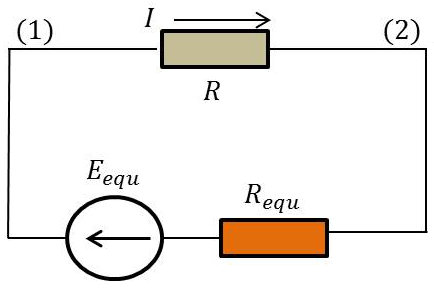Résistances des parties respectivement gauche \(r_1//R_1\) et droite \(r_2//R_2\) : \[R_{1equ}=\frac{r_1R_1}{r_1+R_1}\quad;\quad R_{2equ}=\frac{r_2R_2}{r_2+R_2}\]
Fém équivalente : \[E_{equ}=(V_1-V_2)_{I=0}=(V_1-V_0)_{I=0}+(V_0-V_2)_{I=0}\]
Remarquant les deux montages en potentiomètre pour \(V_1-V_0\) et \(V_0-V_2\) : \[E_{equ}=E_1~\frac{R_1}{r_1+R_1}-E_2~\frac{R_2}{r_2+R_2}\]
Résistance interne (entre 1 et 2), sources éteintes : \[R_{equ}=\frac{r_1~R_1}{r_1+R_1}+\frac{r_2~R_2}{r_2+R_2}\]
D’où le courant I circulant dans la résistance R : \[I=\frac{E_{equ}}{R_{equ}+R}\]
et on retrouve la formule attendue.
1.2.6. Théorème de Norton
Rappel du théorème
Tout réseau dipolaire de bornes A et B est équivalent à un générateur de courant et une résistance en parallèle avec ce générateur.
En court-circuit (\(V_A-V_B=0\)), il existe un courant \(I_0\) électromoteur (ou cém).
Sources éteintes, la conductance interne de \(R_{equ}\) est : \(G_{equ}=\cfrac{1}{R_{equ}}=\cfrac{1}{R_{AB}} \)
Application
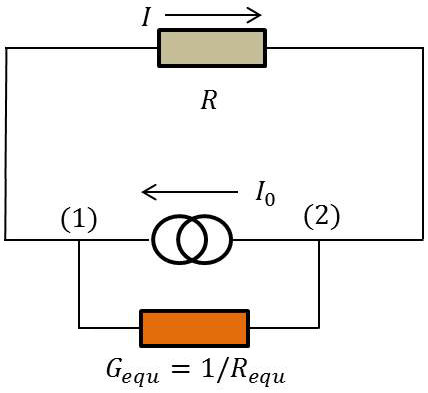Le générateur de courant équivalent au réseau entre (1) et (2) est caractérisé par :
– sa conductance \(G_{equ}=\cfrac{1}{R_{equ}}\), sachant que la résistance équivalente \(R_{equ}\) est celle calculée pour le générateur de Thévenin (paragraphe précédent).
– son courant caractéristique \(I_0\) (courant électromoteur) obtenu en mettant les bornes (1) et (2) en court-circuit (\(R=0\)) : \[I_0=I_{}cc=\frac{E_1~R_1~(r_2+R_2)-E_2~R_2~(r_1+R_1)}{r_1~R_1~(r_2+R_2)+r_2~R_2~(r_1+R_1)}\]
On écrit ensuite que : \[I=I_0+G_{equ}(V_2-V_1)=I_0-G_{equ}~R~I\]
C’est-à-dire : \[I=I_0~\frac{1}{1+\cfrac{R}{R_{equ}}}\]
et partant de là, le calcul conduit au résultat connu.
