1. Aspect descriptif

1.1. Représentations, diagrammes

• Représentation en bâtons.

• Représentation en histogramme (forme en escalier) par valeurs correspondant à un ensemble d’intervalles.

• Polygone des effectifs : ligne brisée obtenue en joignant les points situés aux centres de ces intervalles.

1.2. Série statistique

Si les éléments d’un même ensemble présentent tous un caractère commun dont on peut apprécier l’importance et si l’on repère celle-ci pour chaque élément de l’ensemble, cet ensemble des couples élément – caractère constitue une série statistique.

La représentation classique est celle du tableau.

On utilise aussi la représentation dite polygone des effectifs cumulés. Le graphe correspondant est en fait celui d’une fonction de répartition.

Dans l’exemple ci-dessous : \[\begin{bmatrix} 0&2&4&6&8&\cdots \\ 0&2&8&16&22&\cdots \end{bmatrix}\]

On aura : \(F(n<8)~=~0~+~2~+~8~+~16~=~26\)

2. Caractéristiques

Une série statistique est caractérisée par deux paramètres : position et dispersion.

2.1. Caractéristiques de position

2.1.1. Mode

On appelle mode la position en valeur la plus fréquente. S’il y a deux modes, le plus important sera le mode absolu et l’autre le mode relatif.

2.1.2. Médiane

La moitié au plus de l’effectif a un caractère de valeur [\(V<a\)].

La moitié au plus de ce même effectif a un caractère de valeur [\(V>a\)].

Noter que ce point correspond au point à mi-hauteur de la courbe des effectifs cumulés.

2.1.3. Quartile

Répartition par quarts. \(Q_1\) : quartile inférieur ; \(Q_3\) : quartile supérieur à la médiane.

La courbe des effectifs peut être mise à profit comme pour la médiane.

2.1.4. Moyenne

Moyenne arithmétique : \[\overline{X}~=~\dfrac{\sum_in_i~x_i}{n}~=~\sum k_i~x_i\qquad\text{avec :}\quad k_i=\frac{n_i}{n}\]

Moyenne géométrique : \[n~\log G~=~\sum k_i~\log x_i\]

Moyenne harmonique : \[\frac{1}{H}~=~\sum\frac{n_i}{n}~\frac{1}{x_i}~=~\sum\frac{k_i}{x_i}\]

2.2. Caractéristiques de dispersion

2.2.1. Intervalle inter-quartiles

Intervalle \(\Delta Q = Q_3-Q_1\).

2.2.2. Écart moyen

Défini par rapport à la moyenne \(m\) ou la médiane \(a\) : \[\begin{aligned} E_m~&=~\frac{\sum_i n_i~|x_i-m|}{n}~=~\sum_i\cup_i~|x_i-m|\\ E_a~&=~\frac{\sum_i n_i~|x_i-a|}{n}~=~\sum_i\cup_i~|x_i-a|\end{aligned}\]

2.2.3. Fluctuation ou variance

\[\sigma^2~=~\frac{\sum_i n_i~(x_i-m)^2}{n}\]

2.2.4. Coefficient de corrélation

\[r~=~\frac{\sum(x_i-\overline{x})~\sum(y_i-\overline{y})}{\sqrt{\sum(x_i-\overline{x})^2~\sum(y_i-\overline{y})^2}}\] \[\begin{aligned} &r~=~\pm 1 && \text{linéarité} \\ &r = 0 && \text{caractères indépendants} \\ 0<~&r<1 && \text{corrélation positive}\\ -1<~&r<0 && \text{corrélation négative}\end{aligned}\]

3. Problèmes d’ajustements

La méthode de lissage des points expérimentaux porte le nom de méthode des moindres carrés.

On dispose d’un certain nombre de points de mesure \((x_i,~y_i)\). On cherche alors une relation de la forme :  \(y~=~\phi(a_1,~a_2,~\cdots,~x)\).

Il s’agit de rendre minimale la forme : \[\sum_{i=1}^n \{(y_i-\phi(x_i)\}^2\]

D’où une suite de relations (avec a, b, etc.) : \[\begin{aligned} &\sum_{i=1}^n\{y_i-\phi(x_i~;~a,~b,~\cdots)\}~\frac{\partial\phi}{\partial a}~=~0\\ &\left.\frac{\partial\phi}{\partial a}\right|_i~=~\phi'_a (x_i~;~a,~b\cdots )\end{aligned}\]

3.1. Droite de régression

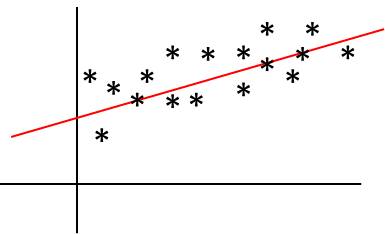
Le cas typique est celui de la droite : \[y~=~\phi(x~;~a~,~b) \qquad y~=~ax~+~b\]

D’où l’ensemble des dérivées : \[\frac{\partial y}{\partial a}=x_i \qquad;\qquad \frac{\partial y}{\partial b}=1\]

D’où le système linéaire en a et b à résoudre : \[\begin{aligned} \sum_{i=1}^n \{y_i-(a~x_i+b)~x_i\}~=~0 \quad &\Rightarrow \quad \left(\sum x_i^2\right)~a~+~\left(\sum x_i\right)~b~=~ \sum x_i~y_i \\ \sum_{i=1}^n \{y_i-(a~x_i+b) \}~=~0 \quad &\Rightarrow \quad \left(\sum x_i\right)a~+~n~b~=~0\end{aligned}\]

On peut également écrire directement : \[y-m_y~=~\frac{\sigma_{xy}}{\sigma^2}~(x-m_x)\]

3.2. Approximation parabolique

On a cette fois les relations : \[\begin{aligned} y&=a~x^2+b~x+c \\ \frac{\partial y}{\partial a}&=x^2 \quad ; \quad \frac{\partial y}{\partial b}=x \quad ; \quad \frac{\partial y}{\partial c}=1 \end{aligned}\]

D’où le système à résoudre : \[\begin{aligned} \left(\sum x_i^2\right)~a~+~\left(\sum x_i\right)~b~+~n~c~&=~\sum y_i\\ \left(\sum x_i^3\right)~a~+~\left(\sum x_i^2\right)~b~+~\left(\sum x_i\right)~c~&=~\sum x_i~y_i \\ \left(\sum x_i^4\right)~a~+~\left(\sum x_i^3\right)~b~+~\left(\sum x_i^2\right)~c~&=~\sum x_i^2~y_i\end{aligned}\]

4. Aspects interprétatifs

Quelle est la validité de choix d’une probabilité dans la description de l’ensemble de valeurs ?

4.1. Règle du maximum de vraisemblance

On part de l’expression de la probabilité en fonction de la densité de probabilité \(f(x~;~a_1,~a_2,~\cdots)\) : \[P=\sum_i~f(x~;~a_1,~a_2,~\cdots) \quad;\quad P=\int f(x~;~a_1,~a_2,~\cdots)~dx\]

Suivant la forme de l’expression, on fera : \[\frac{\partial P}{\partial a_i}=0\quad\forall~i~\qquad ; \qquad \frac{\partial ~(\ln P)}{\partial a_i}=0\quad\forall~i\]

Pour mémoire, dans le cas de la loi de Poisson : \[f(x~;~a)~=~\frac{a^x}{x!}~e^{-a} \qquad \Rightarrow \qquad a~=~\frac{\sum x_i}{n}\]

4.2. Test du Khi²

Le test du \(\chi^2\) permet d’évaluer le choix d’une loi de probabilité : \[\chi^2~=~\sum_{j=1}^r \frac{(k_j-n~p_j^2)}{n~p_j}\]

• \(n\) : nombre d’expériences

• \(r<n\) : nombre de valeurs distinctes

• \(k_j\) : fréquences respectives d’apparition des valeurs

• \(p_j\) : probabilité à priori des \(x_i\)