1. Ensembles et sous-ensembles
1.1. Ensemble
Un ensemble \(E\) est une collection finie ou infinie d’objets qui sont appelés éléments de l’ensemble \(E\).
1.2. Sous-ensemble
Certains éléments de \(E\) ont des propriétés communes. Ils forment alors un sous-ensemble \(A\), appelé encore partie de \(E\).
Exemple
-
\(E\) : ensemble des entiers positifs
-
\(A\) : ensemble des entiers pairs
\[A\subset E\qquad\text{(A inclus dans E)}\]
Le reste (\(E~\text{sans}~A\)) est appelé complémentaire de \(A\) dans \(E\). Il es noté \(C_A\).
Dans l’exemple précédent, \(C_A\) est l’ensemble des entiers impairs.
2. Inclusion, union, intersection de parties
2.1. Inclusion
Soient \(X\) et \(Y\) deux parties de \(E\) et \(x\) un élément de \(E\), ce qui se note : \(x\in E\)
Si \(x\in X\) et si \(\forall x\in X\), on a : \(x\in Y\), alors \(X\) est inclus dans \(Y\), ce qui se note : \(X\subset Y\)
Remarques
\[\left\{ \begin{aligned} &X\subset Y\\ &Y\subset Z \end{aligned} \right. \quad\Rightarrow\quad X\subset Z\]
\[\left\{ \begin{aligned} &X\subset Y\\ &Y\subset X \end{aligned} \quad\Rightarrow\quad X=Y \right.\]
2.2. Union
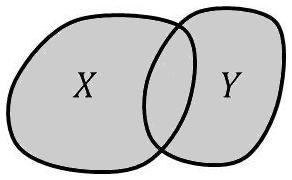On considère deux parties de \(E\) : \(X\subset E\) et \(Y\subset E\).
On appelle union, notée \(X\cup Y\), l’ensemble des points appartenant soit à la partie \(X\), soit à l’autre partie \(Y\) : \[x\in X\quad\text{ou}\quad x\in Y\]
Il s’agit donc de l’ensemble des points situés à l’intérieur des deux surfaces.
2.3. Intersection
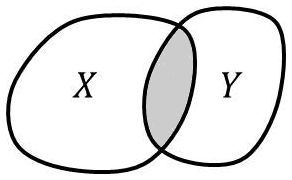L’intersection des ensembles \(X\) et \(Y\), notée \(X\cap Y\), est l’ensemble des éléments appartenant à la fois à \(X\) et à \(Y\) : \[x\in X\quad\text{et}\quad x\in Y\]
Si les parties \(X\) et \(Y\) n’ont pas d’éléments commun, on dit qu’elles sont disjointes. On écrit alors : \[X\cap Y=\oslash\qquad\text{(ensemble vide)}\]
3. Applications d’un ensemble dans un autre
3.1. Définition
Soient \(E\) et \(F\) deux ensembles distincts ou non.
Soit \(f\) une loi de composition qui à \(x\in E\) fait correspondre un unique \(y\in F\).
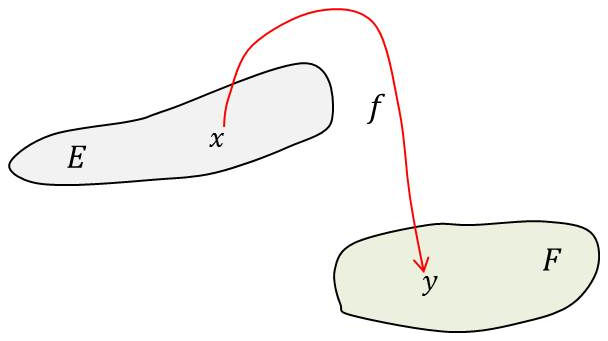\(f\) est une application de \(E\) dans \(F\), ou encore :
-
\(f\) est définie sur \(E\), à valeurs dans \(F\) ;
-
\(y\) est l’image de \(x\) par l’application \(f\).
On écrit :
\[\begin{aligned} f~:\quad E\quad&\rightarrow\quad F \\ x\quad&\rightarrow\quad y=f(x)\end{aligned}\]
On appelle image réciproque de \(y\) l’ensemble des \(x\) tels que \(y=f(x)\). Chacun de ces \(y\) est appelé antécédent de \(x\).
3.2. Application injective
Soit \(f\) une application de \(E\) sur \(F\).
\(f\) est dite injective (ou injection) quand tout élément de \(F\) a au plus un antécédent dans \(E\) : \[\forall x,~x'\in E\quad f(x)=f(x')\quad\Rightarrow\quad x=x'\]
3.3. Application surjective
Soit \(f\) une application de \(E\) sur \(F\).
\(f\) est dite surjective (ou surjection) quand tout élément de \(F\) a au moins un antécédent dans \(E\) : \[\forall y \in F\quad\exists x \in E\quad\text{tel que :}\quad y=f(x)\]
3.4. Application bijective ou biunivoque
Une application est dite bijective ou biunivoque (bijection) quand elle est à la fois injective et surjective. Ce qui revient à dire :
-
à tout élément de \(E\) correspond un unique élément de \(F\)
-
et à tout élément de \(F\) correspond un unique élément de \(E\).
Exemple
Soit \(\mathbb{R}\) l’ensemble des réels (positifs, négatifs et nul) et \(\mathbb{R}^+\) l’ensemble des réels (positifs ou nul). Considérons l’application \(f\) définie par : \[y=f(x)=x^2\]
\(f\) une application de \(\mathbb{R}\) dans \(\mathbb{R}\) et de \(\mathbb{R}\) sur \(\mathbb{R}^+\), non univoque : \[\textit{à}~~y\in\mathbb{R}^+\quad\rightarrow\quad\text{2 éléments}~\pm x\in\mathbb{R}\]
Par contre, si on prend \(y=x^2\) avec \(x\geq 0\), il y a application de \(\mathbb{R}^+\) sur \(\mathbb{R}^+\). L’application est cette fois biunivoque.
3.5. Application réciproque
Quand une application \(f\) de \(E\) sur \(F\) est bijective, on peut alors définir une application de \(F\) sur \(E\), appelée application réciproque et notée \(f^{-1}\), telle que : \[\forall y \in F,~\quad\forall y \in F~:\qquad y=f(x)\quad\Leftrightarrow\quad x=f^{-1}(y)\]
