1. Définitions

Soit l’espace euclidien à n dimensions \(\mathbb{R}_n\). Rapportons à cet espace une base \(\overrightarrow{x}_i\). Un point M est repéré par ses coordonnées \((x^1,~x^2,~\dots,~x^n)\).

On appelle distance de deux points \(x\) et \(y\) la quantité : \[||x-y||=\sqrt{(x^1-y^1)^2+(x^2-y^2)^2+\dots+(x^n-y^n)^2}\]

Un point \(x\in\mathbb{R}_n\) tend vers un point \(a\in\mathbb{R}_n\) quand :\( ||x-a||\rightarrow 0 \)

Si \(E\) est un sous-ensemble de \(\mathbb{R}_n\) (région), un point \(a\) sera adhérent à \(E\) s’il existe des points de \(E\) aussi proches que l’on veut du point \(a\), autrement dit : \[\forall~\varepsilon > 0~,\quad\exists~~x\in E\quad\text{tel que}\quad ||x-a||<\varepsilon\]

L’ensemble des points adhérents à \(E\) est appelé adhérence de \(E\) ou encore fermeture de \(E\).

Conséquences :

• \(E\) est contenu dans sa fermeture.

• Tous les points de \(E\) sont adhérents à eux-mêmes.

• Lorsque l’ensemble \(E\) s’identifie à sa fermeture, il est dit fermé.

1.1. Ensemble borné

Un ensemble borné n’a pas de points à l’infini. Un ensemble \(E\) est borné si la distance de tous ses points au point origine est bornée : \[\sqrt{x_1^2+x_2^2+\dots+x_n^2}~\leq~M\]

Quand l’ensemble est fermé et borné, il est dit compact.

Un ouvert de l’espace \(\mathbb{R}_n\) est le complémentaire d’un espace fermé

1.2. Connexité dans \(\mathbb{R}_3\)

Soit \(\mathcal R\) une région de cet espace \(\mathbb{R}_n\). On dit qu’elle est connexe si, quelque soit le couple \((a,~b)\) de points de \(\mathcal{R}\), on peut trouver un arc de courbe rectifiable, d’origine \(a\) et d’extrémité \(b\) contenue entièrement dans \(\mathcal{R}\).

\(\mathcal{R}\) étant une région connexe, elle sera dite simplement connexe si, quelque soit la courbe \((C)\) (close) contenue dans \(\mathcal{R}\), il existe une surface compacte \((S)\) ayant pour bord \((C)\) et toute entière contenue dans \(\mathcal{R}\).

Exemples

• Prenons dans \(\mathbb{R}_3\) la surface de la sphère. Elle est connexe : en prenant deux points, on aura toujours un arc rectifiable de l’un à l’autre. Elle est de plus simplement connexe.

• Soit le point \(O\in \mathbb{R}_3\). Le complémentaire de \(O\) est connexe et simplement connexe. En effet, sur une courbe quelconque \((C)\) ne passant pas par \(O\), on peut appliquer une surface compacte.

• Soit une droite \((D)\) de l’espace et son complémentaire. Celui-ci est connexe mais non simplement connexe, car une surface donnée peut être traversée par cette droite.

• Considérons à présent un tore. Il s’agit d’un domaine connexe mais non simplement connexe. En effet, sur une courbe \((C)\) faisant le tour du tore on ne peut appuyer de surface entièrement contenue dans le tore.

• Prenons le plan qui est un sous-espace de \(\mathbb{R}_3\). Il est connexe mais non simplement connexe.

2. Intégrale de courbe

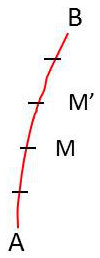Soit un arc de courbe rectifiable \(AB\) de longueur \(l\) et \(M\) un point courant de cette courbe : \[s=\stackrel{\frown}{AM}\qquad~0\leq s\leq l\]

On peut décomposer cet arc en segments infiniment petits et on suppose qu’à tout point \(M\) on peut associer une fonction scalaire notée \(f(M)\) réelle ou complexe.

On considère alors la somme : \[\sum_{p=1}^n f(M_{\xi})~\overline{M_{p-1}M_p}\qquad~p-1\leq\xi\leq p\]

Nous admettrons que, si cette courbe est rectifiable, cette somme tend vers une limite : \[\int_C f(M)~ds\qquad\text{notée encore :}\quad\int_C~f(s)~ds\]

D’un point de vue physique, si \(f(M\)) est la densité massique de la courbe, cette intégrale représentera la masse de la courbe. On dira que l’on a pris pour mesure la densité massique.

3. Élément différentiel de surface

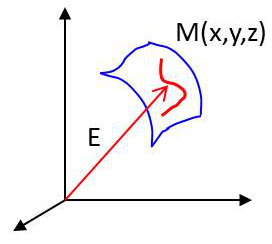Considérons une portion de surface compacte et \(M\) un point de cette surface.

L’équation paramétrique de la surface est donnée par : \[\big\{~x(u,v)~~;~~y(u,v)~~;~~z(u,v)~\big\}\]

On pourra ainsi poser : \[\overrightarrow{MO}=\overrightarrow{E(u,v)}\]

On appelle courbes coordonnées sur cette surface les courbes d’équations : \[\big\{~u=cte~~;~~v=cte~\big\}\]

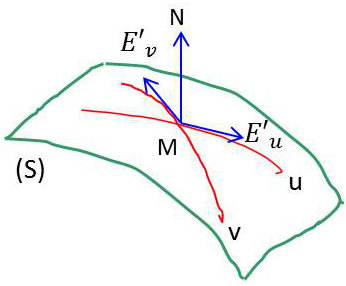Leur intersection est le point \(M\).

Considérons un point \(M + dM\) voisin de \(M\). Nous poserons : \[\overrightarrow{dM}=\overrightarrow{E'_u}~du+\overrightarrow{E'_v}~dv\]

On a respectivement sur chaque courbe :

\[\begin{aligned} \big\{~u=cte \quad;\quad \overrightarrow{MM'}=\overrightarrow{E'_v}~dv~\big\}\\ \big\{~v=cte \quad;\quad \overrightarrow{MM'}=\overrightarrow{E'_u}~du~\big\}\end{aligned}\]

La normale en \(M\) à la surface est perpendiculaire au plan tangent, donc à \(\overrightarrow{E'_u}\) et \(\overrightarrow{E'_v}\).

On a donc : \[\overrightarrow{N}~//~\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}\quad\qquad\overrightarrow{E'_u}(x'_u,~y'_u,~z'_u)~~;~~\overrightarrow{E'_v}(x'_v,~y'_v,~z'_v)\]

3.1. Équation du plan tangent au point M

En désignant les coordonnées courantes par \([X,Y,Z]\), on exprime l’orthogonalité de la normale et du plan tangent par : \[(X-x)~|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|_x+(Y-y)~|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|_y+(Z-z)~|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|_z\]

3.2. Équation de la normale au point M

On exprime la colinéarité avec le vecteur « normale » \[\frac{(X-x)}{|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|_x}=\frac{(Y-y)}{|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|_y}=\frac{(Z-z)}{|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|_z}\]

3.3. Calcul de la distance entre deux points

Reprenons la relation \[\overrightarrow{dM}=\overrightarrow{E'_u}~du~+~\overrightarrow{E'_v}~dv\]

On écrit que : \[(ds)^2=(\overrightarrow{E'_u})^2~(du)^2~+~(\overrightarrow{E'_v})^2~(dv)^2~+~ 2~\overrightarrow{E'_u}\cdot\overrightarrow{E'_v}~du~dv\]

Avec :

\[\begin{aligned} (\overrightarrow{E'_u})^2&={x'_u}^2+{y'_u}^2+{z'_u}^2\\ (\overrightarrow{E'_v})^2&={x'_v}^2+{y'_v}^2+{z'_v}^2\\ \overrightarrow{E'_u}\cdot\overrightarrow{E'_v}&=x'_ux'_v+y'_uy'_v+z'_uz'_v\end{aligned}\]

[1] L’équation d’une surface s’exprime souvent sous la forme explicite \(z=f(x,y)\).

En introduisant les courbes coordonnées \(u=cte\) et \(v=cte\)

et les coefficients directeurs : \[p=\frac{\partial z}{\partial u}=\frac{\partial z}{\partial x}\quad;\quad~q=\frac{\partial z}{\partial v}=\frac{\partial z}{\partial y}\]

sur les courbes coordonnées : \[\overrightarrow{E'_u}(1,0,p)\quad;\quad\overrightarrow{E'_v}(0,1,q)\]

on obtient : \[(ds)^2=(1+p)^2~(dx)^2+2~p~q~dx~dy+(1+q)^2~(dy)^2\]

[2] En coordonnées sphériques :

\[\begin{aligned} &x=R~\sin(\theta)~\cos(\varphi)\\ &y=R~\sin(\theta)~\sin(\varphi)\\ &z=R~\cos(\theta) \end{aligned} \qquad u=\theta \qquad v=\varphi\]

On a alors : \[\overrightarrow{E'_{\theta}}= \left\{ \begin{aligned} R~&\cos(\theta)~\cos(\varphi)~d\theta\\ R~&\cos(\theta)~\sin(\varphi)~d\theta\\ -R~&\sin(\theta)~d\theta \end{aligned} \right. \qquad \overrightarrow{E'_{\varphi}}= \left\{ \begin{aligned} -R~&\sin(\theta)~\sin(\varphi)~d\varphi\\ R~&\sin(\theta)~\cos(\varphi)~d\varphi\\ &0 \end{aligned} \right.\]

Et pour l’élément de surface : \[(ds)^2=(\overrightarrow{E'_{\theta}})^2+2~\overrightarrow{E'_{\theta}}~\overrightarrow{E'_{\varphi}}+(\overrightarrow{E'_{\varphi}})^2\]

4. Aire de surface

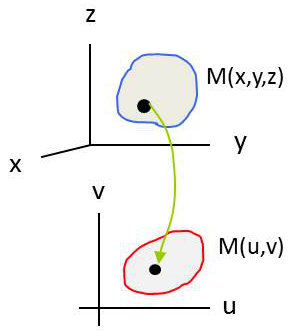Soit une surface compacte (fermée et bornée).

À un point \(M\in [O,x,y,z]\), on fait correspondre \(M\in [u,v]\).

Par quadrillage du deuxième domaine (courbes \(u=cte~;~v=cte\)), on peut connaître l’aire de la surface dans ce domaine.

Élément d’aire, un parallélogramme curviligne élémentaire : \[dA=|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|~du~dv\]

D’où l’aire totale : \[A=\iint\limits_{plan~(u,v)}|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|~du~dv\]

Cas particulier : \(z=f(x,y)\)

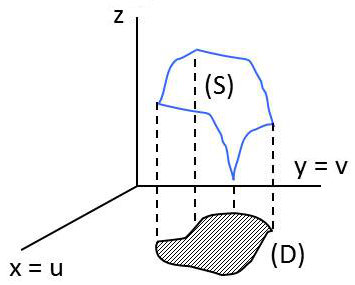On prend \((x=u~;~y=v)\). Le plan des \([u, v]\) est alors celui des \([x, y]\).

\(D\) est la projection de la surface \(S\) sur le plan \(xOy\) :

\[\begin{aligned} &\overrightarrow{E'_u}=(1,~0,~p)~~;~~\overrightarrow{E'_v}=(0,~1,~q)\\ &\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}=(-p,~-q,~1)\end{aligned}\]

Par suite : \[A=\iint\limits_D\sqrt{1+p^2+q^2}~dx~dy\]

Intégrale de surface

Soit une fonction \(f(M)\) définie et continue en chaque point.

Alors : \[I=\iint\limits_S f(M)~ds\] est une intégrale de surface : \[A=\iint\limits_D |\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|~du~dv\]

5. Circulation de vecteur sur un arc de courbe rectifiable

Soit \(M\) un point courant de l’arc rectifiable \(AB\) de longueur \(l\). \(M'\) est un point voisin de \(M\).

On peut écrire : \[\overrightarrow{MM'}=\overrightarrow{dM}=\overrightarrow{T}~ds\qquad s=\stackrel{\frown}{AM}\qquad~0\leq s\leq l\]

Supposons qu’en tout point \(M\) soit défini un champ vectoriel dont les composantes sont des fonctions continues : \[\sum_i\overrightarrow{V}(M_{\xi})\cdot\overrightarrow{M_iM_{i-1}}\qquad i-1<\xi<i\]

Si la courbe est rectifiable, la limite est : \[I=\int_C \overrightarrow{V}\cdot\overrightarrow{dM}=\int_C \overrightarrow{V}(M)\cdot\overrightarrow{T}~ds\]

Cette intégrale représentant physiquement un travail.

Expression analytique

Si l’on a :

\[\begin{aligned} &\overrightarrow{V_M}=\{P(x,y,z),~Q(x,y,z),~R(x,y,z)\}\\ \text{et}\\ &\overrightarrow{dM}=\{dx,~dy,~dz\}\end{aligned}\]

Il vient: \[I=\int_C P~dx+Q~dy+R~dz\]

Si, par ailleurs, les coordonnées sont fonction d’un autre paramètre (le temps par exemple) : \[x(t),~y(t),~z(t)\quad\Rightarrow\quad dx=x'_t~dt\quad\text{etc.}\]

On peut alors mettre l’expression sous la forme : \[I=\int_{t1}^{t2}\varphi(t)~dt\]