Sommaire

1. Répartition des masses
1.1. Centres et moments d’inertie
1.2. Tenseur d’inertie
1.3. Axes principaux d’inertie
1.4. Exemples types
2. Grandeurs associées aux vitesses
2.1. Résultante et moments cinétiques
2.2. Énergie cinétique
2.3. Composition de mouvements
3. Grandeurs associées aux accélérations
3.1. Forces d’inertie
3.2. Composition des mouvements

Le moment d’inertie $I$ du système par rapport à une droite $\Delta$ est égal au moment d’inertie $J$ par rapport à la droite parallèle à $\Delta$ issue du centre d’inertie $G$, augmentée du moment d’inertie par rapport à $\Delta$ de la masse totale $M$ supposée concentrée en $G$. \[I~=~J+M~d^2\]

On obtiendra d’ailleurs un résultat analogue avec les produits d’inertie.

On choisira à cet effet des axes issus du centre d’inertie, dans lesquels la droite $\Delta$ aura pour équations simples $[x = a,~y = b]$.

Les intégrales du type $\iiint x~dm$ et $\iiint y~dm$ sont nulles puisque le centre d’inertie coïncide avec l’origine des coordonnées.

Il reste donc les relations suivantes :

\[\begin{aligned} \iiint\{{(x-a)}^2+{(y-b)}^2\}~dm&=\iiint(x^2+y^2)~dm+M~(a^2+b^2)\\ \iiint(x-a)(y-b)~dm&=\iiint xy~dm +M~ab\end{aligned}\]

1.2. Tenseur d’inertie

En un point donné, à partir des moments et produits d’inertie relatifs à un système d’axes, on peut construire le tableau suivant : \[\begin{bmatrix} A&-F&-E\\ -F&B&-D\\ -E&-D&C \end{bmatrix}\]

Les éléments de ce tableau dépendent des axes choisis. Nous désignons par $T_{ij}$ l’élément qui appartient à la ligne de rang i et à la colonne de rang j.

Lorsqu’on effectue une rotation des axes, les nouvelles coordonnées $(x'_1,x'_2,x'_3)$ s’expriment en fonction des anciennes coordonnées $(x_1,x_2,x_3)$ par les relations : \[\begin{pmatrix} x'_1\\ x'_2\\ x'_3\\ \end{pmatrix} = \begin{pmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{pmatrix} \times \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}\]

Les éléments de cette matrice répondent aux conditions suivantes : \[\left\{ \begin{aligned} \sum_ia_{ij}.a_{ik}&=0\qquad j\neq k\\ \sum_i a_{ij}^2&=1 \end{aligned} \right.\]

Une notation plus conforme au calcul tensoriel consiste à exprimer les éléments de cette matrice sous la forme $a_i^j$.

La relation matricielle précédente deviendra alors : \[T_{ij}=a_i^l.a_j^m.T_{lm}\qquad\text{avec sous-entendu }\sum_{l,m}\]

L’ensemble ordonné des neuf nombres précédents constitue un tenseur de rang deux. C’est le tenseur d’inertie au point considéré. Il est symétrique et généralement désigné par le symbole $\Theta$.

On peut associer une transformation linéaire dont les coefficients sont les composantes de ce tenseur. À tout vecteur $\overrightarrow{u}$ de composantes $(\alpha,\beta,\gamma)$, cette transformation fait correspondre le vecteur $\overrightarrow{v}$ de composantes $y=\Theta.u$.

On pourra vérifier que : \[v~=~\iiint OP\wedge(u\wedge OP)~dm\]

Ce qui prouve que la correspondance entre les vecteurs est indépendante des axes.

Le moment d’inertie par rapport à une droite $\Delta$ passant par un point $O$ s’exprime à l’aide des composantes du tenseur d’inertie au point $O$.

$\overrightarrow{u}$ désignant un vecteur unitaire de $\Delta$, la distance d’un point M à la droite $\Delta$ est égale au module de $u\wedge OP$.

Remarquons que l’on peut écrire : \[r^2=(u\wedge OP)\cdot(u\wedge OP)=u\cdot\{OP\wedge(u\wedge OP)\}\]

On a alors : \[\iiint r^2dm=u\cdot\iiint OP\wedge(u\wedge OP)~dm=u\cdot\Theta.u\]

C’est-à-dire : \[I~=~A\alpha^2+B\beta^2+C\gamma^2-2D\beta\gamma-2E\gamma\alpha-2F\alpha\beta\]

1.3. Axes principaux d’inertie

Le vecteur propre du tenseur est défini par la relation matricielle $\Theta u=\lambda u$. La valeur propre associée étant obtenue à partir du polynôme caractéristique $D(\lambda)=0$. Les valeurs propres sont toutes réelles.

À chaque valeur caractéristique correspond au moins un vecteur propre $u$.

Les supports des vecteurs propres sont appelés axes principaux d’inertie. Le moment d’inertie par rapport au support du vecteur propre $u$ a pour valeur : \[I=u\cdot\Theta u=u\cdot\lambda u=\lambda u^2=\lambda\]

Il en résulte que les valeurs caractéristiques du tenseur d’inertie sont égales aux moments d’inertie par rapport aux axes principaux. Ces moments d’inertie sont appelés moments principaux d’inertie.

Ainsi les valeurs caractéristiques sont positives ou nulles.

Lorsqu’on choisit l’axe $Oz$ comme support de l’un des vecteurs propres, le système d’équations de base comporte la solution $(\alpha=\beta=0~;~\gamma=1]$, si bien que l’on a : $D=E=0$.

Réciproquement, si les produits d’inertie $D$ et $E$ sont nuls, $Oz$ est axe principal d’inertie. La répartition des vecteurs propres dépend de l’ordre de multiplicité des valeurs caractéristiques.

1.4. Exemples types

Barre rectiligne homogène

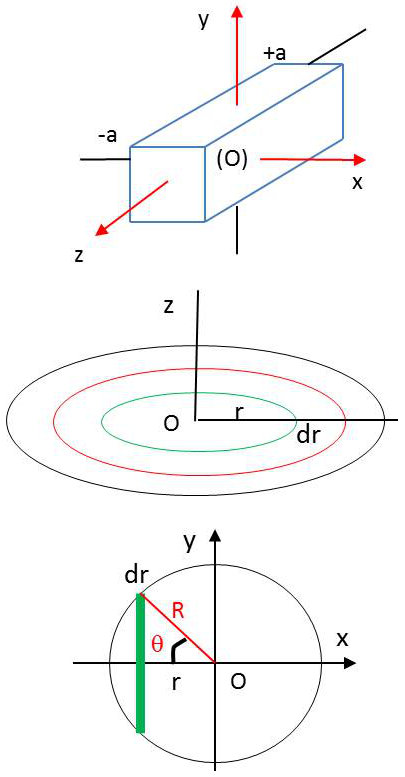Le centre d’inertie d’une barre rectiligne homogène est situé en son centre (centre de symétrie). On a :

\[\begin{aligned} &A=B=\int_{-a}^{+a}r^2(\mu~dr)=\frac{Ma^2}{3}\\ &C=0\end{aligned}\]

Disque homogène

Pour un disque homogène, par rapport à l’axe $Oz$ : \[C=\int_0^R r^2\mu~(2h~dr)=\frac{MR^2}{2}\]

Par rapport aux axes $Ox$ et $Oy$ (résultats identiques pour des raisons évidentes de symétrie) : \[I=\int_0^R r^2\mu~(2h~dr)\]

Effectuant le changement de variable :

\[\begin{aligned} &r=R\cos(\theta)\qquad\qquad \theta\in[0,\pi]\\ &dr=-r~\sin(\theta)~d\theta\end{aligned}\]

et sachant que :

\[\begin{aligned} 4\sin^2(\theta)~\cos^2(\theta)&=\sin^2(2\theta)\\ \sin^2(2\theta)&=\frac{1-\cos(4\theta)}{2}\end{aligned}\]

on obtient, tous calculs faits : \[A=B=\frac{MR^2}{4}\]

Sphère pleine homogène

Pour une sphère pleine homogène, par raison de symétrie, $A = B = C$.

Considérant comme élément de volume une couronne sphérique d’épaisseur $dr$ :

\[\begin{aligned} I&=\int_0^R r^2\mu~\Big(\frac{4}{3}~\pi r^2~dr\Big)\\ M&=\mu~\Big(\frac{4}{3}~\pi R^3\Big)\end{aligned}\]

On obtient ainsi : \[A=B=C=\frac{2}{5}~M~R^2\]

On retiendra le résultat suivant :

Le centre d’inertie d’un solide de révolution, homogène, d’axe $Oz$ est situé sur $Oz$. Les calculs de moments d’inertie principaux en un point de l’axe $Oz$ sont ramenés au calcul de deux intégrales simples :

\[\begin{aligned} &S=\iiint z^2~dm=\int \mu~z^2~\pi r^2~dz\\ &C=\iiint (x^2+y^2)~dm=\mu~(\frac{r^2}{2})~\pi r^2~dz\\ &A=B=S+\frac{C}{2}\end{aligned}\]

2. Grandeurs associées aux vitesses

2.1. Résultante et moments cinétiques

Soit un point $P$, de masse $m$ et de vitesse $V$ :

On appelle quantité de mouvement du point le vecteur $m~V$.

On appelle moment cinétique du point par rapport à $O$ le produit vectoriel $H=OA\wedge mV$ dont les composantes sont : \[\left\{ \begin{aligned} &H_x=m~(y\dot{z}-z\dot{y})\\ &H_y=m~(\dot{x}-x\dot{z})\\ &H_z=m~(x\dot{y}-y\dot{x}) \end{aligned} \right.\]

Le moment cinétique par rapport à une droite $\Delta$ de vecteur unitaire u et passant par $O$ a pour expression : \[(OP\wedge mV)\cdot u\]

Si l’on considère maintenant le solide comme un ensemble de points matériels, ce système sera caractérisé par les trois relations : \[\left\{ \begin{aligned} &\iiint OP~dm=M~OG\\ &\iiint V~dm=M~V_G\\ &H=\iiint OP\wedge(V~dm) \end{aligned} \right.\]

Dans le cas d’un solide animé d’un mouvement de translation, le torseur des quantités de mouvement est équivalent au torseur unique $M.V_G$, quantité de mouvement du centre d’inertie doué de la masse totale.

Dans le cas d’un solide animé d’un mouvement de rotation $\omega$ autour d’un point fixe $O$, le moment cinétique en $O$ est égal au produit du tenseur d’inertie en ce point par le vecteur rotation : \[H=\iiint OP\wedge(\omega\wedge OP)~dm=\mathcal{J}~\omega\]

L’expression analytique des composantes du moment cinétique sur des axes quelconques est donnée par : \[\left\{ \begin{aligned} &H_x=Ap-Fq-Er\\ &H_y=-Fp+Bq-Dr\\ &H_z=-Ep-Dq+Cr \end{aligned} \right.\]

Les composantes sur des axes principaux d’inertie du point $O$ sont données par : \[H_x=Ap\quad;\quad H_y=Bq\quad;\quad H_z=Cr\]

Le moment cinétique ainsi que le vecteur rotation sont colinéaires lorsque ce dernier est porté par le support d’un vecteur propre, c’est-à-dire lorsque le solide tourne autour d’un axe principal d’inertie.

2.2. Énergie cinétique

Soit un point $M$ de masse $m$, animé d’une vitesse $V$.

On appelle énergie cinétique du point le demi-produit de la masse par le carré de la vitesse. L’énergie cinétique T d’un système est la somme des énergies cinétiques de ses éléments : \[2~T=\iiint V^2~dm\]

Pour un solide en translation : \[2~T=\iiint V^2~dm=M~V^2\]

Pour un solide en rotation autour d’un point fixe $O$ :

\[\begin{aligned} &V^2=(\omega\wedge OP)\centerdot(\omega\wedge OP)=\omega\cdot\{OP\wedge(\omega\wedge OP)\}\\ &2~T=\omega\cdot\iiint OP\wedge(\omega\wedge OP~dm)\\ &2~T=\omega\cdot\mathcal{J}.d=\omega\cdot H\end{aligned}\]

L’énergie cinétique s’exprime en fonction des composantes du tenseur $\mathcal{J}$ et du vecteur $\omega$ :

\[\begin{aligned} &2~T=Ap^2+Bq^2+Cr^2-2Dqr-2Erp-2Fpq &&\text{axes quelconques}\\ &2~T=Ap^2+Bq^2+Cr^2 &&\text{axes principaux d'inertie}\end{aligned}\]

Le moment d’inertie par rapport à l’axe de rotation a pour valeur $I=u\cdot\mathcal{J}.u$, le vecteur $u$ étant unitaire sur cet axe.

On en déduit l’expression : \[2~T=I~\omega^2\]

2.3. Composition de mouvements

Si le mouvement d’un système résulte de deux autres mouvements, le torseur des quantités de mouvement est équivalent au torseur formé par les quantités de mouvement relatives et par les quantités de mouvement d’entrainement.

Si la position d’un système dépend de plusieurs paramètres, le torseur des quantités de mouvement est équivalent au torseur formé par les quantités de mouvement qu’aurait le système si chaque paramètre variait séparément.

On peut interpréter le mouvement d’un système $S$ par rapport à des axes fixes $O_1x_1y_1z_1$ en menant par le centre d’inertie $G$ des axes $Gxyz$ parallèles aux axes fixes.

Le mouvement résulte d’une translation de vitesse $V_G$ et d’une rotation autour du point $G$.

Dans la translation, la résultante cinétique est nulle puisque le point $G$ est fixe, tandis que le moment cinétique en $G$ est un certain vecteur $H_G$.

Théorème

Le moment cinétique $OH$ d’un système matériel par rapport à un point $O$ est la somme du moment cinétique qu’aurait le système si toute la masse était concentrée au centre d’inertie $G$ et du vecteur $H_G$, moment cinétique du système par rapport au point $G$ dans son mouvement autour de $G$, rapporté au trièdre $Gxyz$.

La loi de composition des vitesses ($V=V_r+V_e$) permet d’écrire la loi de composition des énergies cinétiques sous la forme suivante : \[\iiint V^2~dm=\iiint V_r^2~dm+\iiint V_e^2.dm+2\iiint V_rV_e~dm\]

En règle générale, l’énergie cinétique n’est pas égale à la somme de l’énergie cinétique relative et de l’énergie cinétique d’entrainement, sauf cas particulier (orthogonalité des deux vitesses). C’est le cas par exemple lorsque le mouvement relatif est celui d’une figure plane dans son plan, tandis que le mouvement d’entrainement est une rotation autour d’un axe situé dans le plan.

3. Grandeurs associées aux accélérations

3.1. Forces d’inertie

Soit un point $P$ de masse $m$, de vitesse $V$, d’accélération $\gamma$. On appelle respectivement quantité d’accélération de ce point le vecteur $m\Gamma$, et force d’inertie du point le vecteur $-m\Gamma$.

La force d’inertie d’un point matériel admet une composante tangentielle $-m~dV/dt$ et une composante normale $mV^2/R$. La composante normale est dirigée dans la direction opposée à la direction du centre de courbure : c’est force d’inertie centrifuge.

Dans un système matériel, les forces d’inertie $-\Gamma~dm$ de ses éléments forment un torseur qui admet pour résultante générale $-m\Gamma_G$, force d’inertie qu’aurait le centre d’inertie si toute la masse y était concentrée.

Le moment résultant $OK$ des forces d’inertie par rapport à un point $O$ est égal, au signe près, à la vitesse du moment cinétique $OH$ :

\[\begin{aligned} &\iiint OP~dm=M~OG\\ &\iiint -\Gamma~dm=-M~\Gamma_G\\ &OK=\iiint OP\wedge(-\Gamma~dm)=-\frac{d}{dt} \iiint OP\wedge V~dm\end{aligned}\]

Dans le cas d’un solide en translation, le torseur des forces d’inertie est équivalent au vecteur unique $-M~\Gamma_G$, force d’inertie du centre d’inertie, doté de la masse totale.

Calcul de composantes

Considérons à présent un solide $S$ animé d’une rotation autour du point $O$ par rapport à des axes $Ox_1y_1z_1$. La résultante générale des forces d’inertie est égale à $-M~\Gamma_G$. Le moment résultant $OK$ des forces d’inertie par rapport au point $O$ est égal à la vitesse changée de signe du moment cinétique $OH=\mathcal{J}.\omega$.

Dans le trièdre $Oxyz$ animé d’une rotation $\Omega$ par rapport au trièdre $Ox_1y_1z_1$, nous désignerons par :

\[\begin{aligned} &A,B,C,D,E,F &&\text{les composantes du tenseur d’inertie au point O}\\ &p,q,r &&\text{les composantes de la rotation $\omega$}\\ &P,Q,R &&\text{les composantes de la rotation $\Omega$}\end{aligned}\]

On a les relations suivantes : \[\left\{ \begin{aligned} H_x&=Ap-Fq+Er\\ H_y&=-Fp+Bq-Dr\\ H_z&=-Ep-Dq+Cr \end{aligned} \right. \qquad \left\{ \begin{aligned} K_x&=-\{\dot{H}_x+Q.H_z-R.H_y\}\\ K_y&=-\{\dot{H}_y+R.H_x-P.H_z\}\\ K_z&=-\{\dot{H}_x+P.H_y-Q.H_x\} \end{aligned} \right.\]

Dans le cas particulier où le trièdre intermédiaire $Oxyz$ est lié au solide $S$, la rotation $\Omega$ se confond avec la rotation $\omega$ du solide $S$.

Si en outre, on choisit pour axes $Oxyz$ des axes principaux d’inertie, les équations précédentes s’écrivent sous une forme simplifiée : \[\left\{ \begin{aligned} K_x&=-\{A\dot{p}+(C-B)~q~r\}\\ K_y&=-\{B\dot{q}+(A-C)~r~p\}\\ K_z&=-\{C\dot{r}+(B-A)~p~q\} \end{aligned} \right.\]

Dans le cas d’un solide de révolution autour d’un axe $Oz$, il est commode d’adopter comme trièdre intermédiaire le trièdre $Ouvz$ qui a permis de caractériser les angles d’Euler. On obtient : \[\left\{ \begin{aligned} H_u&=A\dot{\theta}\\ H_v&=A\dot{\psi}\sin(\theta)\\ H_z&=C(\dot{\psi}\cos[\theta)+\dot{\varphi}] \end{aligned} \right. \qquad \left\{ \begin{aligned} P&=\dot{\theta}\\ Q&=\dot{\psi}\sin(\theta)\\ R&=\dot{\psi}\cos(\theta) \end{aligned} \right. \qquad \left\{ \begin{aligned} p&=\dot{\theta}\\ q&=\dot{\psi}\sin(\theta)\\ r&=\dot{\psi}\cos(\theta)+\dot{\varphi} \end{aligned} \right.\]

3.2. Composition des mouvements

Si le mouvement d’un système matériel résulte de deux mouvements, un mouvement relatif et un mouvement d’entrainement de rotation $\Omega$, le torseur de ses forces d’inertie équivaut au torseur formé par les vecteurs suivants :

\[\begin{aligned} &-\Gamma_r~dm &&\text{forces d’inertie relatives}\\ &-\Gamma_e~dm &&\text{forces d’inertie d'entrainement}\\ &-2~\Omega\wedge(V_r~dm) &&\text{forces d’inertie complémentaires}\end{aligned}\]

On peut interpréter le mouvement du système $S$ par rapport à des axes fixes $O_1x_1y_1z_1$ en menant par le centre d’inertie $G$ des axes $Oxyz$ parallèles aux axes fixes.

Le mouvement résulte d’une translation et d’une rotation autour du point $G$. Dans la translation, le torseur des forces d’inertie est équivalent au vecteur unique $-M~\Gamma_G$ issu du point G. Dans le mouvement de $S$ par rapport aux axes $O_1x_1y_1z_1$, la résultante générale des forces d’inertie est nulle puisque le point G est fixe, tandis que le mouvement résultant en $G$ des forces d’inertie est un certain vecteur $K_G$.

Théorème

Le torseur des forces d’inertie d’un système est équivalent au torseur formé par le vecteur $(-M~\Gamma_G)$ , force d’inertie qu’aurait la masse totale si elle était concentrée au centre d’inertie, et par le couple d’axe $K_G$, constitué par les forces d’inertie du système dans son mouvement autour du centre d’inertie.

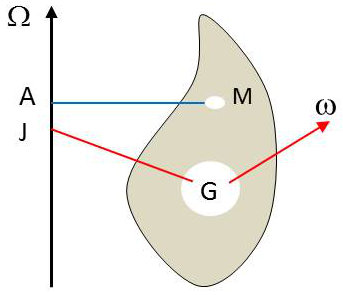À titre d’exemple, nous allons calculer les forces d’inertie et les forces d’entrainement complémentaires dans le cas d’un solide animé d’un mouvement relatif arbitraire, le mouvement d’entrainement étant une rotation uniforme $\Omega$ autour d’un axe fixe $O_1z_1$.

Nous désignons par $G$ le centre d’inertie du solide et par $J$ la projection orthogonale du point $G$ sur l’axe $O_1z_1$. Un point arbitraire $M$ du solide se projette en orthogonalement en $A$ sur $O_1z_1$.

La masse totale du solide est désignée par $M$, sa rotation relative par $\omega$ et la vitesse relative du centre d’inertie par $V_G$.

Forces d’inertie d’entrainement

La résultante générale $R$ et le moment résultant $K$ au point $G$ des forces d’inertie d’entrainement s’expriment par :

\[\begin{aligned} &R=\iiint AP~\Omega^2~dm=M~JG~\Omega^2\\ &K=\iiint GP\wedge(AP~\Omega^2)~.dm\end{aligned}\]

Forces d’inertie complémentaires

La résultante générale $R$ et le moment résultant $K$ au point $G$ des forces d’inertie complémentaires s’expriment par :

\[\begin{aligned} &R=\iiint -2~\Omega\wedge(V_G+\omega~GP)~dm=-2~M~\Omega\wedge V_G\\ &K=\iiint GP\wedge\{-2~\Omega\wedge(V_G+\omega\wedge GP)\}~dm\end{aligned}\]

Certaines astuces de calcul vectoriel permettent de simplifier les écritures avant de passer à l’intégration proprement dite.

Actualisé le 2014-03-27

↑ Haut

II. Cinétique

Plan du site

1. Répartition des masses

1.1. Centres et moments d’inertie