Sommaire

1. Définition de la vitesse
2. Vitesse des points d’un solide
2.1. Introduction des angles d’Euler
3. Composition des vitesses
4. Mouvements à surfaces de contact
5. Mouvements plans
6. Étude des accélérations
6.1. Définition de l’accélération
6.2. Composition des accélérations

Étant donné un torseur $[T]$ dont les éléments de réduction en un point fixe $O$ dépendent du temps, les vecteurs d’origine $O$ et équipollents aux vitesses de ces éléments de réduction constituent eux-mêmes les éléments de réduction d’un nouveau torseur noté $[\dot{T}]$ indépendant du point $O$ et appelé torseur dérivé du torseur :

\[\begin{aligned} &AB &&\text{Composantes} &&X,~Y,~Z\\ &\Big\{\frac{d(AB)}{dt}\Big\}_S &&\text{Composantes} &&\dot{X},~\dot{Y},~\dot{Z}\\ &[T] &&\text{Éléments de réduction} &&OR,~OG\\ &[\dot{T}] &&\text{Éléments de réduction} &&\frac{d}{dt}OR,~\frac{d}{dt}OG\end{aligned}\]

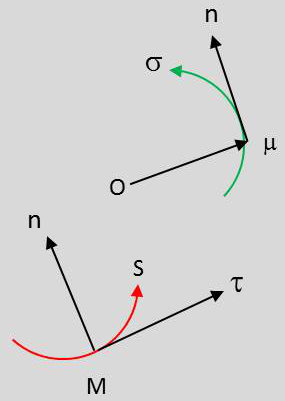$La courbe $(\sigma)$ est l’indicatrice des tangentes à $(S)$$ La vitesse d’un point $M$ en mouvement par rapport à un trièdre $Oxyz$ est la dérivée du vecteur $OM$.

Le lieu $(C)$ du point $M$ est la trajectoire.

L’abscisse curviligne est désignée par $s$.

Le vecteur unitaire de la tangente orientée dans le sens des $s$ croissants est donné par : \[\tau=\frac{dM}{ds}\]

Le lieu de l’extrémité du vecteur $O\mu$ équipollent à $\tau$ s’appelle l’indicatrice des tangentes.

On peut toujours supposer que l’abscisse curviligne $\sigma$ du point $\mu$ varie dans le même sens que $s$.

Le vecteur unitaire de la tangente à l’indicatrice orientée dans le sens des $\sigma$ croissants est équipollent au vecteur unitaire de la normale principale à la courbe $(C)$.

En résumé, on a donc :

\[\begin{aligned} V&=\frac{dM}{dt}\qquad\qquad\qquad\text{Composantes}\qquad \dot{x}=\frac{dx}{dt},~~\dot{y}=\frac{dy}{dt},~~\dot{z}=\frac{dz}{dt}\\ V&=\frac{dM}{ds}~\frac{ds}{dt}=\tau~\frac{ds}{dt}\\ n&=\frac{d\tau}{d\sigma}~~;~~R=\frac{ds}{d\sigma}~~;~~\frac{d\tau}{dt}=n~\frac{V}{R}\end{aligned}\]

La règle de dérivation des fonctions composées permet d’énoncer :

Lorsque la position d’un point $M$ dépend de plusieurs paramètres, sa vitesse est la somme des vitesses qu’il aurait si chaque paramètre variait isolément.

Si la position du point $M$ dépend de trois paramètres $q_1,~q_2,~q_3$, on a :

\[\begin{aligned} &V=\frac{dM}{dt}=\frac{\partial M}{\partial q_1}~\dot{q}_1+\frac{\partial M}{\partial q_2}~\dot{q}_2+\frac{\partial M}{\partial q_3}~\dot{q}_3\\ &V=V_1+V_2+V_3\end{aligned}\]

$Composantes du vecteur vitesse [$V_r,V_{\theta},V_{\psi}$] en coordonnées polaires [r,\theta,\varphi]$ En coordonnées polaires ($r,~\theta$), les composantes de la vitesse sont $\dot{r}$ sur le rayon vecteur et sur l’axe directement perpendiculaire, de vecteur unitaires respectifs ($\vec{i},~\vec{j}$).

La vitesse a pour expression : \[V=\dot{r}~i+(r\dot{\theta})~j\]

En coordonnées sphériques ($r,~\theta,~\psi$) :

\[\begin{aligned} &x=r~\sin(\theta)~\cos(\varphi) &&V_r=\dot{r}\\ &y=r~\sin(\theta)~\sin(\varphi) &&V_{\theta}=r~\dot{\theta}\\ &z=r~\cos(\theta) &&V_{\psi}=r~\sin(\theta)~\dot{\psi}\end{aligned}\]

2. Vitesse des points d’un solide

Généralement, l’espace fixe est rapporté au trièdre $Ox_1y_1z_1$ et l’espace mobile au trièdre $Oxyz$.

Dans un mouvement de translation, tous les vecteurs liés au solide demeurent équipollents à eux-mêmes, donc tous les points du solide ont des vitesses équipollentes, ce qui est trivial, le solide étant supposé indéformable.

La rotation d’un solide autour d’un axe provient du fait qu’une droite liée au solide demeure fixe, l’axe de coordonnée $Oz_1$, du trièdre de référence $Ox_1y_1z_1$, par exemple.

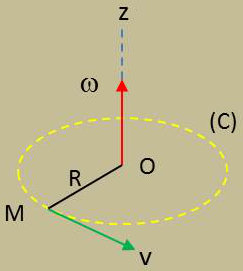On désigne par $V$ le vecteur vitesse (tangent à la trajectoire), $\omega $ le vecteur rotation (de module $\dot{\alpha}=ds/dt$, $R$ le module de $OM$ et $\dot{\alpha}$ celui de $\omega$ : \[V=\frac{ds}{dt}=\frac{R.d\alpha}{dt}=R~\dot{\alpha}\]

$OM$ et $\omega$ sont orthogonaux, on peut donc poser a priori : \[V=\omega\wedge OM\]

Dans un mouvement de rotation autour d’un point fixe, la position d’un solide mobile dépend de trois paramètres.

2.1. Introduction des angles d’Euler

Il est souvent commode d’adopter comme paramètres les trois angles d’Euler ($\psi,\theta,\varphi$) qui caractérisent la position du trièdre $Oxyz$ par rapport au trièdre $Ox_1y_1z_1$ de l’espace fixe.

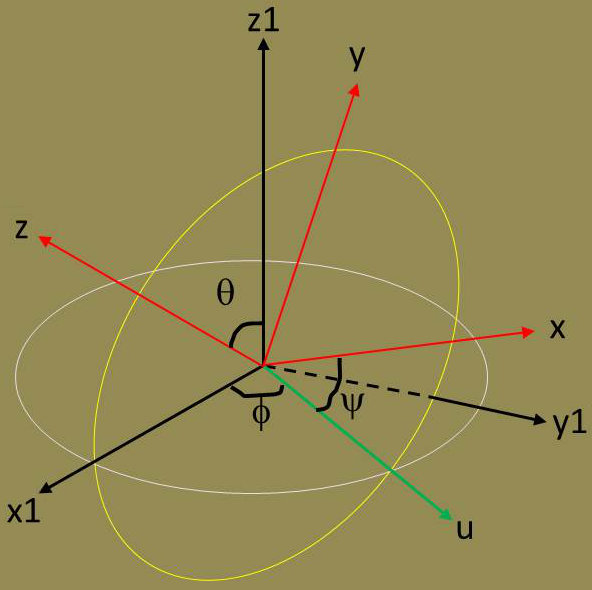$Repère avec les angles d’Euler : rotation propre $\varphi$, précession $\psi$ et nutation $\theta$$ Le plan mobile [$Ox,Oy$] et le plan fixe [$Ox_1,Oy_1$] se coupent suivant une droite $Ou$ appelée ligne nodale, perpendiculaire à la fois à $z_1$ et à $z$ et orientée arbitrairement.

Le plus souvent, le sens positif sera celui du produit vectoriel $Oz_1\wedge Oz$.

Les angles d’Euler sont définis comme suit :

Précession : $\psi=\widehat{x_1Ou} \quad \in[0,2\pi]$
sens positif de rotation autour de $Oz_1$
Nutation : $\theta=\widehat{z_1Oz} \quad \in[0,\pi]$
sens positif de rotation autour de $Ou$
Rotation propre : $\varphi=\widehat{uOx} \quad \in[0,2\pi]$
sens positif de rotation autour de $Oz$

Les composantes du vecteur vitesse angulaire $\Omega$ sur les axes mobiles $Oxyz$ peuvent être exprimés en fonction des angles d’Euler et de leurs dérivées $\dot{\psi},~\dot{\theta},~\dot{\varphi}$.

La rotation ($Oz_1,\psi$) fait passer des axes $Ox_1y_1z_1$ aux axes $Ouv_1z_1$.

Les coordonnées d’un même point dans les deux systèmes sont liées par la transformation linéaire dont la matrice est désignée par $D$ : \[\left\{ \begin{array}{r l} &u=x_1\cos(\psi)+y_1\sin(\psi)\\ &v1=-x_1\sin(\psi)+y_1\cos(\psi)\\ &z=z_1 \end{array} \right. \qquad D= \begin{pmatrix} \cos(\psi)&\sin(\psi)&0\\ -\sin(psi)&\cos(psi)&0\\ 0&0&1 \end{pmatrix}\]

La rotation ($Ou,\theta$) fait passer des axes $Ouv_1z_1$ aux axes $Ouvz$.

Les coordonnées d’un même point dans les deux systèmes sont liées par la transformation linéaire dont la matrice est désignée par $C$ : \[\left\{ \begin{array}{r l} &u=u\\ &v=v_1\cos(\theta)+z_1\sin(\theta)\\ &z=-v_1\sin(\theta)+z_1\cos(\theta) \end{array} \right. \qquad C= \begin{pmatrix} 1&0&0\\ 0&\cos(\theta)&\sin(\theta)\\ 0&-\sin(\theta)&\cos(\theta) \end{pmatrix}\]

La rotation ($Oz,\varphi$) fait passer des axes $Ouvz$ aux axes $Oxyz$.

Les coordonnées d’un même point dans les deux systèmes sont liées par la transformation linéaire dont la matrice est désignée par $B$ : \[\left\{ \begin{array}{r l} &x=u\cos(\varphi)+v\sin(\varphi)\\ &v=-u\sin(\varphi)+v\cos(\varphi)\\ &z=z \end{array} \right. \qquad B= \begin{pmatrix} \cos(\varphi)&\sin(\varphi)&0\\ -\sin(\varphi)&\cos(\varphi)&0\\ 0&0&1 \end{pmatrix}\]

Remarque

Désignons par $\omega_{z1},~\omega_u,~\omega_z$ les vecteurs portés par $Oz_1,~Ou,~Oz$ respectivement et ayant pour mesures $\dot{\psi},~\dot{\theta},~\dot{\varphi}$.

Décomposons le mouvement pour un point M :

$\psi$ varie seul : rotation / $Oz_1\quad~~$ vitesse de M : $V1=\omega_{z1}\wedge OM$
$\theta$ varie seul : rotation / $Ou\qquad$ vitesse de M : $V2=\omega_u\wedge OM$
$\varphi$ varie seul : rotation / $Oz\qquad$ vitesse de M : $V3=\omega_z\wedge OM$

Dans le cas général, la vitesse d’un point M est donnée par la formule :

\[\begin{aligned} &V=V_1+V_2+V_3=\omega\wedge OM\\ &\omega=\omega_{z1}+\omega_u+\omega_z\qquad\qquad\omega~:~\text{rotation instantanée}\end{aligned}\]

Les composantes du vecteur $\omega$ sur les axes $Ouvz$ sont données par les formules :

\[\begin{aligned} &\omega_u=\dot{\theta}\\ &\omega_v=\dot{\psi}\sin(\theta)\\ &\omega_z=\dot{\psi}\cos(\theta)+\dot{\varphi}\end{aligned}\]

Les composantes du vecteur $\omega$ suivant les systèmes d’axes mobile ou fixe sont donnés par : \[\begin{array}{r l} &\omega_x=\dot{\psi}\sin(\theta)\sin(\varphi)+\dot{\theta}\cos(\varphi)\\ &\omega_y=\dot{\psi}\sin(\theta)\cos(\varphi)-\dot{\theta}\sin(\varphi)\\ &\omega_z=\dot{\psi}\cos(\theta)+\dot{\varphi} \end{array} \qquad \begin{array}{r l} &\omega_1=\dot{\varphi}\sin(\theta)\sin(\varphi)+\dot{\theta}\cos(\psi)\\ &\omega_2=-\dot{\varphi}\sin(\theta)\cos(\psi)+\dot{\theta}\sin(\psi)\\ &\omega_3=\dot{\varphi}\cos(\theta)+\dot{\psi} \end{array}\]

3. Composition des vitesses

Trois solides $S_1,~S_2,~S_3$ sont en mouvement les uns par rapport aux autres.

On dit que le mouvement de $S_3$ par rapport à $S_1$ résulte du mouvement de $S_3$ par rapport à $S_2$ (mouvement relatif) et du mouvement de $S_2$ par rapport à $S_1$(mouvement d’entrainement).

Selon le théorème de composition des vitesses : \[V=V_r+V_e\]

$\qquad\qquad V_r$ vitesse relative ($M/S_2$, en supposant fixe $S_2/S_1$)

$\qquad\qquad V_e$ vitesse d’entrainement ($M$ fixe de $S_2$ et mobile /$S_1$)

Le mouvement le plus général d’un solide $S$ attaché à un système $Oxyz$ peut être interprété comme un mouvement de rotation du solide autour du point $O$ considéré comme fixe, suivi d’une translation de ce système d’axes par rapport à un système réellement fixe $O_1x_1y_1z_1$.

La vitesse $V$ est alors le moment résultant en $M$ du torseur qui, au point $O$ admet $\omega$ (vecteur rotation) pour résultante générale et $V_0$ pour moment résultant. On a donc : \[V=V_0+\omega\wedge OM \qquad \left\{ \begin{array}{r l} V_x=\dot{x}_0+qz-ry\\ V_y=\dot{y}_0+rx-pz\\ V_z=\dot{z}_0+py-qx \end{array} \right.\]

La vitesse par rapport au repère $S_1$ constitué par les axes $O_1x_1y_1z_1$ d’un vecteur lié au solide $S$ est donnée par : \[\frac{d(AB)}{dt}=V_B-V_A=\omega\wedge AB\]

La vitesse d’un vecteur non lié à $S$ est donnée par : \[\{\frac{d(AB)}{dt}\}_{S1}=\{\frac{d(AB)}{dt}\}_S+\omega\wedge AB\]

Le deuxième terme représente la vitesse d’entrainement. Lorsqu’on parle de la vitesse d’un vecteur, il est nécessaire de préciser le repère. Si le vecteur $\omega$ est fixe par rapport à $S_1$, il est fixe par rapport à $S$ et réciproquement.

La première formule peut être appliquée aux vecteurs unitaires $\vec{i},~\vec{j},~\vec{k}$ des axes liés à $S$. En désignant par$p,~q,~r$ les composantes sur ces axes de la rotation $\omega$, on obtient les formules :

\[\begin{aligned} &\frac{d\vec{i}}{dt}=r\vec{j}-q\vec{k}\\ &\frac{d\vec{j}}{dt}=p\vec{k}-r\vec{i}\\ &\frac{d\vec{k}}{dt}=q\vec{i}-p\vec{j}\end{aligned}\]

Lorsqu’on prend pour le solide $S$ le trièdre de Frenet d’une courbe gauche, les vecteurs $\vec{i},~\vec{j},~\vec{k}$ sont remplacés par les vecteurs unitaires $\vec{\tau},~\vec{n},~\vec{b}$ portés par la tangente, la normale principale et la binormale. D’après les formules établies au paragraphe 1, on a : $q=0~;~r=V/R$.

On pose $p=V/T$ et on donne à la grandeur $T$ ainsi définie le nom de rayon de torsion de la courbe. On obtient alors les formules :

\[\begin{aligned} \omega&=\frac{V}{T}~\tau+\frac{V}{R}.b\\ \frac{d\tau}{dt}&=V~\frac{n}{R}\\ \frac{dn}{dt}&=V~\Big\{\frac{b}{T}-\frac{\tau}{R}\Big\}\\ \frac{db}{dt}&=-V~\frac{n}{T}\end{aligned}\]

4. Mouvements à surfaces de contact

Un mouvement important que l’on rencontre en mécanique est celui d’une surface mobile constamment tangente à une surface fixe. Il est alors commode de considérer le trièdre géodésique d’une courbe tracée sur une surface pour son étude.

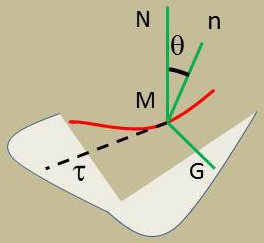On appelle géodésique d’une courbe $C$ tracée sur une surface $S$ le trièdre formé par le vecteur unitaire $\tau$ de la tangente à la courbe orientée dans le sens des abscisses curvilignes croissantes, le vecteur unitaire $G$ normal à la courbe, tangent à la surface et orienté arbitrairement, et le vecteur unitaire $N=\tau\wedge G$.

On désigne par $\theta$ l’angle $(n,N)$ mesuré avec le sens des rotations positives autour de $\tau$ :

\[\begin{aligned} n=N\cos(\theta)+G\sin(\theta)\\ b=N\sin(\theta)-G\cos(\theta)\end{aligned}\]

La rotation $\omega$ du trièdre géodésique est égale à la rotation du trièdre de Frenet augmentée de la rotation $\tau~\dot{\theta}$ du trièdre géodésique par rapport à ce trièdre.

En posant :

\[\begin{aligned} \frac{1}{R_N}&=\frac{\cos\theta}{R}\\ \frac{1}{R_G}&=-\frac{\sin\theta}{R}\\ \frac{d\tau}{dt}&=V~\Big\{\frac{N}{R_N}-\frac{G}{R_G}\Big\}\end{aligned}\]

on peut alors écrire :

\[\begin{aligned} &\omega=\frac{V}{T}~\tau+\frac{V}{R}~b+\frac{d\theta}{dt}~\tau\\ &\omega=\Big\{\frac{V}{T}+\frac{d\theta}{dt}\Big\}~\tau-\frac{V}{R_N}~G-\frac{V}{R_G}~N\end{aligned}\]

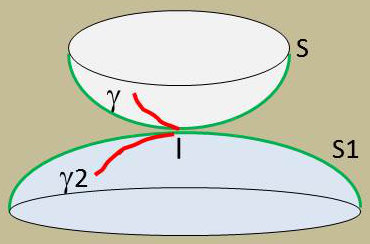Considérons maintenant un solide $S$ qui se déplace en restant constamment en contact avec un solide fixe $S_1$. À l’instant t, nous désignons par $I$ le point de contact, par $U$ la vitesse du point lié à $S$ et qui coïncide avec $I$, par $\omega$ la rotation de $S$ par rapport à $S_1$. Le cas où le point $S$ serait un point singulier pour la surface de l’un des solides est exclu.

Le point $I$ décrit sur $S$ une trajectoire $\gamma$ et sur $S_1$ une trajectoire $\gamma_1$.

La vitesse de $I$ par rapport à $S_1$ est la somme de sa vitesse par rapport à $S$ et de la vitesse d’entrainement $U$. Cette dernière se trouve donc dans le plan tangent commun.

On décompose le vecteur $\omega$ en un vecteur $\omega_T$ situé dans le plan tangent commun et un vecteur $\omega_N$ normal à ce plan.

Les vecteurs précédents sont désignés par :

$U$ : vitesse de glissement de $S$ sur $S_1$
$\omega_T$ : vitesse angulaire de roulement de $S$ sur $S_1$
$\omega_N$ : vitesse angulaire de pivotement de $S$ sur $S_1$

Lorsque $U=0$, on dit que les deux solides roulent sans glisser l’un sur l’autre. Les trajectoires $\gamma$ et $\gamma_1$ sont alors tangentes et décrites avec la même vitesse $V$. Dans ce cas, la rotation $\omega$ s’exprime en fonction des courbures géodésiques des trajectoires $\gamma$ et $\gamma_1$.

En particulier, le pivotement s’annule lorsque les trajectoires $\gamma$ et $\gamma_1$ et possèdent des courbures géodésiques égales :

\[\begin{aligned} \Big\{\frac{d\tau}{dt}\Big\}_{S1}&=\Big\{\frac{d\tau}{dt}\Big\}_{S}+\omega\wedge\tau\\ \omega_N&=V~\Big\{\frac{1}{R_G}-\frac{1}{R_{G1}}\Big\}\end{aligned}\]

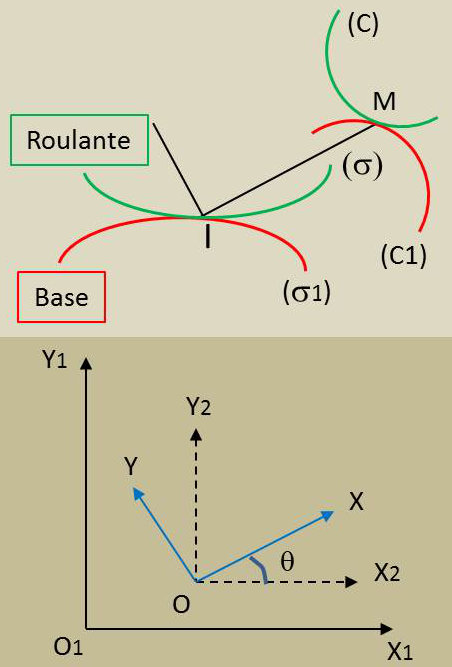
5. Mouvements plans

Un solide $S$ est animé d’un mouvement plan s’il existe un plan $P$ lié à $S$ qui glisse sur un plan fixe $P_1$. Le mouvement d’un plan mobile $Oxy$ sur un plan fixe $O_1x_1y_1$ peut être décomposé. Dans ce but, on introduit deux axes intermédiaires $Ox_2y_2$ parallèles aux axes fixes $O_1x_1y_1$.

On peut considérer que le mouvement est le résultat de deux mouvements:

une translation de vitesse $V_0$ ;
une rotation de vitesse angulaire $\omega$ autour d’un axe issu du point O et perpendiculaire au plan $Oxy$.

$Mouvement plan de roulement sans glissement ($\sigma$) appelée roulante sur ($\sigma_1$) appelée base$ La vitesse d’un point $M$ est le moment résultant en $M$ du torseur défini par sa résultante générale $\omega$ et son moment résultant en $O$, c’est-à-dire $V_0$.

Ces éléments étant perpendiculaires, le torseur est équivalent à un torseur unique équipollent à $\omega$ et passant par un point $I$ du plan : \[V_M=V_0+\omega\wedge OM=\omega\wedge IM\]

La distribution des vitesses est la même que si la plan tournait autour du point $I$ avec la vitesse angulaire $\omega$. Ce point $I$ est appelé centre instantané de rotation.

La vitesse angulaire s’obtient en dérivant par rapport au temps l’angle $\theta$ que fait une droite arbitraire $Ox$ du plan mobile avec une droite arbitraire $O_1x_1$ du plan fixe.

Les normales aux trajectoires des points liés au plan mobile passent par $I$.

Un point $M$ mobile par rapport au plan $Oxy$ décrit dans ce plan une trajectoire $C$ avec la vitesse $V$ et, dans le plan $O_1x_1y_1$ une trajectoire $C_1$ avec la vitesse : \[V=V_r+\omega\wedge IM\]

Les trajectoires $C$ et $C_1$ seront tangentes en $M$ si $IM$ est normal à $C$. Pour cela, il faut et il suffit que $M$ soit le pied d’une normale abaissée du point $I$ sur $C$. La vitesse de glissement de $C$ sur $C_1$ est égale au produit vectoriel $\omega\wedge IM$.

Le seul point du plan mobile qui ait une vitesse nulle par rapport au plan $O_1x_1y_1$ est celui qui se trouve en $I$.

Les trajectoires $\sigma_1$ et $\sigma_2$ du centre instantané de rotation $I$ dans les plans $Oxy$ et $O_1x_1y_1$ respectivement sont deux courbes décrites avec la même vitesse ; le glissement est nul.

$Détermination du centre instantané de rotation J, point où la normale MN à la courbe glissante C touche son enveloppe $\gamma$$ Tout mouvement plan peut être interprété comme le roulement sans glissement d’une courbe $\sigma$ appelée roulante sur une courbe $\sigma_1$ appelée base.

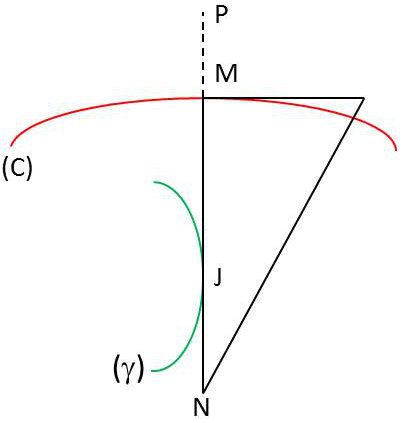
Prenons un exemple. Le plan lié à la tangente et à la normale en un point M d’une courbe $C$ glisse sur le plan de $C$. La normale $MN$ à $C$ touche son enveloppe $\gamma$ en un point $J$.

Dans le mouvement plan que l’on vient de définir, le centre instantané de rotation se trouve d’une part sur la normale en $M$ à $C$, d’autre part sur la normale commune à la droite $MN$ et à son enveloppe $\gamma$. Le centre de rotation instantanée est donc le point $J$.

On en déduit d’une part que la normale $MN$ roule sans glisser sur son enveloppe (cette enveloppe est appelée développée de $C$, d’autre part que tout point $P$ situé sur $MN$ à une distance fixe de $M$ décrit une courbe parallèle $C$.

6. Étude des accélérations

6.1. Définition de l’accélération

Le vecteur vitesse d’un point $M$ est une fonction du temps. Quand elle existe, la dérivée $\Gamma$ du vecteur vitesse $V$ du point $M$ est l’accélération du point $M$. Le lieu de l’extrémité d’un vecteur d’origine fixe et équipollent à $V$ s’appelle hodographe du mouvement du point $M$. La vitesse du point $\mu$ est égale à l’accélération $\Gamma$.

Les composantes de l’accélération sur les axes du trièdre de Frenet de la trajectoire s’obtiennent par dérivation de l’égalité $V=V\tau$.

L’accélération est contenue dans le plan osculateur (composantes tangentielle $\dot{V}$ et normale $V^2/R$) :

\[\begin{aligned} \Gamma&=\frac{dV}{dt}=\frac{d^2M}{dt^2}\qquad\qquad\text{composantes : }~ \ddot{x},\ddot{y},\ddot{z}\\ V&=\tau~V\qquad\quad\Rightarrow\qquad\quad \Gamma=\tau~\frac{dV}{dt}+n~\frac{V^2}{R}\end{aligned}\]

Le seul mouvement d’accélération nulle est le mouvement rectiligne uniforme. Lorsque la vitesse est discontinue, l’accélération n’existe pas. Lorsque la vitesse est dérivable, l’accélération est bornée. Les deux cas rencontrés dans la pratique sont les mouvements à accélération bornée et les mouvements avec discontinuités de vitesse.

Il peut arriver que la vitesse $V$ d’un point $M$ par rapport à un repère $S_1$ soit connue par ses composantes sur les axes $Oxyz$ d’un trièdre mobile $S$.

En désignant par $\omega$ la rotation de $S$ par rapport à $S_1$, on peut écrire (de ce qui précède) : \[\Gamma=\Big\{\frac{dV}{dt}\Big\}_{S1}=\Big\{\frac{dV}{dt}\Big\}_S+\omega\wedge V \qquad \left\{ \begin{aligned} \Gamma_x=\frac{dV_x}{dt}+q~V_z-r~V_y\\ \Gamma_y=\frac{dV_y}{dt}+r~V_x-p~V_z\\ \Gamma_z=\frac{dV_z}{dt}+p~V_y-q~V_x \end{aligned} \right.\]

6.2. Composition des accélérations

La distribution des accélérations dans le mouvement d’un solide se détermine par dérivation de la relation : \[V=V_0+\omega\wedge OM\]

On obtient : \[\Gamma=\Gamma_0+(\dot{\omega}\wedge OM)+\omega\wedge(\omega\wedge OM)\]

$\dot{\omega}$ désigne l’accélération angulaire qui peut être évaluée indifféremment par rapport au solide ou par rapport à l’espace fixe.

Une méthode physique de calcul

On désigne le repère fixe par $O_1x_1y_1z_1$ et le repère mobile (lié au solide) par $Oxyz$ dont les vecteurs unitaires sont $\vec{i},~\vec{j},~\vec{k}$. Dans le référentiel lié au solide et à l’instant t :

\[\begin{aligned} &\vec{V}_r=\vec{i}~\frac{dx}{dt}+\vec{j}~\frac{dy}{dt}+\vec{k}~\frac{dz}{dt}\\ &\vec{\Gamma}_r=\vec{i}~\frac{d^2x}{dt}+\vec{j}~\frac{d^2y}{dt}+\vec{k}~\frac{d^2z}{dt}\end{aligned}\]

Calculons la vitesse et l’accélération dans le mouvement absolu (par rapport à $O_1x_1y_1z_1$).

Avec $\overrightarrow{O_1M}=\overrightarrow{O_1O}+\overrightarrow{OM}$ :

\[\begin{aligned} &\overrightarrow{V}_a=\frac{d}{dt}(\overrightarrow{O_1M})\\ &\overrightarrow{\Gamma}_a=\frac{d^2}{dt^2}(\overrightarrow{O_1M})\end{aligned}\]

En dérivant :

\[\begin{aligned} \overrightarrow{V_a}&=\overrightarrow{V}_{O_1}+\frac{d}{dt}(x\vec{i}+y\vec{j}+z\vec{k})\\ \overrightarrow{V_a}&=\overrightarrow{V_{O_1}}+x~\frac{d\vec{i}}{dt}+y~\frac{d\vec{j}}{dt}+z~\frac{d\vec{k}}{dt}\\ \overrightarrow{V_a}&=\overrightarrow{V_e}+\overrightarrow{V_r}\end{aligned}\]

Soit $\overrightarrow{V_e}$ la vitesse d’entrainement, vitesse dans le trièdre $O_1x_1y_1z_1$ du point fixe du référentiel $Oxyz$ (en coïncidence avec le point $M$ à l’instant $t$).

Pour l’accélération : \[\overrightarrow{\Gamma_a}=\overrightarrow{\Gamma_O}+\frac{d^2}{dt^2}(x~\vec{i}+y~\vec{j}+z~\vec{k})=\overrightarrow{\Gamma_a}+\overrightarrow{\Gamma_e}+\overrightarrow{\Gamma_c}\]

avec :

\[\begin{aligned} &\overrightarrow{\Gamma}_e=\overrightarrow{\Gamma}_O+x~\frac{d^2\vec{i}}{dt^2}+y~\frac{d^2\vec{j}}{dt^2}+z~\frac{d^2\vec{k}}{dt^2} &&\text{accélération d’entrainement}\\ &\overrightarrow{\Gamma}_c=2~\Big\{\frac{dx}{dt}~\frac{d\vec{i}}{dt}+\frac{dy}{dt}~\frac{d\vec{j}}{dt}+\frac{dz}{dt}~\frac{d\vec{k}}{dt}\Big\} &&\text{accélération complémentaire}\end{aligned}\]

Sachant que : \[\frac{d\vec{i}}{dt}=\vec{\omega}\wedge\vec{i}\quad;\quad\dots\]

Il vient : \[\overrightarrow{\Gamma_c}=2~\overrightarrow{\omega}\wedge\Big\{\vec{i}~\frac{dx}{dt}+\vec{j}~\frac{dy}{dt}+\vec{k}~\frac{dz}{dt}\Big\}=2~\overrightarrow{\omega}\wedge\overrightarrow{V_r}\]

En définitive : \[\overrightarrow{\gamma_a}=\overrightarrow{\Gamma}_r+\overrightarrow{\Gamma_e}+2~\overrightarrow{\omega}\wedge\overrightarrow{V_r}\]

Actualisé le 2014-03-29

↑ Haut

III. Éléments de cinématique. Vitesses et accélérations

Plan du site

1. Définition de la vitesse