1. Retour sur la notion d’indépendance

On a vu que pour que deux variables soient indépendantes, il faut et il suffit que :

\[\begin{aligned} p_{ij}&=p_i~p_j \qquad \forall i,j &&\text{dans le cas de variables discrètes}\\ f(x,y)&=f_x(x)~f_y(y) &&\text{dans le cas de variables continues}\end{aligned}\]

Il s’ensuit que : \[\text{$X$ et $Y$ indépendantes}\quad\Rightarrow\quad E(XY)=E(X)~E(Y)\]

Cependant, l’implication réciproque est fausse, ce que l’on mettra en évidence avec le contre-exemple qui suit : \[\begin{matrix} &Y~\backslash~X&|&-2&-1&0&1&2&|&p_{\bullet j}\\ \hline &2&|&0.2&0&0&0&0.2&|&0.4\\ &-1&|&0&0.2&0&0.2&0&|&0.4\\ &-2&|&0&0&0.2&0&0&|&0.2\\ \hline &p_{i\bullet}&|&0.2&0.2&0.2&0.2&0.2&|&1 \end{matrix}\] Remarque

On notera la présence d’une ligne et d’une colonne supplémentaires. Elles correspondent respectivement aux probabilités marginales rapportées de \(X\) et \(Y\) c’est-à-dire \(p_{i\bullet}\) et \(p_{\bullet j}\). Le dernier élément (unité) correspondant à la somme de ces probabilités respectives (axiome des probabilités totales).

On peut en effet vérifier que : \[\overline{X}=0 \quad ; \quad \overline{Y}=0 \quad ; \quad \overline{X}~\overline{Y}=0 \quad ; \quad \overline{XY}=0\]

On pourrait donc dire que : \[\overline{X}~\overline{Y}=\overline{XY}=0\]

Cependant, on pourrait vérifier que : \[Y=X^2-2\]

Il existe donc une relation entre \(X\) et \(Y\), c’est-à-dire qu’il existe dans le tableau des probabilités un élément au moins tel que \(p_{ij}\neq p_i~p_j\).

Le premier élément du tableau en fournit la preuve : \(0.2\neq 0.4\times 0.2\).

2. Coefficient de corrélation

Introduisons les variables suivantes :

La variance : \[\sigma_x^2=E{(X-\overline{X})}^2 \quad ; \quad \sigma_x^2=E{(Y-\overline{Y})}^2\]

La covariance : \[\sigma_{xy}=E\{(X-\overline{X})(Y-\overline{Y})\}\]

Une variable auxiliaire : \[Z=aX+Y \qquad a\in\mathbb{R}\]

Expression de l’écart à la moyenne : \[Z-\overline{Z}=a(X-\overline{X})+(Y-\overline{Y})\]

Expression de la variance : \[\sigma_z^2=E\{{(Z-\overline{Z})}^2\}=E\{a^2{(X-\overline{X})}^2+{(Y-\overline{Y})}^2+(X-\overline{X})(Y-\overline{Y})\}\]

On a ainsi :

\[\begin{aligned} Z&=aX+Y\\ \sigma_z^2&=a^2~\sigma_x^2+2a~\sigma_{xy}+\sigma_y^2\end{aligned}\]

Le trinôme en \(a\) est positif ou nul. Son discriminant est donc négatif ou nul (inégalité de Schwartz) : \[\sigma_{xy}^2\leq\sigma_x^2~\sigma_y^2\]

Cette relation suggère l’introduction d’un coefficient \(r\), sans dimension, appelé coefficient de corrélation de \(X\) et \(Y\) défini par : \[r^2=\frac{\sigma_{xy}^2}{\sigma_x~\sigma y} \qquad\ |r|<1\]

Ou encore : \[r=\frac{E\{(X-\overline{X})(Y-\overline{Y})\}}{\sqrt{E\big\{{(X-\overline{X})}^2\big\}}~\sqrt{E\big\{{(Y-\overline{Y})}^2\big\}}}\]

3. Corrélation et indépendance

3.1. Théorème 1

Si les variables \(X\) et \(Y\) sont indépendantes, alors \(r=0\) et \(X\) et \(Y\) ne sont pas corrélées.

En effet : \[\sigma_{xy}=E(X-\overline{X})~E(Y-\overline{Y})=0 \qquad \text{les variables étant centrées}\]

Mais la réciproque est fausse, ce que l’on peut voir sur un contre-exemple :

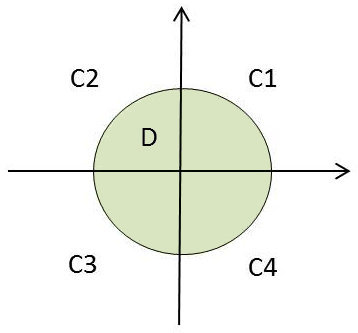On considère le couple de variables \((X,Y)\) uniformément réparties sur un disque de rayon \(R\). On suppose par exemple que (homogénéité pour la dimension 2, équivalent de la linéarité pour la dimension 1) :

\[\begin{aligned} f(x,y)&=\frac{1}{\pi R^2} && x^2+y^2<R^2\\ f(x,y)&=0 && x^2+y^2>R^2\end{aligned}\]

Les variables sont bien dépendantes et de manière explicite puisque \((x^2+y^2) < R^2\).

On va cependant constater que \(r=0\) et, par raison de symétrie, que \(\overline{X}=0\) et \(\overline{Y}=0\).

On a donc : \[\sigma_{xy}=\int\int_D x~y~f(x,y)~dx~dy =0\]

Le résultat est intuitif et sans calcul. On remarque en effet que les intégrations sur les secteurs \(C_i\) donnent des valeurs absolues égales. Cependant :

• Pour \(C_1\) et \(C_3\), on a une fonction intégrée positive.

• Pour \(C_2\) et \(C_4\), on a une fonction intégrée négative.

 
Ainsi \(\sigma_{xy}=0\) et \(r=0\) (c.q.f.d.) : les variables sont dépendantes, mais non corrélées.

3.2. Théorème 2

Pour que \(|r|=1\), il faut et il suffit qu’il existe entre \(X\) et \(Y\) une relation fonctionnelle linéaire.

Si \(|r|=1\), alors le discriminant du trinôme en \(a\) est nul et il existe une racine double \(a_0\) telle que : \[\sigma_z^2=\sigma_x^2~a_0^2+2~\sigma_x~a_0+\sigma_y^2=0\]

C’est-à-dire que : \[E\{{(Z-\overline{Z})}^2\}=0\]

On dira que \(Z\) est une variable certaine, c’est-à-dire que : \[Z=cte \ \ \ et \ \ \ aX+Y=cte\]

En résumé, si \(|r|=1\), les variables \(X\) et \(Y\) sont liées par une relation fonctionnelle linéaire \(Y=aX+b\).

Variable certaine ? Explication

On se place dans le cas discret sans perte de généralité. Reprenons les deux relations :

\[\begin{aligned} \overline{Z}&=m\\ \sigma_z^2&=\sum_i ~p_i~{(z_i-m)}^2=0\end{aligned}\]

Comme \(p_i\geq 0\) et comme il existe au moins un \(p_i\neq 0\), on doit avoir \(z_i=m=cte\).

4. Considérations physiques

Le coefficient de corrélation caractérise non pas une relation quelconque, mais seulement une relation dite linéaire.

On dit que deux variables aléatoires sont liées par une relation probabiliste linéaire si, lorsque l’une d’elles croît, l’autre accuse une tendance à croître ou à décroître suivant une loi linéaire.

Cette tendance linéaire peut être plus ou moins prononcée et s’approcher plus ou moins d’une relation fonctionnelle, c’est-à-dire d’une relation linéaire au sens strict. Le coefficient de corrélation indique à quel point la relation linéaire entre deux variables aléatoires est intime.

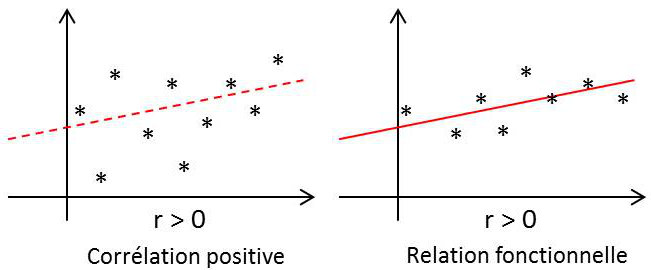
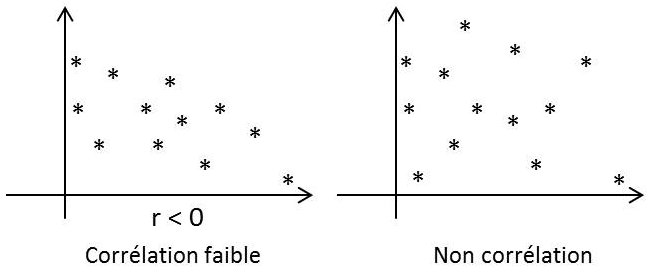Si X et Y sont liées par une relation fonctionnelle exacte : \[Y=aX+b \quad ; \quad r=\pm 1 ~ \text{ suivant le signe de }a\]

Dans le cas général, les variables X et Y sont liées par une relation probabiliste arbitraire \(-1<r<+1\). Les résultats expérimentaux de la figure ci-contre illustrent bien le propos.

5. Étude d’un exemple complet

On considère une variable aléatoire \(t\) prenant, avec une distribution uniforme, toutes les valeurs entre \([0,2\pi]\) . On introduit deux nouvelles variables aléatoires :

\[\begin{aligned} X&=cos(t)\\ Y&=cos(t+\varphi) \qquad \varphi = \text{nombre fixé}\end{aligned}\]

Distribution uniforme sur \([0,2\pi]\) : \[f(t)=\frac{1}{2\pi}\]

Calcul des moyennes :

\[\begin{aligned} E(X)&=\frac{1}{2\pi}\int_0^{2\pi}cos(t)~dt=0\\ E(Y)&=\frac{1}{2\pi}\int_0^{2\pi}cos(t+\varphi)~dt=0\\ E(X^2)&=\frac{1}{2\pi}\int_0^{2\pi}cos^2(t)~dt=\frac{1}{2\pi}\int_0^{2\pi}\frac{1+cos(2t)}{2}~dt=\frac{1}{2}\\ E(Y^2)&=\frac{1}{2}\\ E(XY)&=\frac{1}{2\pi}\int_0^{2\pi}cos(t)~cos(t+\varphi)~dt=\frac{1}{2\pi}\int_0^{2\pi}\frac{cos(\varphi)-cos(2t+\varphi)}{2}~dt=\frac{cos\varphi}{2}\end{aligned}\]

Calcul du coefficient de corrélation (variables centrées : \[r=\frac{E(XY)}{\sqrt{E(X^2)~E(Y^2)}}=\cos \varphi\]

Discussion :

\[\begin{aligned} &\varphi=0 \qquad r=+ 1 \quad \Rightarrow \quad X= Y \\ &\varphi=\pi \qquad r=- 1 \quad \Rightarrow \quad X= -Y\end{aligned}\]

On a donc une relation fonctionnelle linéaire : \[\varphi=(\frac{\pi}{2},\frac{3\pi}{2}) \qquad r=0 \quad \Rightarrow \quad X^2+Y^2=R^2\]

Le point \((X,Y)\) décrit donc un cercle. On obtiendrait une ellipse pour \(\varphi\) quelconque.