1. Caractéristiques de position

1.1. Notion de mode

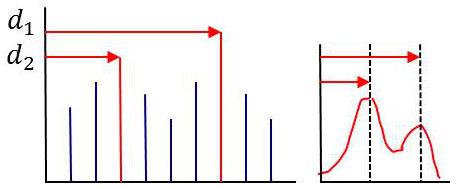On appelle mode la dominante en valeur la plus fréquente. S’il y a deux modes, \(d_1\) sera le mode absolu et \(d_2\) le mode relatif.

Ces définitions s’étendent également aux représentations continues.

1.2. Notion de médiane

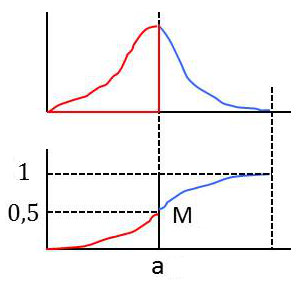Par définition, on désigne par médiane tout nombre \(a\) tel que 50 % au plus de l’effectif total ait un caractère de valeur inférieure à la valeur \(a\).

Pour déterminer graphiquement la médiane \(a\), on utilise le polygone des effectifs cumulés : le point \(M\) est obtenu comme intersection avec la droite d’ordonnée 0,5. On en déduit ensuite \(a\) en traçant une droite verticale passant par \(M\).

Cette méthode graphique s’applique aux variables discrètes et continues.

1.3. Notion de quantile

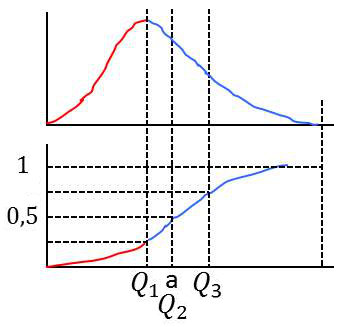Le quantile est une extension de la méthode de la médiane, le partage de la surface se faisant par quart.

À partir des points d’ordonnées 0,25, 0,50 et 0,75, on obtient quatre portions de courbe sur le polygone des effectifs cumulés, puis le partage de l’histogramme.

On remarquera que \(a = Q_2\).

1.4. Notion de moyenne

Dans le calcul des statistiques, on est amené à manipuler trois types de moyennes.

Moyenne arithmétique

Les valeurs \(\{x_1,~x_2,~\dots,~x_p\}\) sont répétées \(n_1\) fois, \(n_2\) fois, etc.

La moyenne arithmétique a pour expression : \[\overline{x}=\frac{\sum_{i=1}^p n_i~x_i}{n}=\sum_i \nu_i~x_i\]

Moyenne géométrique

La moyenne géométrique est définie par : \[G=\sqrt{x_1^{n_1}~x_2^{n_2}~\dots~x_p^{n_p}}\]

Ou encore : \[n~\ln(G)=\sum_i \nu_i~\ln(x_i)\]

Moyenne harmonique

La moyenne harmonique est définie par \(h\) telle que : \[\frac{1}{h}=\frac{n_1}{n}~\frac{1}{x_1}+\cdots+\frac{n_p}{n}~\frac{1}{x_p}=\sum_i\frac{\nu_i}{x_i}\]

2. Caractéristiques de dispersion

2.1. Étendue de la série

L’étendue de la série constitue déjà un renseignement.

2.2. Étendue interquartile

L’écart \(\Delta Q=Q_3-Q_1\) donne l’intervalle des valeurs du caractère à partir de la population, constitué par l’ensemble des deux quarts autre que la médiane.

2.3. Écart moyen

L’écart moyen peut être défini par rapport à \(m\) ou \(a\).

L’écart moyen rapporté à la moyenne sera : \[E_m=\frac{\sum_i n_i~|x_i-m|}{n}=\sum_i\nu_i~|x_i-m|\]

L’écart moyen rapporté à la médiane sera : \[E_a=\frac{\sum_i n_i~|x_i-a|}{n}=\sum_i\nu_i~|x_i-a|\]

2.4. Fluctuation ou variance

Physiquement, la variance a la dimension du carré du caractère : \[\sigma^2=\frac{\sum_i n_i~|x_i-m|^2}{n}\quad >0\]

2.5. Écart type

L’écart type est la valeur de \(\sigma\), avec la dimension du caractère.

3. Coefficient de corrélation

On retrouve les mêmes notions que celles établies en calcul des probabilités. Le coefficient de corrélation entre les deux caractères \(x\) et \(y\) est défini par : \[r=\frac{\sum_i(x_i-\overline{x})~(y_i-\overline{y})}{\sqrt{\sum_i(x_i-\overline{x})^2~(y_i-\overline{y})^2}}\]

Suivant les valeurs de \(r\) :

\[\begin{aligned} &r=\pm 1 &&\text{linéarité}\\ &r=0 &&\text{caractères indépendants}\\ 0<&r<1 &&\text{corrélation positive}\\ -1<&r<0 &&\text{corrélation négative}\end{aligned}\]