1. Introduction
On a défini la transformée de Fourier (TF) d’un signal à temps discret \(x(k)\), écriture condensée (et simplifiée)de \(x(k~T)\) avec \(T=1\), par : \[X(f)=\sum_{k=-\infty}^{+\infty} x(k)~e^{-j~2\pi~f}\]
Cette transformée de Fourier est donc une fonction de la variable continue \(f\) et c’est une fonction périodique de période \(T=1\).
Si on veut mettre en œuvre le calcul de cette TF sur ordinateur on est confronté à deux difficultés :
-
le calcul ne peut se faire qu’à partir d’un nombre fini de valeurs de \(x(k)\) ;
-
le calcul ne peut fournir qu’un nombre fini de valeurs évaluant \(X(f)\) pour des valeurs discrètes de la fréquence.
2. Définition de la transformée de Fourier discrète
À une suite de \(N\) valeurs \(\{x(0),~\dots,~x(n),~\dots,~x(N-1)\}\), la transformée de Fourier discrète (TFD) associe une suite de \(N\) autres valeurs \(\{X(0),~\dots, X(n),~\dots, X(N-1\})\) définies par : \[X(k)=\sum_{n=0}^{N-1} x(n)~\exp(-j~\frac{2\pi~k~n}{N})\qquad k\in[0,~N-1]\]
La TFD est donc une application linéaire qui associe au vecteur \(\{x\}\) le vecteur \(\{X\}\) : \[\{x(0),~\dots,~x(n),~\dots,~x(N-1)\}\quad\xrightarrow{~TFD~}\quad\{X(0),~\dots,~X(n),~\dots,~X(N-1\}\]
En posant :
\[\begin{aligned} &W_N=\exp\Big(-j~\frac{2\pi}{N}\Big)\\ &X(k)=\sum_{n=0}^{N-1} x(n)~W_N^{k~n}\end{aligned}\]
On adopte une écriture matricielle commode : \[\begin{pmatrix} X(0)\\ X(1)\\ \dots\\ X(k)\\ \dots\\ X(N-1) \end{pmatrix} = \begin{pmatrix} 1&1&1&..&1\\ 1&W^1&W^2&..&W^{N-1}\\ \dots&\dots&\dots&\dots&\dots\\ 1&W^k&W^{2~k}&\dots&W^{k~(N-1)}\\ \dots&\dots&\dots&\dots&\dots\\ 1&W^{N-1}&W^{2~(N-1)}&\dots&W^{(N-1)~(N-1)} \end{pmatrix} \times \begin{pmatrix} x(0)\\ x(1)\\ \dots\\ x(k)\\ \dots\\ x(N-1) \end{pmatrix}\]
Pour la transformation TFD inverse : \[x(n)=\frac{1}{N}~\sum_{k=0}^{N-1} X(k)~\exp\Big(j~\frac{2\pi~k~n}{N}\Big)\qquad\forall~n\in[0,~N-1]\]
La démonstration est immédiate en remplaçant \(X (n)\) par son expression donnée en définition.
3. Approximation réalisée par la TFD
En première approximation, il semble que la TFD réalise un échantillonnage du spectre \(X(f)\) du signal \(x(k)\). Ceci n’est rigoureusement exact que si \(x(k)\) est à durée finie [0, N – 1]. Dans le cas contraire, si \(x(k)\) est à durée finie supérieure, voire infinie, la TFD ne fournit que des échantillons du signal tronqué \(x(k)~\Pi_N(k)\).
 Cette troncature brutale du signal peut faire apparaître des oscillations parasites dans le spectre obtenu, ce qui nécessite parfois l’usage de fenêtres de troncature ou de pondération moins brutales (fenêtres triangulaire, de Hamming, de Hanning, etc.)
Cette troncature brutale du signal peut faire apparaître des oscillations parasites dans le spectre obtenu, ce qui nécessite parfois l’usage de fenêtres de troncature ou de pondération moins brutales (fenêtres triangulaire, de Hamming, de Hanning, etc.)
Illustration
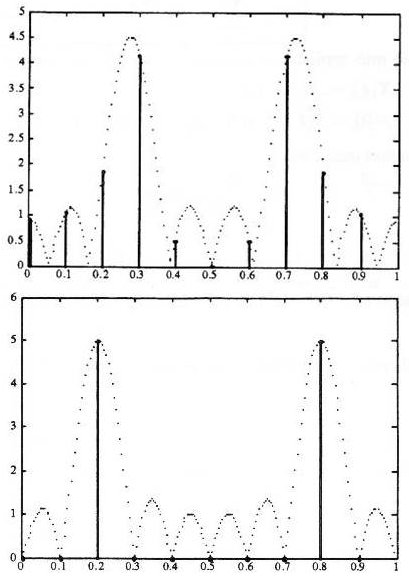
Soit \(x(k)\) résultant de l’échantillonnage d’un signal sinusoïdal de fréquence \(f_0\)et comportant \(N\) points.
La TFD réalise l’échantillonnage du spectre de : \[\cos(2\pi~f_0~k)~\Pi_{NTe}(k)\]
Figure 1 : \[f_0=0,275~f_e\qquad N=10\]
Figure 2 : \[f_0=0,2~f_e\qquad N=10\]
4. Principes des algorithmes rapides
Connu sous la désignation anglosaxonne \(FFT\) (Fast Fourier Transform), l’algorithme rapide se base sur le calcul de la TFD sous la forme : \[X_k=\sum_{n=0}^{N-1}x(n)W_N^{k~n}\qquad\text{avec :}\quad W_N^{k~n}=\exp(-j\frac{2\pi~k~n}{N})\]
Il nécessite \(N^2\) multiplications complexes (ordre de complexité = \(N^2\)).
Un calcul simple montre que pour les indices pairs (\(n=2~p\)) : \[W_N^{2~p~k}=W_{N/2}^{p~k}\]
Et pour les indices impairs (\(n=2~p+1\)) : \[W_N^{(2p+1)~k}=W_{N/2}^{p~k}~W_N^k\]
En séparant les indices pairs et impairs dans la somme précédente : \[X_k=\sum_{n=0}^{(N/2)-1} x(2~n)~W_{N/2}^{k~n}+W_N^k\sum_{n=0}^{(N/2)-1}x(2~n+1)~W_{N/2}^{k~n}\]
Chacune des T...FD nécessitant \(N^2/4\) multiplications complexes, le calcul complet effectué sous cette forme n’en nécessite plus que \(N^2/2\).
On remarque que le processus peut être réitéré autant de fois que l’on veut à la condition que N soit une puissance de 2. Le gain en temps de calcul est alors extrêmement appréciable.

