1. Cas général

Dans ce chapitre, nous n’insisterons que sur les notions simples qui conduiront aux points essentiels, c’est-à-dire les séries de Taylor et les séries de Laurent qui conduiront à leur tour au calcul des résidus, donc des intégrales définies.

1.1. Définition

Soit un ensemble de fonctions holomorphes dans un domaine fermé \(D\) : \[u_1(z),~u_2(z),~u_3(z),~\dots,~u_n(z)\dots\]

La somme \(S=\sum u_n(z)\) est uniformément convergente dans \(D\) si, étant donné \(\varepsilon>0\), il existe un entier \(N(\varepsilon)\) tel que : \[|R_n(z)|<\varepsilon\quad\text{pour}\quad n > N\]

\(R\) désignant le reste des termes de la série à partir du rang \(n\).

1.2. Quelques règles

Considérons une série numérique à termes positifs \(v_i\) convergente. Alors : \[|u_n|<v_n~~\forall n\quad\Rightarrow\quad S~\text{uniformément convergente}\]

Comme dans le cas réel, une somme de fonctions continues est une fonction continue.

Comme dans le cas réel, les théorèmes sur la dérivation et sur l’intégration s’appliquent.

1.3. Théorème

Nous énoncerons ce théorème, spécifique aux fonctions holomorphes, sans démonstration :

Si la série est uniformément convergente sur la frontière de \(D\), si les fonctions \(u_n(z)\) sont holomorphes sur \(D\), la somme \(S(z)\) de la série est elle-même holomorphe à l’intérieur de \(D\).

2. Séries entières

Les séries entières sont de la forme : \[\sum_{n=1}^{\infty} a_n~z_n\qquad (a_n,~z)\in C\]

2.1. Lemme d’Abel

Si une série converge pour \(z=z_0\), elle converge en module : \[\forall z\quad |z|<|z_0|\]

2.2. Convergence uniforme

Toute série entière est uniformément convergente à l’intérieur de son cercle de convergence.

Remarque

Si l’on considère un cercle \(\Gamma\) intérieur au cercle de convergence, \(\sum a_n~z_n\) est uniformément convergente sur \(\Gamma\). À l’intérieur de \(\Gamma\), les fonctions \(a_n~z_n\) sont holomorphes.

Ainsi, à l’intérieur du cercle de convergence, une série entière est une fonction holomorphe. On peut donc dériver ou intégrer sur n’importe quel chemin à l’intérieur du cercle de convergence.

Exemples

Soit la série : \[f(z)=1+\frac{z}{1!}+\frac{z^2}{2!}+\cdots+\frac{z^n}{n!}+\cdots\]

Il est évident que : \[f'(z)=f(z)\]

Par suite : \[f(z)=c~e^z=e^z\qquad\text{car :}\quad f(0)=1\]

Les séries \(\sin(z),~\cos(z),~\sinh(z),~\cosh(z)\) convergent aussi dans le plan complexe : \[f(z)=\sum_{n=0}^{\infty}\frac{z^n}{n!}\qquad;\qquad f(i~z)=\sum_{n=0}^{\infty}\frac{(i~z)^n}{n!}\]

On en déduit les formules classiques :

\[\begin{aligned} \cos(z)=\sum_{p=0}^{\infty}(-1)^p~\frac{z^{2~p}}{(2~p)!}\qquad&;\qquad \sin(z)=\sum_{p=0}^{\infty}(-1)^p~\frac{z^{2~p+1}}{(2~p+1)!}\\ \cosh(z)=\sum_{p=0}^{\infty}\frac{z^{2~p}}{(2~p)!}\qquad&;\qquad \sinh(z)=\sum_{p=0}^{\infty}\frac{z^{2~p+1}}{(2~p+1)!}\end{aligned}\]

3. Séries de Taylor

Nous savons que toute série entière dans son cercle de convergence est une fonction holomorphe. Une fonction holomorphe est-elle développable en série entière ?

On démontre (développement de Taylor) qu’au voisinage d’un point \(a\) donné et sur un cercle \(C\) de centre \(a\) :

\[\begin{aligned} &f(z)=f(a)+\frac{(z-a)}{1!}~f'(a)+\frac{(z-a)^2}{2!}~f''(a)+\cdots+\frac{(z-a)^n}{n!}~f^{(n)}(a)+\cdots \\ &f'(a)=\frac{1}{2~i~\pi}\int_C\frac{f(s)~ds}{(s-a)}\quad;~\cdots~;\quad f^{(n)}(a)=\frac{n!}{2~i~\pi}\int_C\frac{f(s)~ds}{(s-a)^{n+1}}\end{aligned}\]

4. Séries de Laurent

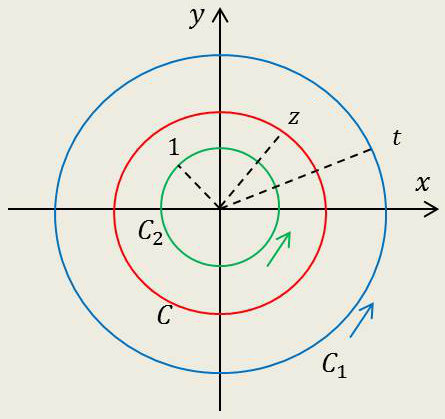Supposons que \(f(z)\) admette l’origine comme point singulier non critique. On ne peut faire de développement de Taylor en 0, car la fonction n’y est pas holomorphe, mais elle l’est dans une couronne délimitée par les cercles \(C_1\) et \(C_2\).

On démontre (développement de Laurent) que : \[f(z)=\cdots+\frac{b_n}{z^n}+\cdots+\frac{b_1}{z}+a_0+a_1~z+\cdots+a_n~z^n+\cdots\]

C’est-à-dire : \[f(z)=\sum_{n=-\infty}^{n=+\infty} a_n~z^n\]

avec : \[a_n=\frac{1}{2~i~\pi}\int_C\frac{f(t)~dt}{t^{n+1}}\qquad;\qquad b_n=a_{(-n)}\]