1. Production
Comment fournir l’énergie nécessaire pour arracher un ou plusieurs électrons de l’atome ou de la molécule neutre ? On y parvient de plusieurs façons :
-
par effet photoélectrique (toute l’énergie du photon est utilisée) ;
-
par rayonnement ionisant \(X,\alpha,\beta,\gamma\) (utilisation d’une faible partie de l’énergie des particules) ;
-
par chocs atomiques ou ioniques dirigés (faisceau atomique, oscillations HF) ;
-
par chocs thermiques : à la température \(T\) dans un gaz parfait, une certaine proportion des particules de l’ordre de \(\exp(-W/k~T)\) a une énergie supérieure à \(W\) (de l’ordre de \(10^{-4,3}\) pour une température de 1200 K et pour une énergie de 1 eV ;
-
par réaction chimique, combustion
-
par un fort champ électrique.
On notera que dans un vase clos à l’abri de tout rayonnement, l’agitation thermique crée dans les conditions normales de température et de pression : \[n=6\times 10^{23}~\exp\Big(\frac{-e~V_i}{k~T_0}\Big)~\text{ions/litre}\]
Ainsi, pour \(V_i=1\) V : \[n\approx\frac{6\times 10^{23}}{2\times 10^4}\exp(-40)\approx 100~\text{ions/cm}^3\]
2. Courant d’ionisation à pression ambiante
2.1. Étude du comportement d’une chambre d’ionisation
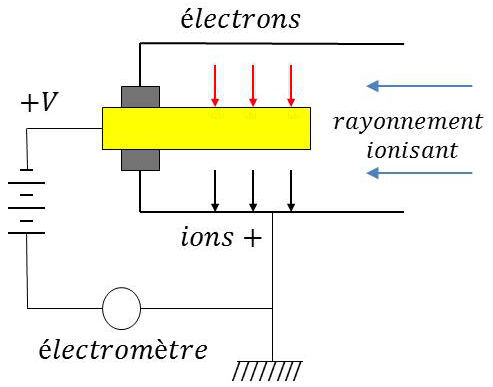 Un flux constant de particules ionisantes pénètre entre deux électrodes soumises à une d.d.p. pouvant varier de 0 à quelques centaines de volts.
Un flux constant de particules ionisantes pénètre entre deux électrodes soumises à une d.d.p. pouvant varier de 0 à quelques centaines de volts.
Le gaz entre les électrodes se trouve à une pression de l’ordre de grandeur de la pression atmosphérique.
Quelques molécules de ce gaz sont ionisées et les ions et les électrons sont attirés par les électrodes.
2.2. Étude du comportement du courant en fonction de la tension appliquée.
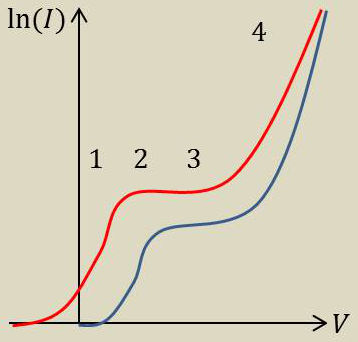 Augmentons progressivement la tension appliquée aux bornes des électrodes d’une chambre d’ionisation :
Augmentons progressivement la tension appliquée aux bornes des électrodes d’une chambre d’ionisation :
-
Aux faibles tensions, une partie croissante des ions formés est recueillie.
-
Sur une certaine gamme de tensions (quelques centaines de volts) pour les chambres d’une centaine de picofarads, le courant ne varie pratiquement pas.
Ce palier signifie que l’on recueille tous les ions formés. Quelques photons X par seconde créent 105 électrons, soit un courant de \(10^{-14}\) A.
-
Pour des tensions plus élevées, le courant croit à nouveau, car les ions accélérés par le champ électrique ionisent à leur tour d’autres molécules par choc.
On désigne par \(l\) le libre parcours moyen (distance parcourue entre deux chocs). Sur ce parcours, l’ion (ou l’électron) acquiert une énergie cinétique supplémentaire : \[\Delta E_c=e~(E~l)=e~\Delta V\]
Le libre parcours moyen des ions est de l’ordre du micromètre dans les conditions normales.
Le gain sera donc de 1 eV pour un champ de 10 kV/cm.
Dans cette région, le courant obtenu pour une valeur donnée de \(V\) est proportionnel au flux incident. Les compteurs dits proportionnels travaillent dans ces conditions.
-
Le champ atteint ensuite une valeur telle qu’une seule particule ionisante allume par avalanche tout le tube : on a atteint le potentiel disruptif. Les compteurs Geiger travaillent dans ces conditions.
L’avalanche charge négativement le conducteur central (les électrons légers arrivent avant les ions).
La capacité du compteur étant faible, sa d.d.p. aux bornes chute brutalement de quelques volts et peut actionner, après amplification, un dispositif numérateur.
Le gaz contient des impuretés dont le rôle est d’arrêter rapidement la multiplication des ions après la passage de la particule ionisante : le compteur est prêt à enregistrer le passage d’une nouvelle particule \(10^{-4}\) secondes après (ce qui est souvent insuffisant).
3. Conduction aux basses températures
3.1. Allure de la décharge
Les tubes à décharge conduisent notablement lorsque le potentiel disruptif est atteint. Celui-ci dépend de la pression, l’allure de la décharge également.
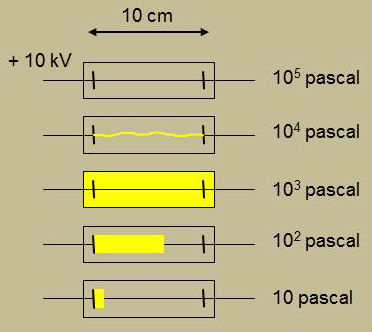 La lumière émise par le gaz provient de la désexcitation ou de la recombinaison des ions, son spectre est caractéristique du gaz.
La lumière émise par le gaz provient de la désexcitation ou de la recombinaison des ions, son spectre est caractéristique du gaz.
Ces tubes sont utilisés pour :
-
l’analyse spectroscopique ;
-
l’éclairage (rendement supérieur à celui des lampes à incandescence) ;
-
la détection des fuites ;
-
les thyratrons (la conduction est commandée par une grille).
D’autre part, en mesurant le courant en-dessous de la décharge, on peut mesurer les pressions inférieures à 10 pascals (jauges à ionisation).
Lorsque le libre parcours moyen des ions et des électrons atteint le centimètre (vers \(10^{-4}\) atmosphères, soit 10 Pa), les ions positifs tombent sur la cathode avec une énergie de plusieurs centaines d’eV. Ils arrachent alors plusieurs électrons qui sont repoussés normalement de la cathode. Ce sont les rayons cathodiques qui, tombant sur le verre, y excitent une lumière verte.
3.2. Loi de Paschen
Pour des électrodes de forme donnée, le potentiel disruptif \(V_C\) ne dépend que du produit \(p~d\) de la pression par la distance des électrodes.
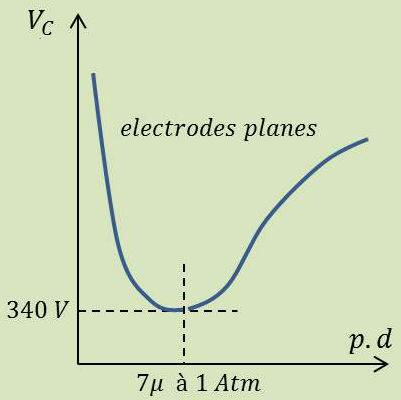 La fonction \(V_C = f(p~d)\) passe par un minimum lorsque \(d\) est de l’ordre de quelques parcours moyens à la pression \(p\).
La fonction \(V_C = f(p~d)\) passe par un minimum lorsque \(d\) est de l’ordre de quelques parcours moyens à la pression \(p\).
Cette propriété s’explique aisément dans les deux régions extrêmes situées de part et d’autre du minimum.
Pour les grandes valeurs de \(p~d \), l’avalanche se produit lorsque le gain moyen d’énergie acquis entre deux chocs atteint une certaine fraction \(\alpha\) de l’énergie d’ionisation \(E_i\) du gaz, soit : \[e~V_c~\frac{l}{d}=\alpha~E_i\]
Or, \(l\) est inversement proportionnel à la pression \(p\).
Aux très basses pressions, lorsque le libre parcours moyen \(l\) est supérieur à la distance \(d\) des électrodes, le nombre de chocs est plus faible, d’autant plus que \(l\) est grand, c’est-à-dire que \(p\) est petite. \(V_c\) ne dépend alors que de la probabilité de choc. Celle-ci varie comme le nombre d’atomes présents dans une tranche de section unité, soit proportionnelle à \(p~d\).
3.3. Expérience de Franck et Hertz
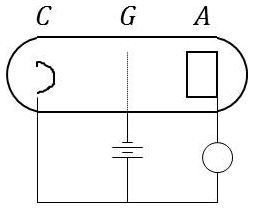 Dans une triode, le tube contient du gaz raréfié.
Dans une triode, le tube contient du gaz raréfié.
La cathode C émet des électrons qui sont accélérés par la grille G.
Dans l’espace grille – plaque, ces électrons heurtent des atomes de gaz qu’ils ionisent si leur énergie est suffisante.
L’ionisation est détectée par un accroissement du courant plaque.
On a pu mesurer ainsi l’énergie d’ionisation \(E_i\) des différents gaz et vérifier que \(E_i\) est relié à la fréquence de seuil \(\nu_s\) de l’effet photoélectrique par : \[E_i=h~\nu_s\]
Dans un thyratron, la pénétration des électrons dans l’espace grille – plaque est bloquée ou non selon le potentiel de la grille. Mais pour bloquer de nouveau un thyratron allumé, il est nécessaire de baisser la tension plaque.
4. Conductibilité des gaz
Nous allons calculer la conductibilité par électron \(C_e\) aux champs faibles, lorsque l’ionisation en chaîne ne se produit pas : \[C_e=n~e~\langle V_e\rangle=\sigma_e~E\]
-
\(n\) : nombre d’électrons par unité de volume
-
\(\langle V_e\rangle\) : vitesse moyenne d’ensemble des électrons
-
\(\sigma_e\) : conductibilité électronique
Or, sous l’action du champ électrique \(E\), l’électron subit un accroissement de vitesse entre deux chocs (durée \(\Delta t_e\)) : \[\Delta V_e=\frac{e}{m}~E~\Delta t_e\]
Seul cet accroissement contribue à la vitesse d’ensemble : \[V_e=\langle\Delta V_e\rangle=\frac{e}{m}~E~\tau_e\quad;\quad\tau_e=\langle\Delta V_e\rangle\]
Finalement : \[\sigma_e=n~\frac{e^2}{m}~\tau_e\]
Dans les conditions normales : \[n=10^8~\text{élecrons/m}^3\quad;\quad\tau_e=10^{-11}\quad;\quad\sigma_e=3\times 10^{-11}~\Omega/\rm m\]
Mobilité des électrons : \[\mu_e=\frac{\langle V_e\rangle}{E}=\frac{e~\tau_e}{m}\approx 2~\rm m^2~V^{-1}~s^{-1}\]
Mobilité des ions : \[\mu_i=Z_i~\frac{e}{M}~\tau_i\]
Si les libres parcours moyens sont comparables, l’équirépartition des énergies cinétiques donne : \[m~v_e^2=M~v_i^2\]
Ce qui entraîne : \[\frac{\tau_i}{\tau_e}=\sqrt{\frac{M}{m}}\quad\Rightarrow\quad\mu_i=\mu_e~\sqrt{\frac{m}{M}}\]
donc 200 fois plus faible.

