1. Courants linéaires

1.1. Courant rectiligne indéfini

Exemple simple de calcul des champs qui permet de comparer les méthodes principales.

1.1.1. Induction par la formule de Biot et Savart

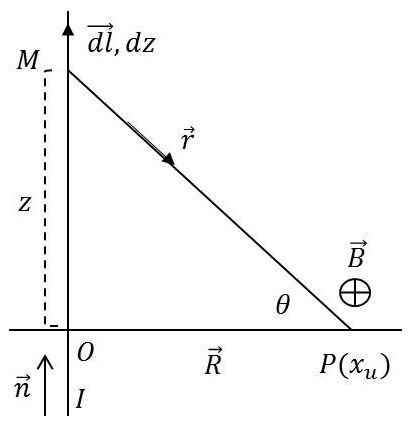Rappelons la formule générale : \[B=\frac{\mu_0~I}{4\pi}\int_C\overrightarrow{dl}\wedge\frac{\overrightarrow{r}}{r^3}\qquad[1]\]

Conformément à la règle du produit vectoriel des éléments d’intégration, l’induction élémentaire sera normale au plan de la figure et dirigée d’avant en arrière.

En écrivant que : \[\overrightarrow{dl}\wedge\frac{\overrightarrow{r}}{r^3}=\frac{\cos\theta}{r^2}~dz=\frac{\cos\theta}{R}~d\theta\]

Par suite : \[B=\frac{\mu_0~I}{4\pi~R}\int_{-\pi/2}^{+\pi/2}\cos\theta~d\theta=\frac{\mu_0~I}{2\pi~R}\qquad[2]\]

Et \(\overrightarrow{n}\) étant le vecteur unitaire de la direction du courant : \[\overrightarrow{B}=\frac{\mu_0~I}{2\pi~R}~\Big(\overrightarrow{n}\wedge\frac{\overrightarrow{R}}{R}\Big)\qquad[3]\]

1.1.2. Induction déduite du potentiel vecteur

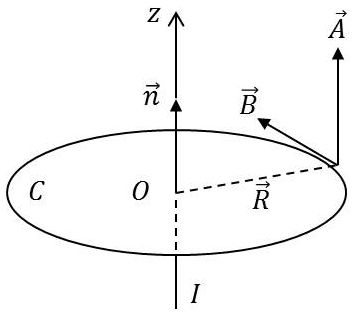L’expression du potentiel-vecteur pour un courant linéaire est connue : \[\overrightarrow{A}=-\frac{\mu_0~I}{2\pi}~\overrightarrow{n}~\ln(R)\quad;\quad R=\sqrt{x_1^2+x_2^2}\qquad[4]\]

En appliquant : \[\begin{aligned} &\overrightarrow{B}=\overrightarrow{\rm rot}\overrightarrow{A}\\ &B_w=\partial_u~A_v-\partial_v~A_u \end{aligned} \qquad[5]\]

Il vient : \[B_z=-\frac{\mu_0~I}{2\pi}~\Big(\frac{R_u}{R^2}~\overrightarrow{n_y}-\frac{R_v}{R^2}~\overrightarrow{n_x}\Big)\qquad[6]\]

formule identique à la précédente.

1.1.3. Induction déduite du théorème d’Ampère

La formule de Biot et Savart montre que \(\overrightarrow{B}\) est tangent à la circonférence \(C\) de rayon \(R\).

On écrit que la circulation du vecteur \(\overrightarrow{H}\) le long de \(C\) est égal à \(I\) et on obtient : \[\begin{aligned} 2\pi~R~H&=I\quad\Rightarrow\quad H=\frac{I}{2\pi~R}\\ B&=\mu_0~H=\frac{\mu_0~I}{2\pi~R} \end{aligned} \qquad[7]\]

1.2. Courant angulaire

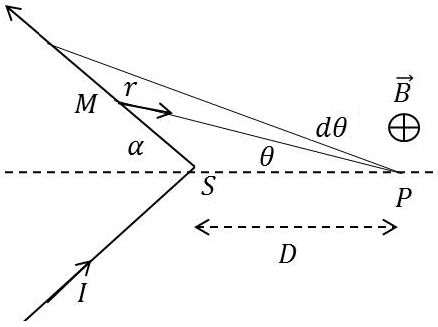Appliquons la formule de Biot et Savart.

Les champs élémentaires sont normaux au plan de la feuille et dirigés vers l’arrière. En valeur absolue : \[dB=\frac{\mu_0~I}{4\pi~r}~d\theta\qquad[8]\]

Dans le triangle \(MSP\) : \[\frac{r}{\sin\alpha}=\frac{D}{\sin(\alpha-\theta)}\]

D’où : \[B=\frac{\mu_0~I}{2\pi~D}~\frac{1}{\sin\alpha}\int_0^{\alpha}sin(\alpha-\theta)~d\theta=\frac{\mu_0~I}{2\pi~D}~\frac{1-\cos\alpha}{\sin\alpha}\]

Tous calculs faits : \[B=\frac{\mu_0~I}{2\pi~D}~\tan\frac{\alpha}{2}\qquad[9]\]

Pour \(\alpha=\cfrac{\pi}{2}\) , on retrouve l’expression obtenue pour le fil rectiligne indéfini.

1.3. Courant circulaire (champ en un point de l’axe)

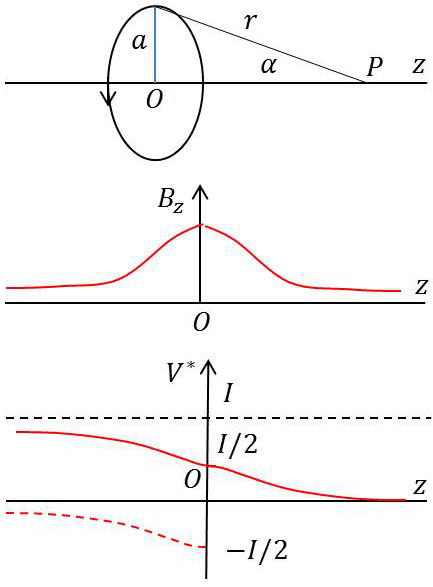L’angle solide (voir appendice) sous lequel du point \(P\), on voit la surface du cercle \(C\) est : \[\Omega=2\pi~(1-\cos\alpha)\qquad[10]\]

Le potentiel scalaire \(V^*\) est donc : \[\begin{aligned} V^*&=\frac{\Omega}{4\pi}=\frac{1}{2}~(1-\cos\alpha)=\frac{1}{2}~\Big(1-\frac{z}{r}\Big)\\ r&=\sqrt{z^2+r^2}\quad;\quad\frac{\partial z}{\partial r}=\frac{z}{r} \end{aligned} \qquad[11]\]

La composante \(H\), dans la direction de l’axe se déduit du potentiel \(V^*\) par : \[\begin{aligned} H_z&=-\frac{\partial V^*}{\partial z}=-\frac{1}{2}~\Big(-\frac{1}{r}+\frac{z}{r^2}~\frac{z}{r}\Big)\\ H_z&=\frac{I~a^2}{2~r^3}=\frac{I}{2~a}~\sin^3\alpha \end{aligned} \qquad[12]\]

Cas particulier : \(P\) est en \(O\) : \[r~\rightarrow a\quad;\quad H_0=\frac{I}{2~a}\quad;\quad B_0=\frac{\mu_0~I}{2~a}\]

Les composantes \(H_x\) et \(H_y\) sont nulles sur l’axe comme on peut s’en rendre compte en utilisant la formule de Biot et Savart et en associant les éléments du courant deux à deux, d’une manière symétrique.

2. Distributions superficielles

2.1. Densité superficielle, potentiel vecteur et induction

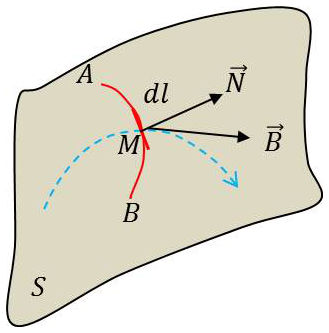Quand des courants circulent sur une surface \(S\), on leur associe une densité superficielle \(\overrightarrow{k}\) de courant.

Si \(dl\) est l’élément d’arc d’une courbe tracée sur la surface, la quantité d’électricité \(dQ\) qui traverse pendant le temps \(dt\) l’élément \(dl\) est, par définition de \(\overrightarrow{k}\) : \[dQ=(\overrightarrow{k}\cdot\overrightarrow{N})~dl~dt\qquad[13]\]

Par analogie avec la densité volumique \(\rho\) : \(\overrightarrow{i}=\rho~\overrightarrow{v}\), on aura une densité superficielle \(\sigma\) telle que \(\overrightarrow{k}=\sigma~\overrightarrow{v}\).

Le potentiel-vecteur et l’induction d’une distribution superficielle sont alors : \[\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_S\frac{\overrightarrow{k}}{r}~dS\quad;\quad\overrightarrow{B}=\frac{\mu_0}{4\pi}\int_S\Big(\overrightarrow{k}\wedge\frac{\overrightarrow{r}}{r^3}\Big)~dS\qquad[14]\]

2.2. Exemple d’une nappe de courant de largeur finie

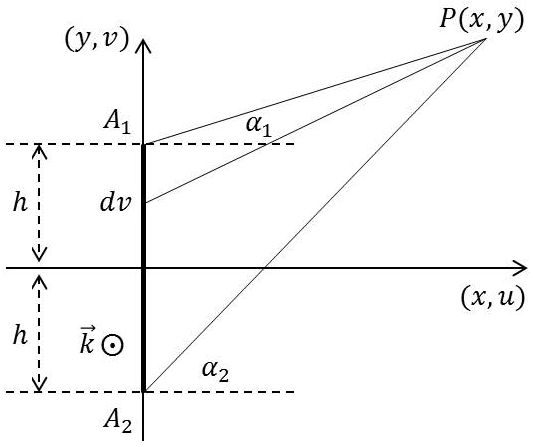Les lignes de courant sont normales au plan de la feuille et dirigées d’avant en arrière. Elles s’étendent sur une largeur \(2~h\).

Si \(I\) est l’intensité totale on a pour la densité superficielle : \[k_z=\frac{I}{2~h}\qquad[15]\]

En vertu de l’expression du potentiel vecteur d’un courant rectiligne, le potentiel vecteur a pour expression : \[\begin{aligned} &A_z=-\frac{\mu_0~k_z}{2\pi}\int_{v=-h}^{v=+h}\ln(R)~dv\\ &R=\sqrt{x^2+(y-v)^2} \end{aligned} \qquad[16]\]

L’intégration est facilitée par le changement de variable : \(\omega=y-v\). Tous calculs faits : \[A_z=\frac{\mu}{2\pi}~\frac{I}{2~h}~\Big\{(y-h)~\ln\frac{R_1}{h}-(y+h)~\ln\frac{R_2}{h}+x~(\alpha_1-\alpha_2)\Big\}\qquad[16]\]

Du potentiel, on en déduit l’induction : \[\begin{aligned} &B_x=\frac{\partial A_z}{\partial y}=-\frac{\mu}{2\pi}~\frac{I}{2h}~\ln\frac{R_2}{R_1}\\ &B_y=\frac{\partial A_z}{\partial x}=-\frac{\mu}{2\pi}~\frac{I}{2h}~(\alpha_2-\alpha_1) \end{aligned} \qquad[17]\]

2.3. Courants sur un cylindre indéfini

Nous allons considérer le cas d’un cylindre avec un type de distribution \(k=cte\), le vecteur courant étant dirigé suivant les génératrices du cylindre.

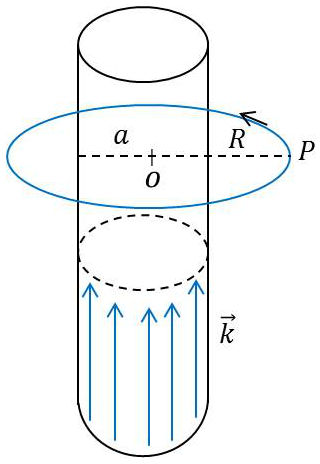L’intensité totale à travers une surface \(S\) est par définition la quantité totale d’électricité qui passe à travers \(S\) pendant une seconde : \[\mathcal{Q}=\int_S(\overrightarrow{n}.\overrightarrow{i})~dS\qquad[18]\]

Le potentiel vecteur pour un courant linéaire (cf. courant rectiligne indéfini) a pour expression : \[\overrightarrow{A}=-\frac{\mu_0~I}{2\pi}~\overrightarrow{n}~\ln(R)\qquad[19]\]

De l’intégration des équations : \[\rm div(\overrightarrow{B})=0\quad;\quad\overrightarrow{\rm rot}\overrightarrow{H}=\overrightarrow{i}\]

Il vient (continuité du champ et de l’induction) à la traversée d’une nappe de courant : \[\begin{aligned} \overrightarrow{n}\cdot(\overrightarrow{B'}-\overrightarrow{B''})&=0\\ \overrightarrow{n}\wedge(\overrightarrow{H'}-\overrightarrow{H''})&=\overrightarrow{k} \end{aligned} \qquad[20]\]

Le potentiel vecteur en un point \(P\) est parallèle aux génératrices du cylindre et il ne dépend que de \(R\) par raison de symétrie.

Le champ est donc normal à \(\overrightarrow{OP}=\overrightarrow{R}\) et dans la direction du vecteur \(\overrightarrow{k}\wedge\cfrac{\overrightarrow{R}}{R}\), c’est-à-dire tangent à la circonférence de centre \(O\) et passant par \(P\).

Dans ces conditions, le théorème d’Ampère appliqué à la circonférence de rayon \(R\) donne : \[2\pi~R~H=\mathcal{Q}=2\pi~a~k\quad\Rightarrow\quad H=\frac{a}{R}~k\qquad[21]\]

Le champ est donc le même que celui d’un courant linéaire circulant le long de l’axe du cylindre et dont l’intensité serait : \[I=2\pi~a~k\]

2.4. Disque de Rowland

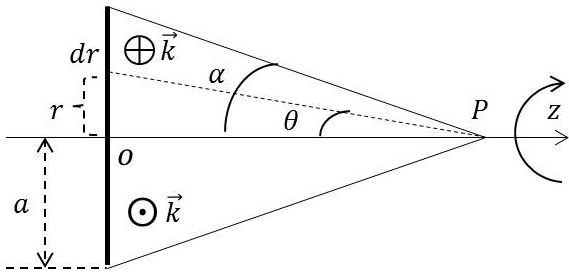On fait tourner un disque métallique portant une densité uniforme \(\sigma\) de charge électrique avec une vitesse angulaire \(\omega\).

On se propose de calculer le champ magnétique en un point de l’axe.

La loi de Biot et Savart donne : \[H_z=\int_0^a\frac{\sin^3\theta}{2r}~k~dr\qquad[22]\]

\(k\) : densité superficielle de courant

On a : \[k=v~\sigma=r~\omega~\sigma\quad;\quad \tan\theta=\frac{r}{z}\]

On doit donc intégrer : \[H_z=\frac{\omega~\sigma}{2}~z\int_0^{\alpha}\frac{\sin^3\theta}{\cos^3\theta}~d\theta=\frac{\omega~\sigma}{2}~z~\Big(\cos\alpha+\frac{1}{\cos\alpha}-2\Big)\qquad[23]\]

Tous calculs faits : \[H_z=\frac{\omega\sigma}{2}~\Big(\frac{2~z^2+a^2}{\sqrt{z^2+a^2}}-2~z\Big)\qquad[24]\]

3. Distributions volumiques

Pour calculer les distributions volumiques, la méthode la plus simple est celle théorème d’Ampère, ainsi que celle du potentiel vecteur.

Par un raisonnement analogue à celui de l’électrostatique, on en déduirait les conditions aux limites pour les potentiels vecteurs : \[(\overrightarrow{A'})_S=(\overrightarrow{A''})_S\quad;\quad\Big(\frac{\partial V'}{\partial n}\Big)_S=\Big(\frac{\partial V''}{\partial n}\Big)_S\qquad[24]\]

Il en résulte que toutes les composantes du champ sont continues à la traversée de la surface limitant une distribution volumique.

3.1. Cylindre indéfini

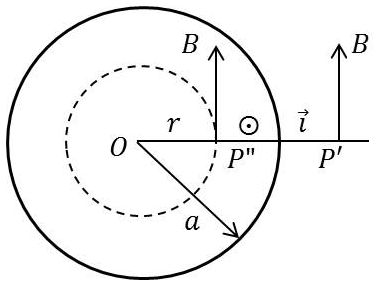Nous supposons que la densité de courant \(\overrightarrow{i}\) est constante et parallèle aux génératrices du cylindre.

Si \(I\) est l’intensité du courant, on a : \[\overrightarrow{i}=\frac{I}{\pi~a^2}~\overrightarrow{n}\qquad[25]\]

\(\overrightarrow{n}\) vecteur unitaire normal au plan, dirigé en avant.

D’après la loi de Biot et Savart, on voit en associant deux à deux les éléments de courant que le champ résultant en un point \(P\) est toujours normal au rayon vecteur \(\overrightarrow{OP}\).

Son sens est toujours donné par le vecteur unitaire \(\overrightarrow{n}\wedge\cfrac{\overrightarrow{r}}{r}\)

En appliquant alors le théorème d’Ampère à la circonférence de rayon \(r\), on a :

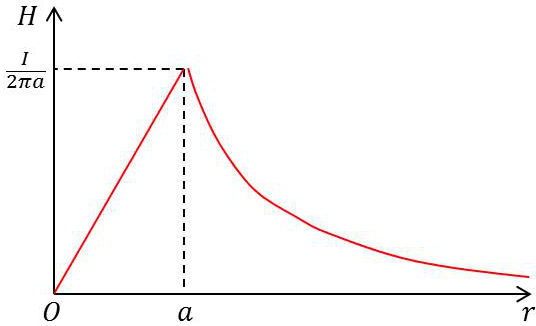À l’intérieur : \[2\pi~r~H''=\frac{\pi~r^2~I}{\pi~a^2}\quad\Rightarrow\quad H=\frac{I~r}{2\pi~a^2}\qquad[26]\]

À l’extérieur : \[2\pi~r~H'=\frac{\pi~a^2~I}{\pi~a^2}\quad\Rightarrow\quad H=\frac{I}{2\pi~r}\qquad[27]\]

La figure indique l’allure de la variation de l’intensité du champ magnétique \(H\) en fonction de \(r\). Quand \(r=a\), on a alors \(H'=H''\) ; les composantes normales sont aussi continues puisqu’elles sont nulles. On peut ensuite calculer le potentiel vecteur \(\overrightarrow{A}\) et en déduire le vecteur induction \(\overrightarrow{B}=\overrightarrow{\rm rot}\overrightarrow{A}\).

3.2. Cylindre creux à symétrie axiale

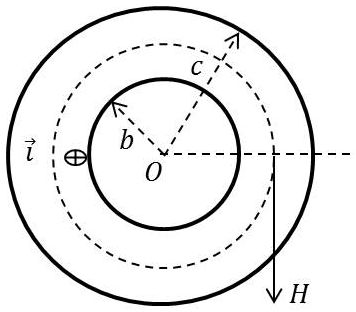Par raison de symétrie, l’induction est toujours normale au rayon vecteur.

Le théorème d’Ampère appliqué à une circonférence de même axe que le cylindre donne :

– Intérieur du cylindre de rayon (\(r=b\)) : \[H_3=0\qquad[28]\]

– Entre les deux cylindres (\(r=b\) et \(r=c\)) : \[2\pi~r~H=i~\pi~(r^2-b^2)\]

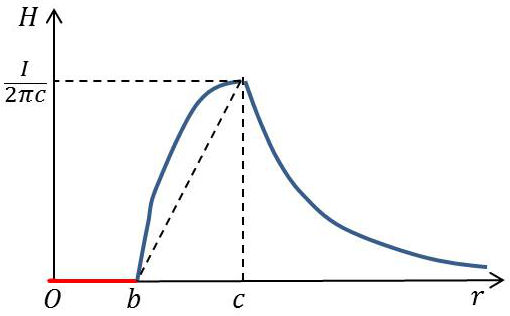Il vient : \[H_2=\frac{i}{2}~\Big(r-\frac{b^2}{r}\Big)=\frac{I}{2\pi~(c^2-b^2)}~\Big(r-\frac{b^2}{r}\Big)\qquad[29]\]

Extérieur du cylindre de rayon (\(r=c\)) : \[2\pi~r~H=i~\pi~(c^2-b^2)\]

Il vient : \[H_1=\frac{i}{2~r}~(c^2-b^2)=\frac{I}{2\pi~r}\qquad[30]\]

On peut ensuite calculer le potentiel vecteur \(\overrightarrow{A}\) et en déduire le vecteur induction \(\overrightarrow{B}=\overrightarrow{\rm rot}\overrightarrow{A}\).

3.3. Câble coaxial

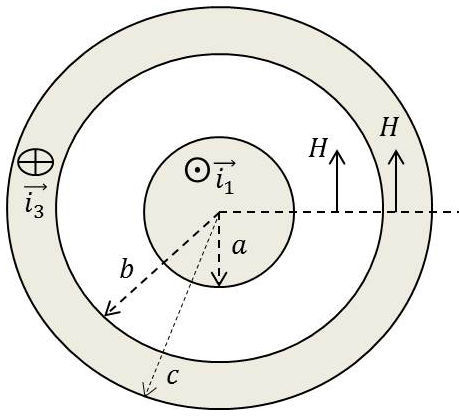Dans le cylindre central le courant circule vers le haut : \[\overrightarrow{i_1}=i_1~\overrightarrow{n}=\frac{I}{\pi~a^2}~\overrightarrow{n}\qquad[31]\]

Dans la partie annulaire, le courant circule vers le bas et l’intensité \(I\) est la même \[\overrightarrow{i_3}=-i_3~\overrightarrow{n}=\frac{I}{\pi~(c^2-b^2)}~\overrightarrow{n}\qquad[32]\]

On obtiendra la solution en additionnant :

• les deux formules de la solution du cylindre plein seul ;

• les formules de la solution pour le cylindre annulaire.

4. Appendice : angle solide

La notion d’angle solide est très pratique pour certains calcul de la physique, dans un espace tridimensionnel. Elle est en fait une généralisation de la notion d’angle, telle que nous la connaissons dans le plan.

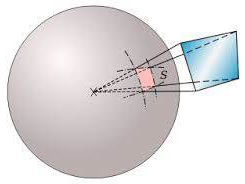L’angle sous lequel on voit un arc de cercle élémentaire (donc très petit) s’exprime par : \[\theta\approx\tan\theta=\frac{ds}{R}\]

Passant en tridimensionnel, le \(ds\) d’arc de cercle est remplacé par le \(dS\), donc surface élémentaire (surface quadrilatère) sur une sphère et le \(R\) par \(R^2\).

Et pour la vison conique d’un disque : \[\Omega=2\pi~(1-\cos\alpha)\]