1. De Bohr à Sommerfeld. Premiers modèles de l’atome
Reprenant le modèle planétaire de Jean Perrin et sans tenir compte des lois de l’électromagnétisme, Bohr a inauguré une physique nouvelle à l’échelle de l’atome en faisant l’hypothèse d’orbites circulaires K, L, M quantifiées. Bohr postulait que : \[mr^2~\omega=n~\frac{h}{2\pi}\qquad\Rightarrow\qquad\omega=\frac{n~h}{2~\pi}~\frac{1}{m~r^2}\]
-
\(n\) : numéro de la trajectoire
-
\(r\) : rayon de la trajectoire
-
\(m\) : masse de la particule
-
\(\omega\) : vitesse angulaire de la particule
L’électron circulant avec la vitesse : \[v=\omega~r\]
trouvait son équilibre entre la force d’attraction électrostatique : \[\frac{m~v^2}{r}\]
due à la charge positive du noyau : \[q=Z~e\]
et la force d’inertie : \[f=\frac{m~v^2}{r}\]
On en déduit l’expression du rayon \(r\) de la trajectoire.
L’énergie totale de l’électron de la couche d’ordre \(n\) (somme de l’énergie cinétique et de l’énergie potentielle) est alors donnée par la relation : \[E_n=\frac{2~\pi^2~m~Z^2~e^4}{n^2~h^2}\]
On notera que, dans ce modèle, un seul nombre (\(n = 1,~2,~3\dots\)) caractérisait l’électron dans l’atome.
L’amélioration des techniques de détection et d’enregistrement des raies émises par l’atome permit de montrer que certaines raies que l’on avait classées comme simples avaient en fait une structure multiple.
Pour rendre compte de ce fait, les théoriciens devaient modifier l’image, la compléter, ne plus négliger les orbites elliptiques et le mouvement du noyau par rapport au centre de gravité de l’atome.
Sommerfeld entreprit cette tâche en 1916.
Il introduisit la quantification des trajectoires elliptiques ainsi que les concepts de la mécanique relativiste pour traiter le mouvement de l’électron sur ces nouvelles orbites.
Dans l’expression de l’énergie de l’électron intervient cette fois un deuxième nombre quantiques \(l\) pouvant prendre toutes les valeurs entières \(l\in[0~,~n-1]\). D’où une nouvelle expression de l’énergie, à priori plus complète : \[E_{n,~l}=E_n~\Big\{1+\frac{\alpha^2~Z^2}{n^2}~\Big(\frac{n}{l+1}-\frac{3}{4}\Big)\Big\}\]
-
\(E_n\) : énergie de Bohr (précédente)
-
\(\alpha\) : constante de structure fine
La couche \(K\) est simple, la couche \(L\) est à 2 niveaux, la couche \(M\) à 3 niveaux, etc.
La théorie se rapprochait de l’expérience mais on ne tarda pas à découvrir que le niveau \(L\) avait une structure fine de 3 raies au lieu de 2 et que le niveau \(M\) en avait 5 au lieu de 3.
Pour élargir sa théorie a priori complète Sommerfeld devait introduire un nombre quantique supplémentaire \(j\) appelé nombre quantique interne dont la signification physique ne paraissait pas très claire à l’époque.
L’action d’un champ magnétique sur les raies spectrales émises par les atomes devait donner le coup de grâce à l’image de l’atome.
Le dédoublement des raies sous l’action d’un champ magnétique, avait été effectivement observé par Zeeman. Cet effet Zeeman fait intervenir deux autres des grandeurs :
-
un moment cinétique dit moment angulaire orbital ;
-
un moment magnétique.
2. Moment cinétique
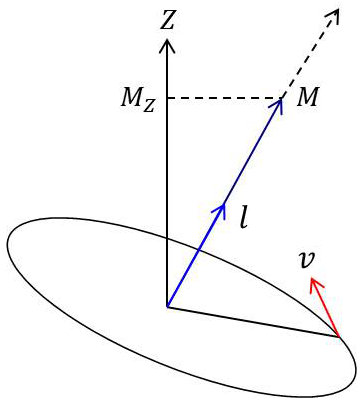 Par définition, le moment cinétique est le moment \(\overrightarrow{M_c}\) de la quantité de mouvement \(\overrightarrow{p}=m~\overrightarrow{v}\) de l’électron par rapport au noyau.
Par définition, le moment cinétique est le moment \(\overrightarrow{M_c}\) de la quantité de mouvement \(\overrightarrow{p}=m~\overrightarrow{v}\) de l’électron par rapport au noyau.
En mécanique ondulatoire, ce moment est quantifié : au vecteur \(\overrightarrow{M_c}\), on fait correspondre un vecteur \(\overrightarrow{l}\) ayant dans l’espace (\(2~l+1\)) des orientations discontinues. Ces deux vecteurs sont liés par la relation : \[\overrightarrow{M_c}=\frac{h}{2~\pi}~\overrightarrow{l}=\hbar~\overrightarrow{l}\]
On remarque que le nombre quantique \(l\) est proportionnel au moment orbital \(\overrightarrow{M_c}\).
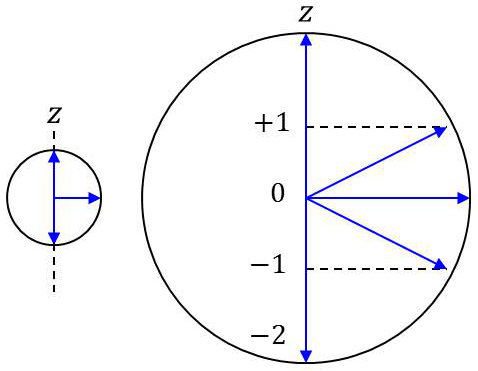 Les orientations de \(\overrightarrow{l}\) sont définies par rapport à un axe fixe sans signification physique particulière. On le désigne par axe de quantification \(OZ\).
Les orientations de \(\overrightarrow{l}\) sont définies par rapport à un axe fixe sans signification physique particulière. On le désigne par axe de quantification \(OZ\).
La projection \(\overrightarrow{M_z}\) du moment \(\overrightarrow{M_c}\) sur cet axe est également quantifiée. Ainsi, à l’état \([l=1]\) de l’électron correspondent 3 orientations possibles du moment cinétique \(\overrightarrow{M_c}\) et 5 orientations pour \([l=2]\).
On notera cependant, que ces états sont caractérisés par une même énergie \(E_{n,~l}\) qui ne dépend donc que des nombres quantiques \(n\) et \(l\). Ce point est important : si l’atome est situé dans un champ magnétique, les 3 états (\(l=1\)) et les 5 états (\(l=2\)) possèderont alors des énergies différentes, ce qui conduit à une séparation des niveaux (effet Zeeman).
3. Le moment magnétique
La gravitation des électrons autour du noyau est équivalente à l’ensemble des courants électriques qui transforment l’atome en un petit aimant. Celui-ci peut être caractérisé par son moment magnétique \(\overrightarrow{M_m}\).
En mécanique classique, on associe au moment cinétique \(\overrightarrow{M_c}\) un moment magnétique \(\overrightarrow{M_m}\) proportionnel au premier. Pour fixer les idées, raisonnons sur un exemple, simple celui de la trajectoire circulaire d’une charge élémentaire \(+e\) :
\[\begin{aligned} \overrightarrow{M_c}&=\overrightarrow{r}\wedge\overrightarrow{p}=\overrightarrow{r}\wedge m~\overrightarrow{v}=m~r^2~\overrightarrow{\omega}\\ \overrightarrow{M_m}&=\overrightarrow{S}~i\quad;\quad S=\pi~r^2\quad;\quad i=e~v=\frac{e~\omega}{2~\pi}\\ \overrightarrow{M_m}&=\frac{e}{2}~r^2~\overrightarrow{\omega}=\frac{e}{2~m}~\overrightarrow{M_c}\end{aligned}\]
En projection sur l’axe de quantification, on aura : \[\overrightarrow{M_{m,z}}=\frac{e}{2~m}~\overrightarrow{M_z}\]
4. Notion de spin
Placé dans un champ magnétique externe, l’électron acquiert un supplément d’énergie : \[\Delta E=M_{m,~z}~H\]
L’action du champ magnétique sur les raies spectrales apparaissait comme un phénomène compliqué, l’interprétation des résultats expérimentaux s’avérant difficile. La théorie s’avérait insuffisante pour expliquer un effet Zeeman anormal, les structures fines des spectres étant plus riches que ne le laissait prévoir la théorie.
Trois paramètres permettaient jusqu’à présent de définir l’électron dans l’atome, à savoir les trois nombres : \(n\), \(l\) et \(j\). Description toujours insuffisante. En 1925, on en revint à l’image classique de l’électron caractérisé par sa masse \(m\) et sa charge \(-e\), mais en l’assimilant toutefois à une sphère de charge négative uniformément distribuée.
Pour expliquer l’effet Zeeman anormal, cette description fut complétée par l’introduction d’un paramètre supplémentaire, en imaginant que l’électron tournait également sur lui-même à l’image d’une toupie. Ainsi est apparu un moment angulaire de rotation que l’on nomma spin. Comme le moment angulaire orbital, le spin fut quantifié : \[\overrightarrow{M_{rot}}=\frac{h}{2~\pi}~\overrightarrow{s}\]
La valeur de \(s\) fut alors choisie en accord avec l’expérience : \[s=\frac{1}{2}\qquad\text{en unités}\qquad\frac{h}{2~\pi}\]
Cette rotation de la charge élémentaire entraînait l’existence d’un moment magnétique intrinsèque : \[\overrightarrow{\mu}=\frac{h}{2~\pi}~\overrightarrow{M_{rot}}\]
En projection sur l’axe \(OZ\) : \[\overrightarrow{\mu_z}=\frac{h}{2~\pi}~\overrightarrow{M_{rot,~z}}\]
L’électron devenait assimilable à un petit aimant de forme sphérique en rotation autour du diamètre défini par la ligne des pôles.
En électromagnétisme classique, le rapport du moment magnétique au moment cinétique a pour valeur \(e/2~m\). Pour rendre compte de l’effet Zeeman anormal, on attribua au moment magnétique de l’électron une valeur double : \[\mu=\frac{e}{2~m}~\frac{h}{2~\pi}\]
L’expérience et, plus tard, la théorie de Dirac justifièrent cette valeur.
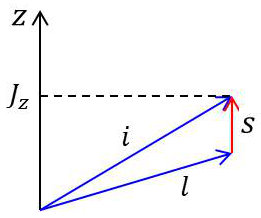 Cette grandeur pouvait s’interpréter comme la résultante des moments cinétiques (\(\overrightarrow{l},~\overrightarrow{s},~\overrightarrow{j}\)) représentant le moment angulaire total.
Cette grandeur pouvait s’interpréter comme la résultante des moments cinétiques (\(\overrightarrow{l},~\overrightarrow{s},~\overrightarrow{j}\)) représentant le moment angulaire total.
L’introduction du spin permettait maintenant de rendre compte de l’effet Zeeman dit anormal.
Pour autant, l’image de l’atome n’était toujours pas correcte. Pour élaborer une image du cortège électronique rendant compte de l’expérience, il fallait introduire encore un certain nombre de règles.
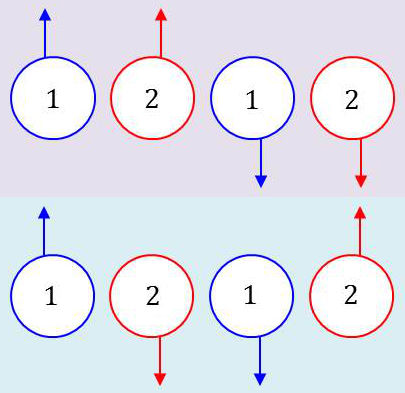 Envisageons par exemple un système de deux électrons [1] et [2]. Ceux-ci peuvent se placer suivant 4 configurations :
Envisageons par exemple un système de deux électrons [1] et [2]. Ceux-ci peuvent se placer suivant 4 configurations :
-
deux où les spins sont parallèles ;
-
deux où les spins sont antiparallèles.
Chaque électron possède un moment magnétique \(\mu\). Lorsque les spins sont parallèles (\(a\)), les moments magnétiques additionnent leurs effets. Lorsque les spins sont anti-parallèles (\(b\)), le moment magnétique résultant est nul.
Un tel système existe. Il s’agit de l’atome d’hélium \(He\) qui possède 2 électrons sur la couche \(K~(n = 1)\).
L’absence de propriétés magnétiques envisagées ci-dessus indique que les deux électrons ont leurs spins antiparallèles. Il semble interdit dans une configuration stable que les deux électrons de la couche \(K\) aient des spins identiques.
On peut généraliser, un électron étant caractérisé par 4 nombres quantiques \(n,~l,~j,~j_z\), projection de \(j\) sur l’axe de quantification. Le principe de Pauli postule alors qu’il est impossible que 2 électrons du cortège possèdent les mêmes valeurs des 4 nombres quantiques.
Ce principe d’exclusion limite un certain nombre de combinaisons possibles à priori. Il limite ainsi à 2 le nombre d’électrons gravitant sur la couche \(K\). Pour la couche \(L~(n = 2)\), nous aurons sur le niveau \(l = 0\), 2 électrons et sur le niveau \(l = 1\), au plus 6 électrons.
Le nuage électronique enveloppant le noyau était ainsi réduit à une construction géométrique nécessitant seulement 4 paramètres et certaines règles de combinaisons.

