1. Discussion sur les lois de Descartes
Nous avons évoqué les lois fondamentales de la réfraction et nous avons rappelé les lois de Snell-Descartes exprimant la relation entre le rayon incident et le rayon réfracté : \[n_1~\sin(i_1)~=~n_2~\sin(i_2)\]
Ou encore : \[\frac{\sin(i_1)}{\sin(i_2)}~=~\frac{n_2}{n_1}~=~n_{2/1}\]
Une discussion sur cette deuxième loi est nécessaire.
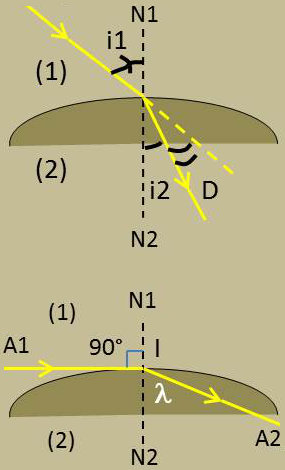 Considérons le cas où le milieu incident est moins réfringent (par exemple de l’air dans l’eau) : \[n_2~>~n_1 \qquad n_{2/1} > 1\]
Considérons le cas où le milieu incident est moins réfringent (par exemple de l’air dans l’eau) : \[n_2~>~n_1 \qquad n_{2/1} > 1\]
L’incidence peut varier de zéro (incidence normale) à 90° (incidence rasante). À chaque valeur de \(i_1\) et par suite de \(\sin(i_1)\) correspond une valeur acceptable de \(\sin(i_2)\) donc de \(i_2\).
Il y a donc toujours un rayon réfracté. La lumière passe toujours du milieu le moins réfringent dans le milieu le plus réfringent : \[\sin(i_2)~<~\sin(i_1)\]
Comme les angles sont compris entre 0° et 90°, il en résulte que \(i_2~<~i_1\).
De plus, ces deux angles sont de même signe, donc en pénétrant dans le milieu le plus réfringent, le rayon lumineux passe de l’autre côté de la normale et s’en rapproche.
1.1. Conditions aux limites
-
\(i_1~=0^o \quad\rightarrow\quad i_2~=~90^o\)
Pas de réfraction. Le rayon réfracté prolonge le rayon incident.
-
\(i_1~=~90^o \quad\rightarrow\quad i_2~=~\lambda\)
\(\lambda\) est appelé angle de réfraction limite :
\[\begin{aligned} &\frac{sin(\pi/2)}{\sin(\lambda)}~=~\frac{n_2}{n_1}\\ &\sin(\lambda)~=~\frac{n_1}{n_2}~=~n_{1/2}~=~\frac{1}{n_{2/1}}\end{aligned}\]
Tous les incidents qui frappent le dioptre en un même point \(I\) donnent des réfractés qui sont tous compris à l’intérieur d’un cône de révolution ayant pour sommet \(I\), pour axe la normale \(N_1IN_2\) au dioptre et pour demi-angle au sommet l’angle de réfraction limite.
Voici quelques valeurs de l’angle limite : \[\begin{matrix} &Milieu~1& &Milieu~2& &n_{2/1}& &Angle~limite\\ & & & & & & & \\ &Air& &Eau& &1,33& &48,5^o\\ &Air& &Crown& &1,52& &42,0^o\\ &Air& &Flint& &1,60& &38,5^o\\ &Air& &Diamant& &2,42& &24,5^o \end{matrix}\]
Pour comprendre le phénomène lorsqu’il s’agit du passage d’un milieu réfringent dans un milieu moins réfringent, on applique la réciprocité avec le principe du trajet inverse de la lumière. On en conclut d’ailleurs intuitivement que :
-
La lumière ne peut pénétrer du milieu le plus réfringent vers le milieu le moins réfringent que si l’angle d’incidence est au plus égal à un certain angle défini comme il a été dit et appelé angle de réflexion totale.
-
Quand il y a réfraction, le rayon lumineux en pénétrant dans le milieu moins réfringent passe de l’autre côté de la normale et s’en écarte.
2. Le dioptre plan
2.1. Définition. Recherche du stigmatisme.
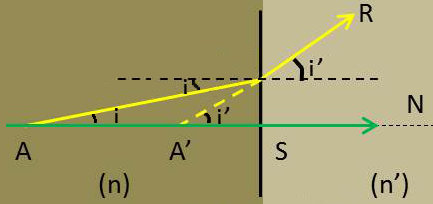 Un dioptre plan est l’ensemble de deux milieux transparents, homogènes et isotropes, inégalement réfringents, séparés par une surface plane. D’après la figure : \[n~\sin(i)~=~n'~\sin(i') \qquad (n'~>~n)\]
Un dioptre plan est l’ensemble de deux milieux transparents, homogènes et isotropes, inégalement réfringents, séparés par une surface plane. D’après la figure : \[n~\sin(i)~=~n'~\sin(i') \qquad (n'~>~n)\]
On choisit l’orientation gauche – droite.
Avec IS commun :
\[\begin{aligned} &\overline{SA}~\tan(i)~=~\overline{SA'}~\tan(i')\\ &\overline{SA'}~=~\overline{SA}~\frac{\tan(i)}{\tan(i')}\end{aligned}\]
Lorsque (i) varie, (i’) aussi ainsi que la position de A’ : il n’y a donc pas stigmatisme pour un point quelconque A placé hors de la surface dioptrique à distance finie.
2.1.1. Point objet sur la surface réfractante
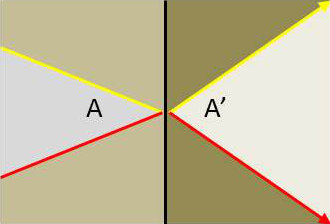 Si \(\overline{SA}=0\), alors \(\overline{SA'}=0\) : tout point de la surface réfractante est à lui-même son image.
Si \(\overline{SA}=0\), alors \(\overline{SA'}=0\) : tout point de la surface réfractante est à lui-même son image.
Ceci veut dire qu’un faisceau conique de rayons incidents venant converger en un point A de cette surface donne naissance à un faisceau conique divergent de rayons réfractés partant de A.
Le dioptre modifie simplement l’ouverture du faisceau.
2.1.2. Point objet à l’infini
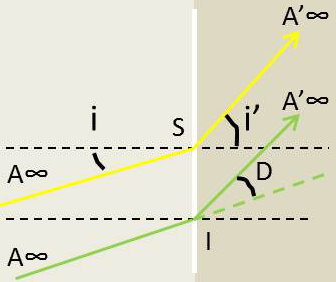 Quand le point objet est à l’infini, l’incidence (i) est invariable, il en est de même de (i’) et l’image A’ est également à l’infini. Il y a d’ailleurs stigmatisme rigoureux puisqu’un faisceau incident parallèle donne un faisceau émergent parallèle.
Quand le point objet est à l’infini, l’incidence (i) est invariable, il en est de même de (i’) et l’image A’ est également à l’infini. Il y a d’ailleurs stigmatisme rigoureux puisqu’un faisceau incident parallèle donne un faisceau émergent parallèle.
En résumé : quand le point objet est à l’infini, le dioptre plan est rigoureusement stigmatique :
-
Pour tout point de sa surface, le point image est alors confondu avec le point objet.
-
Pour tout point à l’infini dont l’image est aussi à l’infini, mais dans une direction généralement différente :
\[\widehat{A'IA}~=~D~=~i-i'\]
2.1.3. Autres cas
En dehors des cas particuliers précédents, le stigmatisme rigoureux est très difficile à obtenir. On peut parfois essayer d’obtenir un stigmatisme approché à partir de la relation :
\[\begin{aligned} &\overline{SA'}~=~\frac{n'}{n}~\frac{\cos(i')}{\cos(i)}~\overline{SA}\\ &\overline{SA'}~\simeq~\frac{n'}{n}~\overline{SA}\qquad \text{pour i et i' petits} \end{aligned}\]
Il y a donc stigmatisme approché pour tout point à distance finie qui n’envoie sur la surface qu’un pinceau de rayons faisant un petit angle avec la normale.
Il revient au même de dire que le dioptre plan est approximativement stigmatique pour tout point A d’une de ses normales Sx que nous pouvons prendre comme axe du dioptre à condition de limiter celui-ci au voisinage immédiat du pied S de cette normale.
Le dioptre doit travailler à faible ouverture.
2.2. Équation de conjugaison dans le cas du stigmatisme approché
Posons : \[\overline{SA}~=~x \quad;\quad \overline{SA'}~=~x'\]
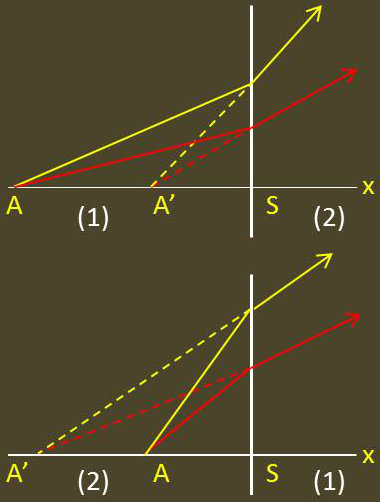 D’où : \[\frac{n'}{x'}~=~\frac{n}{x} \qquad \text{(x et x' toujours du même signe)}\]
D’où : \[\frac{n'}{x'}~=~\frac{n}{x} \qquad \text{(x et x' toujours du même signe)}\]
Point objet et point image sont d’un même côté de la surface optique.
Ils sont de natures différentes : à un point objet réel correspond une image virtuelle et inversement :
-
Si le milieu objet est le plus réfringent, le point image est plus près de la surface dioptrique que le point objet (schéma 1 ci-contre).
-
C’est le contraire lorsque le point objet est dans le milieu moins réfringent (schéma 2 ci-contre).
2.3. Image d’un objet
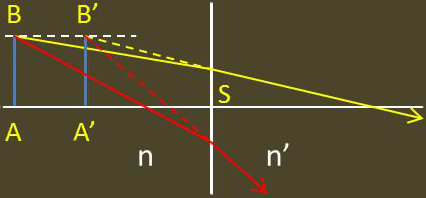 Plaçons-nous toujours dans les conditions de stigmatisme approché.
Plaçons-nous toujours dans les conditions de stigmatisme approché.
Le point A a pour image A’.
Soit B un point du plan mené par A perpendiculairement à AS.
Si B n’envoie, de même que A, qu’un pinceau de rayons tombant sous une faible incidence, il admet une image B’ située encore à la distance du dioptre, c’est-à-dire dans un plan A’B’ parallèle au dioptre.
Un dioptre plan de faible ouverture donne d’un petit objet perpendiculaire à son axe, centré sur lui (l’ouverture du dioptre et les dimensions de l’objet étant telles que les rayons des divers points de l’objet envoient sur la surface dioptrique la frappent sous une incidence faible), une image perpendiculaire à l’axe et centrée sur lui.
L’image a la même orientation que l’objet et les dimensions correspondantes sont égales.
3. Lame à faces parallèles
Une lame à faces parallèles est un milieu transparent homogène, limité par deux faces planes parallèles. Nous supposerons que les deux faces de la lame sont baignées par le même milieu.
La lame est alors complètement caractérisée par son épaisseur e et son indice relatif n par rapport au milieu extérieur.
Nous nous bornerons au cas où la substance est plus réfringente que l’extérieur (\(n~>~1\)) ; par exemple lame de verre dans l’air ou dans l’eau.
3.1. Action de la lame sur un rayon lumineux
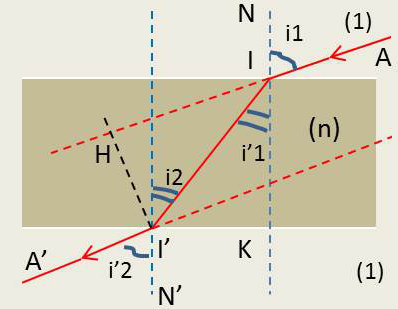 La lame à faces parallèles ne dévie pas les rayons lumineux qui la traversent. Ces rayons sont déplacés latéralement.
La lame à faces parallèles ne dévie pas les rayons lumineux qui la traversent. Ces rayons sont déplacés latéralement.
L’explication est intuitive en raison de la géométrie du système et par application du principe de retour inverse de la lumière (les milieux extrêmes étant identiques).
Calculons la translation subie par un rayon incident donné. Cette translation est I’H. Dans le triangle rectangle IHI’, nous avons : \[I'H~=~II'\sin(i_1-i_2)\]
Mais dans le triangle IKI’ : \[II'=\frac{e}{\cos(i_2)}\]
Il vient alors : \[I'H=e~\frac{\sin(i_1-i_2)}{\cos(i_2)}\]
La translation subie par le rayon est proportionnelle à l’épaisseur de la lame lorsque l’indice de la lame et l’incidence sous laquelle elle travaille restent constants.
Pour une même lame, elle croît avec l’incidence et varie de 0 à e lorsque l’incidence augmente de 0° à 90°. Un rayon normal aux faces traverse la lame en ligne droite ; un rayon qui entre en rasant la face d’entrée sort en rasant la face de sortie.
3.2. Recherche du stigmatisme
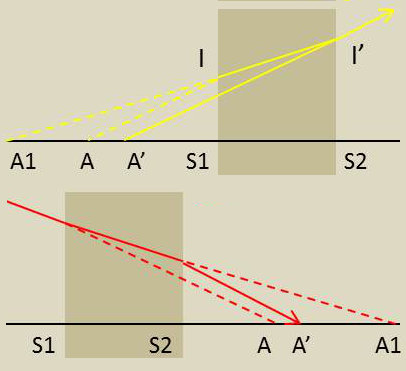 La lame est un système optique formé par l’association de deux dioptres plans parallèles qui sont ses deux faces. Elle sera stigmatique pour un point si le stigmatisme est réalisé successivement pour les deux dioptres. Donc :
La lame est un système optique formé par l’association de deux dioptres plans parallèles qui sont ses deux faces. Elle sera stigmatique pour un point si le stigmatisme est réalisé successivement pour les deux dioptres. Donc :
Il y aura stigmatisme rigoureux pour tout point à l’infini, dont la lame donne une image à l’infini dans la même direction.
Il ne peut y avoir stigmatisme approché pour un point placé à distance finie, que s’il n’émet qu’un pinceau formé de rayons sensiblement normaux aux faces de la lame.
Dans ces conditions, la face d’entrée donne du point \(A\) une image \(A_1\) située sur la normale \(AS_1S_2\) et dont la position est définie par la relation : \[\overline{S_1A_1}~=~n~\overline{S_1A}\]
Supposons \(A\) réel, \(A_1\) est alors virtuel. Ce point joue le rôle d’objet réel par rapport au dioptre formé par la face de sortie de la lame et envoie sur lui un pinceau de rayons dont l’incidence est faible.
Ce dioptre travaille donc dans des conditions de stigmatisme approché et donne de \(A_1\) une image \(A'\) située sur \(A_1S_1S_2\) : \[\overline{S_2A'}~=~ \frac{1}{n}~\overline{S_2A_1}\]
\(A'\) est l’image de \(A\) donnée par la lame à faces parallèles. Elle est ici virtuelle.
Étudions à présent le cas inverse. Évaluons la distance de l’image à l’objet. Nous avons : \[\overline{AA'}~=~\overline{AS_1}~+~\overline{S_1S_2}~+~\overline{S_2A'}~=~-x_1~+~e~+~x'_2\]
Or : \[x'_2~=~\frac{x_2}{n}~=~\frac{x'_1-e}{n}~=~x_1-\frac{e}{n}\]
D’où l’on tire : \[AA'~=~e~\frac{n-1}{n}\]
Cette distance ne dépend pas de la position du point \(A\) par rapport à la lame. Elle ne dépend que de l’épaisseur e de la lame et de son indice n.
3.3. Image d’un objet
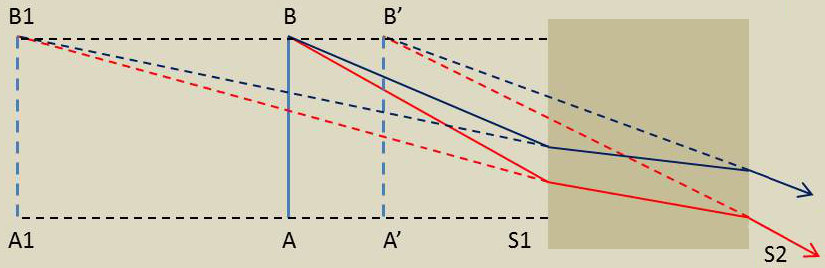 Raisonnons comme dans le cas du dioptre plan.
Raisonnons comme dans le cas du dioptre plan.
On voit que la lame donne d’un petit objet plan perpendiculaire à l’axe de la lame une image plane perpendiculaire à l’axe et centrée sur lui, à condition toutefois que l’on n’utilise que des rayons faiblement inclinés sur l’axe.
Cette image est égale à l’objet et elle a la même orientation que lui.
Sa distance à l’objet est égale à :\(\quad e~\cfrac{n-1}{n} \)
4. Prisme
Un prisme est un milieu transparent (supposé ici homogène et isotrope) limité par deux dioptres plans non parallèles AP et AP’ que l’on appelle les faces du prisme. Les deux faces se coupent suivant une droite AA’ qui est l’arête du prisme. L’angle plan du dièdre qu’elles forment est l’angle du prisme.
Toute section du prisme, telle que PAP’, faite perpendiculairement à l’arête, s’appelle section principale. Un prisme est complètement déterminé par son angle A et par son indice relatif n par rapport au milieu extérieur (il résulte de nos hypothèses que \(n~>~1\)).
4.1. Marche d’un rayon lumineux dans une section principale
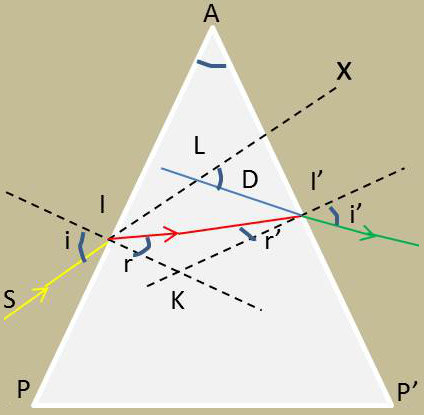 Soit SI un rayon incident contenu dans un plan de section principale, qui est aussi plan d’incidence et que nous prenons pour plan de la figure. Ce rayon arrive sur la première face du prisme sous l’angle d’incidence \(i\).
Soit SI un rayon incident contenu dans un plan de section principale, qui est aussi plan d’incidence et que nous prenons pour plan de la figure. Ce rayon arrive sur la première face du prisme sous l’angle d’incidence \(i\).
Puisque \(n>1\), le rayon pénètre dans le prisme. Il reste dans le plan de section principale et se rapproche de la normale suivant II’, en faisant un angle de réfraction \(r\).
Il arrive sur la deuxième face sous un angle d’incidence que nous désignerons par \(r'\).
Deux cas peuvent alors se produire suivant la valeur des angles comparés à l’angle limite \(\lambda\) :
-
\(r'~>~\lambda\) : Le rayon II’ se réfléchit totalement sur la face de sortie.
Il n’y a pas de rayon émergent. -
\(r'~<~\lambda\) : Le rayon sort suivant I’S’ en restant dans le plan de section principale.
Il s’écarte de la normale N’I’ et fait un angle d’émergence \(i'\).
Le rayon émergent n’est pas dans le prolongement du rayon incident et ne lui est pas parallèle. Le prisme a dévié le rayon lumineux et l’a dévié vers la base d’un angle désigné par D : \[D=(i-r)-(i'-r')\]
Nous partons des relations :
\[\begin{aligned} \sin(i)~&=~n~\sin(r)\\ \sin(i')~&=~n~\sin(r')\\ A~&=~r+r'\end{aligned}\]
La dernière provenant du quadrilatère inscriptible AIKI’ (deux angles droits) dans lequel on voit que l’angle A ainsi que la somme des angles (r + r’) sont supplémentaires de l’angle K. On obtient ainsi quatre relations fondamentales :
\[\begin{aligned} \sin(i)~&=~n.\sin(r)\\ \sin(i')~&=~n.\sin(r')\\ A~&=~r+r'\\ D~&=~i+i'-A\end{aligned}\]
4.2. Conditions d’émergence
 Tout rayon incident pénètre dans le prisme mais ne sort pas nécessairement.
Tout rayon incident pénètre dans le prisme mais ne sort pas nécessairement.
Cherchons d’abord à quelle condition doit satisfaire l’angle \(A\) du prisme pour que parmi tous les rayons incidents qui viennent frapper la face d’entrée en un même point I et qui sont contenus dans le plan de section principale passant par ce point, il y en ait qui émergent.
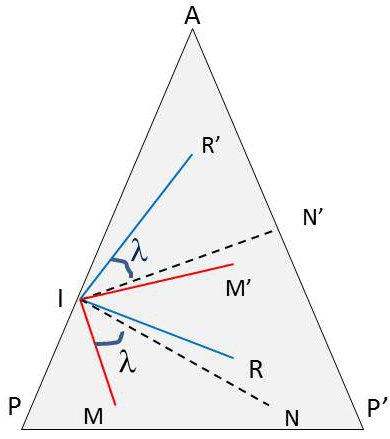
Tout rayon réfracté faisant avec la normale IN un angle au plus égal à l’angle limite \(\lambda\) est inférieur à l’angle [MIM’] = 2\(\lambda\) dont la bissectrice est la normale à la face d’entrée.
Il sort s’il fait avec la normale à la face de sortie un angle au plus égal à \(\lambda\) , donc s’il est contenu dans l’angle [RIR’] = 2\(\lambda\) dont la bissectrice est IN’, normale à la face de sortie.
La condition pour qu’il y ait des rayons sortants est donc que les deux angles [MIM’] et [RIR’] aient une partie commune. Il en sera ainsi si l’angle [NIN’] des deux bissectrices est au plus égal à \(2\lambda\). Tous les réfractés appartenant à cette région commune émergeront.
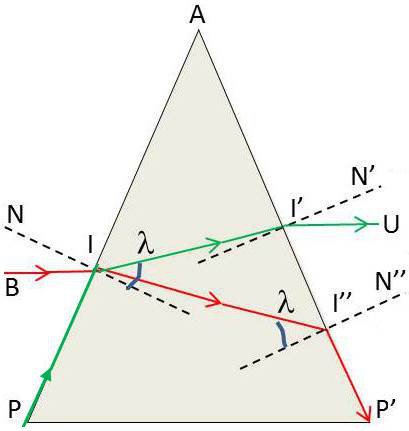 Mais [NIN’] = A (angles à côtés perpendiculaires), d’où la condition cherchée : \[A~\leq~ 2\lambda\]
Mais [NIN’] = A (angles à côtés perpendiculaires), d’où la condition cherchée : \[A~\leq~ 2\lambda\]
Si \(A<2\lambda\), certains rayons sont capables d’émerger. Ce sont ceux qui correspondent à des rayons réfractés situés dans la partie commune aux angles [MIM’] et [RIR’], c’est-à-dire dans l’angle [RIR’].
Celui qui se trouve dans les conditions les plus défavorables est celui qui, après réfraction à travers la face d’entrée, tombe sur la face de sortie sous l’incidence la plus faible possible.
Or, à la plus petite valeur de l’angle \(r'\) correspond la plus grande valeur possible pour l’angle \(r\) (puisque \(r+r'~=~A\)), soit \(\lambda\), ce qui entraîne \(i~=~90^o\).
Ce rayon est donc l’incident \(PI\) qui rase la face d’entrée en venant de la base ; il se réfracte en \(I'U\) faisant un angle d’émergence \(i'_1\) tel que : \[\sin(i'_1)~=~n~\sin(r'_1)~=~n~\sin(A-r_1)~=~n~\sin(A-\lambda)\]
Faisons tourner le rayon incident dans le plan de section principale autour de I de manière à le rapprocher de la normale. L’angle \(i\) décroît, il en est de même pour l’angle \(r\). Par suite l’angle \(r'\) augmente tandis que le point I’ se déplace sur AP’ en s’éloignant de l’arête du prisme.
À un moment donné l’angle \(r'\) est devenu égal à \(\lambda\), le rayon émergent I"P’ rase la face de sortie se dirigeant vers la base du prisme. Le rayon incident occupe alors une position limite BI. BI est le dernier rayon qui, frappant en I la face d’entrée, sort du prisme. L’angle d’incidence \(i_2\) qui lui correspond est donné par la relation : \[\sin(i_2)~=~n~\sin(r_2)~=~n~\sin(A-r'_2)~=~n~\sin(A-\lambda)\]
On a donc \(i_2=i'_1\) comme on peut le voir immédiatement en appliquant le principe du retour inverse au rayon PII’U.
Tous les rayons qui traversent le prisme sont donc ceux dont l’incidence est comprise entre 90° et une valeur \(i_2\) définie par la relation : \[\sin(i_2)~=~n~\sin(A-\lambda\]
Ceux qui rencontrent en I la face d’entrée sont contenus dans l’angle [BIP].
4.3. Étude de la déviation D
Lorsqu’un rayon lumineux monochromatique tombe sous l’incidence \(i\) sur la face d’entrée d’un prisme donné (A, n), il subit une déviation D. Nous allons chercher quelle est l’influence sur la déviation D de chacune des trois variables indépendantes A, n et i.
4.3.1. Influence de A (i et n constants)
L’expérience montre que la déviation augmente quand l’angle du prisme croît. Mais deux démonstrations permettent de l’appuyer :
-
Puisque \(i\) et \(n\) sont constants, \(r\) est constant, donc si A croît, et par suite, (\(i'-r\)) augmente. La relation \(D=(i-r)+(i'-r')\) nous montre qu’alors D augmente.
-
On peut, à partir des formules, calculer et constater que cette dérivée est positive ; on trouve en effet :
\[\frac{dD}{dA}=\frac{n~\cos(r')}{\cos(i')}-1\]
4.3.2. Influence de n (i et A constants)
L’expérience montre que la déviation augmente lorsque l’indice du prisme croît. La théorie permet d’appuyer l’expérience. On part du groupe des relations fondamentales :
\[\begin{aligned} \sin(i)~&=~n~\sin(r)\\ \sin(i')~&=~n~\sin(r')\\ A~&=~r+r'\\ D~&=~i+i'-A\end{aligned}\]
-
Les relations montrent que, \(i\) étant constant, \(r\) diminue si \(n\) augmente. Puisque A est constant, il s’ensuit un accroissement de \(r'\) qui entraîne un accroissement de \(i'\) dû d’une part à l’augmentation de \(n\), d’autre part à l’accroissement de \(r'\). D va donc en croissant.
-
Si on forme l’expression de \(dD/dn\), on trouve qu’elle est toujours positive : on peut en effet différentier les relations sous la forme :
\[\begin{aligned} 0&=n~\cos(r)~dr+\sin(r)~dn\\ \cos(i')~di'&=n.\cos(r')~dr'+\sin(r')~dn\\ 0&=dr+dr'\\ dD&=di'\end{aligned}\]
En éliminant les variables intermédiaires : \[\frac{dD}{dn}=\frac{\sin(A)}{\cos(r)~\cos(i')}\]
4.3.3. Influence de i (A et n constants)
En utilisant un goniomètre on peut faire des expériences quantitatives et déterminer pour chaque valeur de \(i\) la valeur correspondante de D.
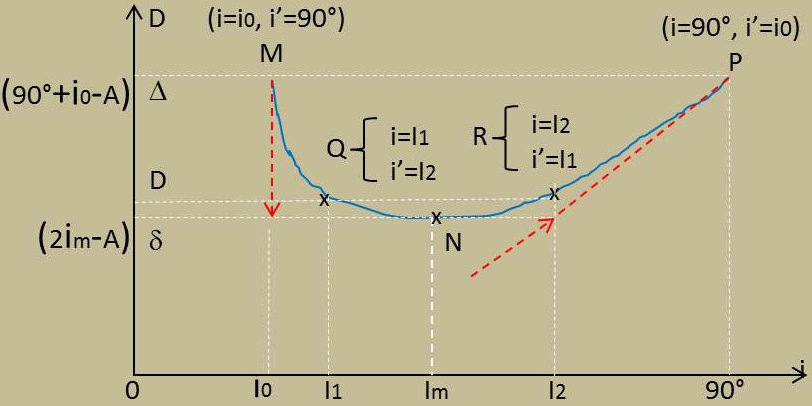 Il est alors possible de construire point par point la courbe représentative C (pour un prisme donné et une radiation déterminée) des valeurs de D en fonction de \(i\). Son allure est indiquée ci-contre.
Il est alors possible de construire point par point la courbe représentative C (pour un prisme donné et une radiation déterminée) des valeurs de D en fonction de \(i\). Son allure est indiquée ci-contre.
-
Elle est comprise entre les points extrêmes M et P.
-
M correspond à la valeur limite \(i_0\) de l’incidence (l’émergence est alors +90°).
-
P correspond à l’incidence +90°, l’émergence étant alors \(i_0\).
-
Aux points M et P la déviation est \(\Delta\) , la plus grande possible.
-
En N elle est la plus petite possible \(\delta\) (minimum de déviation).
Remarques
On remarquera la réciprocité incidence – émergence entre deux points tels que Q et R.
Si D prend la valeur \(\delta\), les points Q et R viennent se confondre en N, leurs abscisses deviennent égales à \(i_m\). Au minimum de déviation, les angles d’incidence et d’émergence sont donc égaux : \[i~=~i'~=~i_m\]
La courbe suppose \(i_0~>~0\), l’angle du prisme est compris entre \(\lambda\) et \(2\lambda\). Si l’on avait \(A~=~\lambda\), le point M serait sur l’axe OD. Si l’on avait \(A~<~\lambda\), le point M serait à gauche de OD, son abscisse \(i_0\) serait alors négative.
La tangente à la courbe en M est verticale. La tangente en P est parallèle à la première bissectrice si l’échelle des ordonnées est la même que celle des abscisses.
4.3.4. Démonstration théorique de l’existence du minimum de déviation
On évalue \(dD/di\) en différentiant les relations fondamentales. Tous calculs faits on obtient :
\[dD~=~\left\{1-\frac{\cos(i)}{\cos(i')}~\frac{\cos(r')}{\cos(r)}\right\}~di\]
1) Cette expression s’annule si : \[\cos(i)~\cos(r')~=~\cos(i')~\cos(r)\]
Élevons au carré, introduisons les sinus et éliminons les angles r et r’ en tenant compte des relations fondamentales. Toutes simplifications faites, il vient :
\[\begin{aligned} &\left(1-\frac{1}{n^2}\right)~\big[\sin^2(i)-\sin^2(i')\big]=0\\ &n\neq 1\qquad \text{donc}\qquad i~=~\pm i'\end{aligned}\]
2) Seule la solution (\(i=i'\)) convient. La solution (\(i=-i'\)) entraînerait (\(r=-r'\)), ce qui ne peut avoir lieu car \((r+r'=A)\neq 0\).
C’est en élevant au carré les deux membres d’une relation précédente que cette solution étrangère au problème physique a été introduite.
La dérivée de D s’annule pour : \[i~=~i'\qquad \Rightarrow \qquad r~=~r'\]
3) La condition (\(i=-i'\)) ne peut être réalisée qu’une seule fois au cours des variations de i. En effet i et i’ varient respectivement dans le même sens que r et r’. Mais r et r’ varient toujours en sens inverse, leur somme A étant une constante ; ils n’auront qu’une seule fois des valeurs égales. La dérivée ne s’annule donc qu’une seule fois au cours des variations de i. La déviation D présente donc, soit un seul maximum, soit un seul minimum au cours de ces variations.
4) Il reste à voir s’il s’agit d’un maximum ou d’un minimum. Nous pourrions former la dérivée seconde de D, son signe nous renseignant sur la concavité de la courbe. Mais il est plus simple de procéder comme suit : cherchons la valeur de \(dD/di\) pour i = 90° ; nous obtenons la valeur 1.
Cette dérivée est positive ; donc au voisinage de l’incidence rasante, D et i varient dans le même sens ; si i décroît à partir de 90°, D commence par décroître et par suite passera par un minimum. En résumé, lorsque (\(i=i'=i_m\)), la déviation D est la plus petite possible : \[\delta~=~2~i_m-A\]
4.4. Application du minimum de déviation
La méthode du minimum de déviation permet de mesurer les indices de réfraction. Au minimum de déviation nous avons : \[\delta~=~2~i_m-A\qquad \Rightarrow \qquad i_m=\frac{A+\delta}{2}\]
D’autre part : \[r_m~=~r'_m~=~\frac{A}{2}\]
On a donc : \[\sin\frac{A+\delta}{2}=n~\sin\frac{A}{2}\quad\Rightarrow\qquad n=\frac{\sin\cfrac{A+\delta}{2}}{\sin\cfrac{A}{2}}\]
De la mesure de l’angle A du prisme et de celle de la déviation minimum \(\delta\) qu’il impose à un rayon monochromatique, on peut déduire l’indice n du prisme par rapport à l’air pour la radiation considérée. Cette méthode employée pour les solides permet la détermination de n avec 5 décimales exactes.
Cas particulier d’un prisme de petit angle
Les angles étant petits, on peut faire les approximations : \[i~=~n~r\quad;\quad i'~=~n~r'\]
L’expression : \[D~=~i+i'-A\]
peut alors s’écrire : \[D~=~(n-1)~A\]
Pour de petits angles, cette déviation qui est faible ne dépend donc pas de l’incidence et elle est proportionnelle à l’angle A du prisme.

