1. Pupilles composées
C’est un ensemble de pupilles individuelles. Nous supposons qu’elles sont toutes percées dans le même écran. En un point du plan d’observation l’amplitude diffractée est la somme des amplitudes diffractées par chacune des pupilles.
Considérons l’une des pupilles et l’amplitude qu’elle diffracte : \[A_{\Sigma}=A_0\iint\limits_{\Sigma}t(x,y)~\exp\big\{j~2\pi~\big(\frac{\alpha'-\alpha}{\lambda}~x+\frac{\beta'-\beta}{\lambda}~y\big)\big\}~dx~dy\]
Imposons-leur une translation \(\quad \overrightarrow{T}(X,Y)~~;~~\Sigma\rightarrow\Sigma' \).
Posons : \(\quad x'=x-X\quad;\quad y'=y-Y \).
On a alors : \[A_{\Sigma'}=A_0\iint\limits_{\Sigma'}t(x',y')~\exp\big\{j~2\pi~\big([~]~x'+[~]~y'\big)\big\}~\exp\big\{j~2\pi~\big([~]~X+[~]~Y\big)\big\}~dx'~dy'\]
Cette intégrale sur \(\Sigma'\) est identique à la précédente sur \(\Sigma\), au déphasage près : \[A_{\Sigma'}=A_{\Sigma}~\exp(j~\varphi)\qquad\text{avec :}\quad\varphi=(\overrightarrow{k'}-\overrightarrow{k})\cdot\overrightarrow{T}\]
1.1. Ensemble de pupilles identiques
On considère un ensemble de pupilles disposées au hasard. Soit \(A_0\) l’amplitude diffractée par l’une d’entre elles et soient les translations \(\overrightarrow{B_i}\) permettant de passer aux autres pupilles (au total \(n\) pupilles). Le terme de phase sera : \[\exp(-j\varphi)=\exp\{j~(\vec{k'}-\vec{k})\cdot\overrightarrow{B_i}\}\]
Les \(n\) pupilles diffractent respectivement (depuis la pupille \(0\)) : \[A_0~;~A_0\exp(-j\varphi_1)~;~A_0\exp(-j\varphi_2)~;~\dots~;~A_0\exp(-j\varphi_{n-1})\]
L’amplitude totale diffractée sera : \[A=A_0~\{1+\exp(-j\varphi_1)+\exp(-j\varphi_2)+\exp(-j\varphi_3)+\dots+\exp(-j\varphi_{n-1})\}\]
Et pour l’intensité diffractée correspondante : \[AA^*=A_0A_0^*~\{1+\exp(-j\varphi_1)+\exp(-j\varphi_2)+\dots\}~\{1+\exp(j\varphi_1)+\exp(j\varphi_2)+\dots\}\]
Soit, sous une autre forme :
\[\begin{aligned} &AA^*=A_0A_0^*~\Big\{n+\sum_{i,j}\exp\big[j(\varphi_i-\varphi_j)\big]+\exp\big[j(\varphi_j-\varphi_i)\big]\Big\}\\ &AA^*=A_0A_0^*~\Big\{n+2\sum_{i,j}\cos(\varphi_i-\varphi_j)\Big\}\end{aligned}\]
\(n\) étant supposé très grand, \(\Delta\varphi_{i,j}=\varphi_i-\varphi_j\) peut prendre toutes les valeurs possibles de sorte que, en moyenne, les cosinus s’annulent deux à deux, ce qui entraîne \(I = n~I_0\).
Mais cette formule n’est plus vraie quand on considère un nombre fini de pupilles. C’est le cas par exemple pour les fentes de Young ou pour deux pupilles circulaires.
1.2. Fentes de Young
On reprend une expérience déjà décrite, mais en tenant compte de la largeur \(a\) des fentes \(S_1\) et \(S_2\) distantes de \(l\).
L’amplitude diffractée par une fente est : \[A_1=A_0~a~b~\operatorname{sinc}\big(\frac{\pi a\alpha'}{\lambda}\big)\]
On remarque que \(S_2\) se déduit de \(S_1\) par la translation \(\overrightarrow{T}=l~\overrightarrow{x}\).
D’où le déphasage : \[\varphi=(\overrightarrow{k}-\overrightarrow{k'})\cdot\vec{T}=-2\pi~\frac{\alpha'l}{\lambda}\]
Pour l’amplitude : \[A_2=A_1~\exp(-j\varphi)\]
Amplitude totale diffractée dans la direction \(\overrightarrow{k'}\) : \[A=A_1~\{1+\exp(-j\varphi)\}\quad;\quad A^*=A_1^*~\{1+\exp(+j\varphi)\}\]
D’où l’expression de l’intensité diffractée : \[I=AA^*=A_1A_1^*~(2+2\cos~\varphi)=4~A_1A_1^*~\cos^2(\varphi/2)\]
On écrira : \[I=I_0~\operatorname{sinc}^2\big(\frac{\pi a\alpha'}{\lambda}\big)\cdot~4\cos^2\big(\frac{\pi\alpha'l}{\lambda}\big)\quad;\quad I_0=A_0A_0^*~[ab]^2\]
On voit que l’on peut écrire : \[I(\alpha')=D(\alpha')~ J(\alpha')\]
\(D\) étant un terme de diffraction et \(J\) un terme d’interférences. On va observer des franges d’interférences, imprimées sur des franges de diffraction.
Comme \(l \gg a\), les franges d’interférences seront plus serrées que les franges de diffraction. Ainsi, entre deux grosses franges noires de diffraction apparaissent des franges très fines d’interférences.
1.3. Trous de Young
Dans le cas de trous de Young, on retrouvera un phénomène analogue à cette différence près que, sur de gros anneaux de diffraction s’imprimeront des franges très fines et moins sombres d’interférences.
2. Pupilles complémentaires
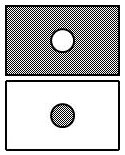Deux pupilles \(P\) et \(P'\) sont dites complémentaires quand la somme de leurs transmissions est égale à \(1\). Ces pupilles ne présentent qu’un intérêt théorique, car on ne sait pas les réaliser en pratique.
Considérons donc les deux pupilles éclairées par une source ponctuelle.
\(A\) est la vibration produite en un point \(M\) dans le plan de l’image géométrique de la source par la pupille. \(A'\) est la vibration produite au même point par la pupille \(P'\).
Si on suppose maintenant qu’on laisse passer à la fois la lumière traversant \(P\) et celle traversant \(P'\), on a en \(M\) la somme des deux vibrations \(A+A'\).
Or dans ce cas, on utilise la vibration tout entière et il n’y a pas de diffraction, c’est-à-dire qu’il n’y a pas de lumière en dehors de l’image géométrique \(S'\) de la source, image ponctuelle. Donc en dehors du point \(S'\), on a \(A + A' = 0\) ou \(A' = -A\).
Théorème de Babinet
Les figures de diffraction de Fraunhoffer de deux pupilles complémentaires sont identiques.
3. Pouvoir séparateur des instruments d’optique
La valeur d’un instrument dépend essentiellement de la possibilité qu’il offre de distinguer des détails très fins, c’est-à-dire d’apercevoir distinctes l’une de l’autre les images de deux points voisins \(A\) et \(A'\).
Cette séparation peut toujours être réalisée en prenant un oculaire assez grossissant ou une plaque photographique à grains assez fins, si les taches de diffraction fournies par l’objectif sont séparées par un intervalle obscur, ou tout au moins par une région moins éclairée.
Nous prendrons comme mesure du pouvoir séparateur de l’instrument celui de son objectif et nous admettrons que deux taches de diffraction apparaissent séparées à l’œil lorsque le maximum central coïncide avec le premier minimum nul de l’autre.
3.1. Lunette astronomique
L’objectif d’une lunette astronomique est une pupille circulaire de diamètre \(2R\).
On sait que le rayon angulaire du premier anneau noir est donné par : \[r=\alpha f=\frac{1,22~\lambda}{2R}~f\qquad\qquad f\text{ : distance focale}\]
Pour que deux étoiles \(A\) et \(A'\) puissent être séparées, leur distance angulaire doit être \(\alpha\).
Il y a cependant une difficulté dans le choix de \(\lambda\), car les étoiles envoient de la lumière blanche. Les anneaux sont colorés et il n’est guère possible de préciser la valeur qu’il faut choisir pour \(\lambda\). On choisit cependant la valeur \(\lambda=5,5\) Å qui correspond au maximum de sensibilité pour l’œil.
3.2. Microscope
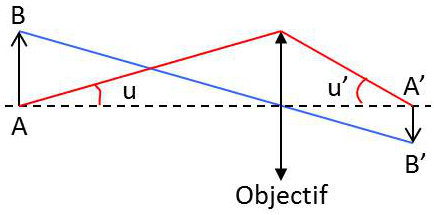Le rayon du premier anneau noir d’un microscope est : \[r=\frac{1,22~\lambda}{2R}~d\qquad\qquad d=OA'\]
L’objectif devant être stigmatique pour \(A\) et \(A'\), la relation d’Abbe doit être vérifiée : \[n~\sin(u)~AB=n'~\sin('u)~A'B'\quad\Rightarrow\quad AB=A'B'~\frac{n'~\sin(u')}{n~\sin(u)}\]
AB sera minimum si : \(\quad A'B'=\cfrac{1,22}{\lambda}~d \)
On a alors : \[AB=\frac{1,22}{2}~\frac{d}{R}~\frac{n'}{n}~\frac{\sin(u')}{\sin(u)}\]
Compte tenu de l’approximation (petits angles) \[\frac{R}{d}=\tan(u')\approx\sin(u')\quad\Rightarrow\quad\frac{d}{R}~\sin(u')\approx 1\]
Posons \(n_0=\dfrac{n}{n'}\), indice du milieu objet / milieu image.
Le pouvoir séparateur du microscope est donc : \[AB=\delta=\frac{1,22~\lambda}{2~n_0~\sin(u)}\]
\(n_0~\sin(u)\) est l’ouverture numérique de l’objectif.
3.3. Spectroscope à prisme
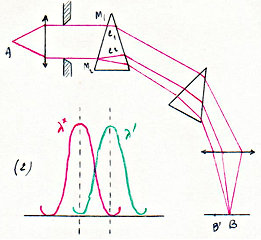Deux longueurs d’onde \(\lambda\) et \(\lambda'\) sont juste séparées si le maximum de \(\lambda\) coïncide avec le minimum de \(\lambda'\), les deux courbes se coupant à mi-hauteur du maximum.
Considérons alors le train de prismes :
\[\begin{aligned} &max_1(\lambda)~:&(AM_1B)_{\lambda}-(AM_2B)_{\lambda}&=0\\ &min_1(\lambda)~:&(AM_1B)_{\lambda'}-(AM_2B)_{\lambda'}&=\lambda'\end{aligned}\]
D’après le principe de Fermat : \[\delta(\Sigma n~e)=\Sigma n~e'-\Sigma n~e\]
C’est un infiniment petit du deuxième ordre par rapport aux distances des trajectoires.
Ainsi :
\[\begin{aligned} &(AM_1B)_{\lambda'}-(AM_1B)_{\lambda}=\Sigma e_1\Delta n\\ &(AM_2B)_{\lambda'}-(AM_2B)_{\lambda}=\Sigma e_2\Delta n\end{aligned}\]
Et compte tenu des relations, il vient : \[\Sigma e_1\Delta n-\Sigma e_2\Delta n=\lambda'\]
Pour un milieu donné, on peut faire l’approximation : \[\frac{\Delta n}{\Delta\lambda}\approx\frac{dn}{d\lambda}\quad\text{ou}\quad\Delta n\approx\frac{dn}{d\lambda}~\Delta\lambda\]
On peut alors écrire : \[\Delta n(\Sigma e_1-\Sigma e_2)=\lambda'\approx\lambda=\frac{dn}{d\lambda}~\Delta\lambda~(\Sigma e_1-\Sigma e_2)\]
Par suite : \[R=\frac{\lambda}{\Delta\lambda}=\Sigma(e_1-e_2)\Delta n\]
Remarque
Pour un prisme unique (arête \(e_1\approx 0\) et base \(e_2\approx e\)) : \[R=\frac{\lambda}{\Delta\lambda}=e~\frac{dn}{d\lambda}\]
4. Problème de l’apodisation
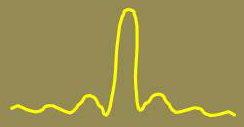Dans une figure de diffraction, il apparaît des lobes secondaires (franges ou pieds), porteurs d’une certaine fraction de l’intensité, fraction dont l’importance ne doit pas être systématiquement négligée, surtout si l’on est amené à étudier deux objets voisins de brillances différentes : l’image principale correspondant à l’intensité du plus faible peut se trouver noyée dans les franges lointaines de l’autre objet, le plus brillant.
On est ainsi amené à considérer des ouvertures à distribution d’amplitude \(f(x,y)\neq 1\) permettant de modifier l’intensité relative des pieds sans trop changer la largeur du corps de figure.
La suppression des pieds est ce que l’on appelle l’apodisation et l’écran produisant la répartition convenable d’amplitude lumineuse est dit écran apodisant. L’amplitude a alors une expression de la forme : \[A(\mu,\nu)=\iint\limits_{\Sigma}f(x,y)~\exp\{j(\mu x+\nu y)\}~dx~dy\]
On reconnaît la transformation de Fourier à deux dimensions entre \(A\) et \(f\).
L’intégration peut porter sur un domaine infini à condition de faire :
\[\begin{aligned} &f=f\quad\text{pour}\quad M\in\Sigma\\ &f=0\quad\text{pour}\quad M\notin\Sigma\end{aligned}\]
Peut-on fabriquer un écran pour avoir \(A\) désiré ? Autrement dit, \(A\) étant donné, peut-on avoir \(f\) ? Mathématiquement oui, mais physiquement, c’est difficilement réalisable et on doit imposer à \(A\) des conditions assez souples. Par exemple, une énergie maximale à l’intérieur d’un angle \(\theta\) donné.
