1. Rappel

On rappelle que, au passage à l’interface de deux milieux [1] et [2], il y a continuité des composantes :

– Tangentielles des champs : \[E_{1_T}=E_{2_T}\quad;\quad H_{1_T}=H_{2_T}\]

– Normales des inductions : \[D_{1_N}=D_{2_N}\quad;\quad B_{1_N}=B_{2_N}\]

2. Vecteur E parallèle au plan d’incidence

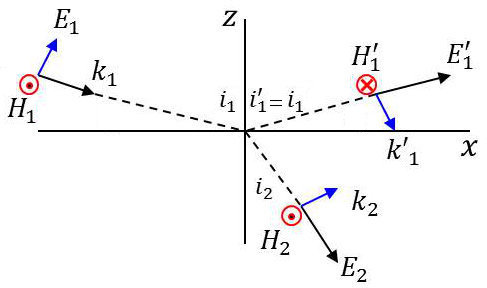Le trièdre \([\overrightarrow{E},~\overrightarrow{H},~\overrightarrow{k}]\) est direct et après réflexion les vecteurs \(\overrightarrow{E}\) et \(\overrightarrow{H}\) changent de sens.

Nous prenons le plan \(xOy\) comme plan d’incidence.

Le champ électrique peut s’écrire sous la forme : \[\overrightarrow{E}=E_0~\exp(j~\omega~t)~\exp(-j~\overrightarrow{k}\cdot\overrightarrow{r})\]

L’expression analytique des amplitudes des champs incident, direct et transmis s’écrivent :

\[\begin{aligned} E_1&=E_{0_1}~\exp\big\{-j~\frac{2~\pi}{\lambda_1}~(\alpha_1~x+\gamma_1~z)\big\}\\ E'_1&=E'_{0_1}~\exp\big\{-j~\frac{2~\pi}{\lambda_1}~(\alpha'_1~x+\beta'_1+\gamma'_1~z)\big\} \\ E_2&=E_{0_2}~\exp\big\{-j~\frac{2~\pi}{\lambda_2}~(\alpha'_2~x+\beta_2+\gamma_2z)\big\}\end{aligned}\]

À l’interface (\(z=0\)), les conditions de continuité permettent d’écrire : \[\beta_2=\beta'_1=0\qquad\text{et}\qquad \frac{\alpha_2}{\lambda_2}=\frac{\alpha'_1}{\lambda_1}=\frac{\alpha_1}{\lambda_2}\]

La première relation montre que les trois plans d’incidence, de réflexion et de réfraction sont confondus.

La relation  \(\alpha'_1=\alpha_1~\Rightarrow~\sin(i'_1)=\sin(i_1)\)  montre que  \(i'_1=i_1\).

On sait par ailleurs que \(\lambda\) est inversement proportionnelle à \(n\). On a donc : \[\frac{\alpha_2}{\lambda_2}=\frac{\alpha_1}{\lambda_1}\qquad\Rightarrow\qquad n_1~\sin(i_1)=n_2~\sin(i_2)\]

On retrouve en définitive les lois de Descartes : \[\left\{ \begin{aligned} i'_1&=i_1\\ n_1~\sin i_1&=n_2~\sin i_2 \end{aligned} \right.\]

2.1. Coefficients d’amplitude

Nous exprimons la continuité des composantes tangentielles de \(\overrightarrow{E}\) et de \(\overrightarrow{H}\) à la surface de séparation des milieux [1]et [2] :

\[\begin{aligned} H_1-H'_1&=H_2 &&(1)\\ E_1~\cos i_1+E'_1~\cos i_1&=E_2~\cos i_2 &&(2)\end{aligned}\]

Nous savons par ailleurs que : \[H=\sqrt{\frac{\varepsilon}{\mu}}~E\qquad\text{et}\qquad n_1=\sqrt{\frac{\varepsilon_1}{\varepsilon_0}}\quad;\quad n_2=\sqrt{\frac{\varepsilon_2}{\varepsilon_0}}\]

D’autre part, les milieux ne sont pas magnétiques, c’est-à-dire que : \[\mu_1=\mu_2=\mu_0\]

La relation (1) devient : \[\sqrt{\varepsilon_1}~(E_1-E'_1)=\sqrt{\varepsilon_2}~E_2 \qquad\qquad\qquad(1')\]

2.1.1. Coefficient de réflexion

Éliminons \(E_2\) entre les relations (1) et (1’) : \[n_1~(E_1-E'_1)=n_2~\frac{\cos i_1}{\cos i_2}~(E_1+E'_1)\]

Or, d’après la loi de Descartes : \[\frac{n_1}{n_2}=\frac{\sin i_2}{\sin i_1}\]

On a donc :

\[\begin{aligned} \sin i_2~\cos i_2~(E_1-E'_1)&=\sin i_1~\cos i_1~(E_1+E'_1)\\ E'_1~(\sin 2~i_1+\sin 2~i_2)&=E_1~(\sin 2i_2-\sin 2~i_1)\end{aligned}\]

Soit : \[E'_1~\{\sin(i_1+i_2)~\cos(i_1-i_2)\}=E_1~\{\sin(i_1-i_2)~\cos(i_1+i_2)\}\]

D’où l’expression du coefficient de réflexion : \[r_{\parallel}=\frac{E'_1}{E_1}=\frac{\tan(i_2-i_1)}{\tan(i_1+i_2)}\]

2.1.2. Coefficient de transmission

Éliminons \(E'_1\) entre les équations (1’) et (2) :

\[\begin{aligned} n_1~E_1-n_2~E_2&=n_1E'_1\\ E_1~\cos i_1-E_2~\cos i_2&=-E'_1~\cos i_1\end{aligned}\]

Tous calculs faits, on obtient : \[4~E_1=E_2~\frac{\sin 2~i_2+\sin 2~i_1}{\sin i_2~\cos i_1}= 2~E_2~\frac{\sin(i_1+i_2)~\cos(i_1+i_2)}{\sin i_2~\cos i_1}\]

D’où l’expression du coefficient de transmission : \[t_{\parallel}=\frac{E_2}{E_1}=\frac{2~\sin i_2~\cos i_1}{\sin(i_1+i_2)~\cos(i_2-i_1)}\]

2.2. Coefficients d’énergie

2.2.1. Coefficient de réflexion

Le coefficient de réflexion en énergie \(R\) est égal au rapport entre la densité d’énergie contenue dans l’onde incidente à celle contenue dans l’onde réfléchie : \[R=\frac{\varepsilon_1~E_1'~E_1'^{*}}{\varepsilon_1~E_1~E_1^{*}} = \Big(\frac{E_1'}{E_1}\Big)~\Big(\frac{E_1'}{E_1}\Big)^{*} = r~r^{*}\]

On a donc : \[R=r~r^{*}\quad (r\in\mathbb{C}) \qquad\text{et}\qquad R=r^2\quad (r\in\mathbb{R})\]

2.2.2. Coefficient de transmission

Le coefficient de transmission en énergie est désigné par \(T\). On sait que la vitesse de propagation est \(v=1/\sqrt{\varepsilon~\mu}\).

Les densités d’énergie dans les milieux [1] et [2] sont respectivement : \[\varepsilon_1~E_1~E_2^{*}\qquad;\qquad \varepsilon_2~E_2~E_2^{*}\]

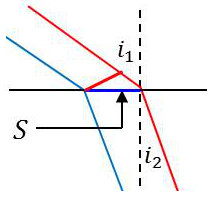
Les flux d’énergie incident et transmis sont respectivement :

\[\begin{aligned} &(\varepsilon_1~E_1~E_1^{*})~\frac{1}{\sqrt{\varepsilon_1~\mu_1}}~(S~\cos i_1)\\ &(\varepsilon_2~E_2~E_2^{*})~\frac{1}{\sqrt{\varepsilon_2~\mu_2}}~(S~\cos i_2)\end{aligned}\]

Faisant le rapport des deux flux : \[T=\Big(\frac{E_2}{E_1}\Big)^{*}~\Big(\frac{E_2}{E_1}\Big)~\frac{\cos i_2}{\cos i_1}~\sqrt{\frac{\varepsilon_2}{\varepsilon_1}}\]

Or on sait que : \[\sqrt{\frac{\varepsilon_2}{\varepsilon_1}}=\frac{n_2}{n_1}=\frac{\sin i_1}{\sin i_2}\]

On a donc : \[T=t~t^*~\frac{\tan i_1}{\tan i_2}\quad(t\in\mathbb{C})\qquad\text{et}\qquad T=t^2\quad(t\in\mathbb{R})\]

Par ailleurs, compte tenu de la relation liant \(E\) et \(H\) : \[T=\frac{E_2~H_2^*~\cos i_2}{E_1~H_1^*~\cos i_1}\]

2.3. Conservation de l’énergie

Nous avions écrit que :

\[\begin{aligned} H_1-H'_1&=H_2 &&(1)\\ E_1~\cos i_1+E'_1~\cos i_1&=E_2~\cos i_2 &&(2)\end{aligned}\]

En passant aux parties conjuguées : \[H_1^*-{H'_1}^*=H_2^* \qquad\qquad\qquad(1^*)\]

En effectuant la multiplication membre à membre \((1^*)\) par \((2)\) : \[E_1~H_1^*~\cos i_1-E'_1~{H'_1}^*~\cos i_1+(E'_1~H_1^*-E_1~{H'_1}^*)~\cos i_1=E_2~H_2^*~\cos i_2\]

Au facteur près \(S/\sqrt{\mu}\) que l’on peut introduire dans les deux membres de cette relation, le premier terme représente le flux incident, le deuxième le flux réfléchi et le quatrième le flux transmis.

D’après le principe de conservation de l’énergie, on doit avoir : \[E'_1~H_1^*-E_1~{H'_1}^*\]

3. Vecteur E perpendiculaire au plan d’incidence

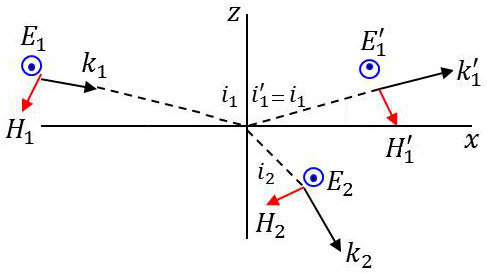Les continuités des composantes tangentielles des champs se traduisent par les relations :

\[\begin{aligned} E_1+E_1'&=E_2\\ H_1~\cos i_1-H'_1~\cos i_1&=H_2~\cos i_2\end{aligned}\]

Tenant compte des relations :

\[\begin{aligned} &\mu_1=\mu_2=\mu_0\\ &\frac{n_1}{n_2}=\sqrt{\frac{\varepsilon_1}{\varepsilon_2}}\quad;\quad H=\sqrt{\frac{\varepsilon}{\mu}}\end{aligned}\]

On est amené à écrire, comme précédemment :

\[\begin{aligned} E_1+E'_1&=E_2\\ n_1~(E_1-E'_1)\cos i_1&=n_2~E_2~\cos i_2=n_2~(E_1+E'_1)~\cos i_2\end{aligned}\]

On en tire : \[\frac{E'_1}{E_1}=\frac{n_1~\cos i_1-n_2~\cos i_2}{n_1~\cos i_1+n_2~\cos i_2}\]

Or : \[\frac{n_1}{n_2}=\frac{\sin i_2}{\sin i_1}\]

Donc : \[\frac{E'_1}{E_1}=\frac{\sin i_2~\cos i_1-\sin i_1~\cos i_2}{\sin i_2~\cos i_1+\sin i_1~\cos i_2}\]

Le coefficient de réflexion en amplitude est donc : \[r_{\bot}=\frac{\sin(i_2-i_1)}{\sin(i_2+i_1)}\]

Reprenons le système :

\[\begin{aligned} E_1+E'_1&=E_2\\ n_1~(E_1-E'_1)~\cos i_1&=n_2~E_2~\cos i_2=n_2~(E_1+E'_1)~\cos i_2\end{aligned}\]

Puis, tous calculs faits, comme précédemment : \[t_{\bot}=\frac{2~\sin i_2~\cos i_1}{sin(i_1+i_2)}\]

Remarque

Tout ce qui a été dit dans le paragraphe précédent en ce qui concerne l’énergie se retrouve ici intégralement. En particulier pour les coefficients : \[R=r~r^*\qquad;\qquad T=t~t^*~\frac{\tan i_1}{\tan i_2}\]

Le principe de conservation de l’énergie conduit aussi à : \[E'_1~H_1^*-E_1~{H'_1}^*=0\]

Ce principe permet d’écrire dans tous les cas : \[R+T=1\]

4. Cas particulier : incidence normale

En incidence normale, il n’y a plus lieu de faire la distinction entre \(E_{\bot}\) et \(E_{\parallel}\). Rien ne permet de distinguer les deux cas.

On pose \(i_1=i_2=0\) avant d’appliquer les formules de Descartes de façon à lever l’indétermination. On obtient alors (formules de Fresnel) : \[r=\frac{n_i-n_2}{n_1+n_2}\qquad;\qquad t=\frac{2~n_1}{n_1+n_2}\]

5. Variation du pouvoir réflecteur avec l’incidence

5.1. Incidence brewstérienne

Reprenons l’expression : \[r_{\parallel}=\frac{E'_1}{E_1}=\frac{\tan(i_2-i_1)}{\tan(i_2+i_1)}\]

On voit que : \[r_{\parallel}=0\quad\Rightarrow\quad i_1+i_2=\frac{\pi}{2}\]

Le rayon réfléchi et le rayon réfracté sont alors perpendiculaires. L’angle \(i_1=i_B\) pour lequel cela se produit est dit incidence brewstérienne : \[n_1~\sin i_1=n_2~\sin i_2=n_2~\sin\Big(\frac{\pi}{2}-i_1\Big)=n_2~\cos i_1\]

L’incidence brewstérienne est alors définie par : \[\tan i_B=\frac{n_2}{n_1}\]

5.2. Réflexion vers un milieu plus réfringent

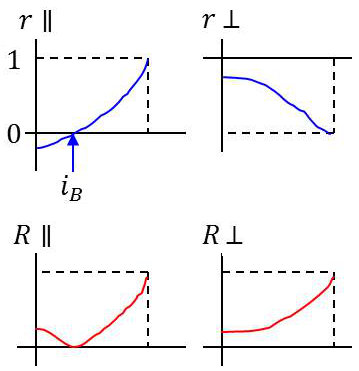Dans le cas de réflexion vers un milieu moins réfringent, comme le dioptre air – verre :

\[\begin{aligned} &r_{\parallel}=\frac{\tan(i_2-i_1)}{\tan(i_2+i_1)}\quad;\quad R_{\parallel}=r_{\parallel}^2\\ &r_{\bot}=\frac{\sin(i_2-i_1)}{\sin(i_2+i_1)}\quad;\quad R_{\bot}=r_{\bot}^2\end{aligned}\]

D’où les courbes ci-contre dans lesquelles l’ordonnée non mentionnée pour \(r_{\parallel}\) et \(r_{\bot}\) a pour valeur : \[\frac{n_1-n_2}{n_1+n_2}\]

On a toujours \(i_1>i_2\).

À l’incidence brewstérienne : \[i_1+i_2=\frac{\pi}{2}\]

On a :

\[\begin{aligned} &i_1<i_B\quad;\quad i_1+i_2<\frac{\pi}{2}\quad;\quad \tan(i_1+i_2)>0\quad;\quad \tan(i_2-i_1)<0\\ &i_1>i_B\quad;\quad i_1+i_2>\frac{\pi}{2}\quad;\quad \tan(i_1+i_2)>0\quad;\quad \tan(i_2-i_1)<0\end{aligned}\]

Remarquer que : \[i_1=\frac{\pi}{2}\quad\rightarrow\quad \tan(i_2\pm\frac{\pi}{2})=\cot i_2\]

Par suite : \(r_{\parallel}=1\).

On peut facilement tracer la courbe \(r_{\parallel}\) et en déduire \(R=r^2\). On effectue le même raisonnement pour \(r_{\bot}\) et en déduire \(R_{\bot}\).

5.3. Déphasage à la réflexion

On peut écrire : \[r_{\parallel}=\frac{\tan(i_2-i_1)}{\tan(i_2+i_1)}=\rho.e^{j\varphi}\]

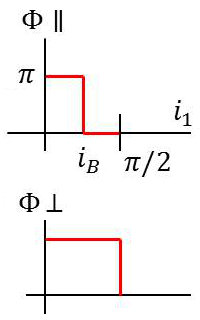L’examen de la courbe montre que :

\[\begin{aligned} &0<i_1<i_B\quad r_{\parallel}<0\quad r_{\parallel}=\rho.e^{j\pi}\\ &i_B<i_1<\frac{\pi}{2}\quad r_{\parallel}>0\quad r_{\parallel}=rho\end{aligned}\]

D’où la courbe du déphasage \(\varphi(i_1)\).

On peut également écrire : \[r_{\bot}=\frac{\sin(i_2-i_1)}{\sin(i_2+i_1)}=\rho.e^{j\varphi}\]

On voit que (courbe) : \[0<i_1<\frac{\pi}{2}\quad r_{\bot}<0\quad r_{\bot}=\rho.e^{j\pi}\]

5.4. Réflexion vers un milieu moins réfringent

Dans le cas de réflexion vers un milieu moins réfringent, comme le dioptre verre - air, le problème est le complémentaire du précédent, mais cependant bien plus complexe en raison du phénomène de réflexion totale.

5.4.1. Réflexion totale. Ondes évanescentes

On sait que l’angle limite \(l\) est obtenu par la relation  \( \sin l=\cfrac{n_2}{n_1} \) et qu’il y a réflexion totale lorsque  \(i_1>l\).

Par ailleurs : \[\sin i_2=\frac{n_1}{n_2}~\sin i_1=\frac{1}{n}~\sin i_1\qquad(n<1)\]

On voit alors que : \[\frac{\sin i_1}{n}>l\quad\text{si:}~~i_1>l\quad\Rightarrow\quad i_2\in\mathcal{J}\]

On aura alors : \[\cos i_2=\sqrt{1-\frac{\sin^2i_1}{n^2}}=\pm j~\sqrt{\frac{\sin^2i_1}{n^2}-1} \qquad(\text{on posera : }\cos i_2=\pm j~m)\]

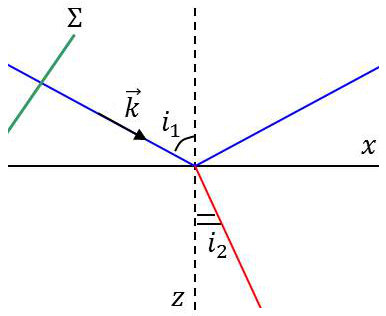On considère l’onde passant dans le milieu [2] : \[E_2=E_{02}~\exp(-j~\overrightarrow{k}\cdot\overrightarrow{r})\]

Avec les notations suivantes :

\[\begin{aligned} \overrightarrow{r}&=\{x,~y,~z\}\\ \overrightarrow{k}&=\Big\{\frac{2~\pi}{\lambda}~\sin i_2,~0,~\frac{2~\pi}{\lambda}~\cos i_2\Big\} \\ \overrightarrow{k}\cdot\overrightarrow{r}&=x~\frac{2~\pi}{\lambda}~\sin i_2\pm z~\frac{2~\pi}{\lambda}~j~m\end{aligned}\]

On a donc : \[E_2=E_{02}~\exp\big(\pm\frac{2~\pi}{\lambda}~m~z\big)~\exp\big(-j~\frac{2~\pi}{\lambda}~x~\sin i_2\big)\]

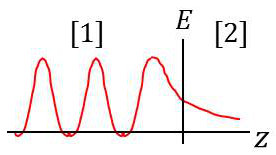Pour l’amplitude qui contient le terme de phase \(\cfrac{2~\pi}{\lambda}~m~z\), il doit y avoir logiquement décroissance exponentielle quand on s’éloigne de la surface de séparation.

Il faut prendre le signe [–], c’est-à-dire que : \[\cos i_2=-j~m\]

C’est ce que l’on appelle une onde évanescente. Cette onde transmise a un sens et il est nécessaire de la considérer pour assurer la continuité de \(\overrightarrow{E}\) et \(\overrightarrow{H}\).

On ne peut pas concevoir que le champ électrique devienne brutalement nul après avoir atteint la surface de séparation. Pour \(z\) assez grand, il y a réellement réflexion totale, l’onde tendant à disparaître, sinon il y a réflexion totale frustrée.

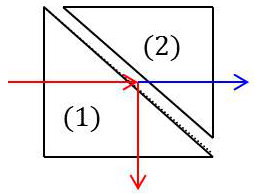Cette onde peut être mise en évidence par l’expérience suivante. On rapproche l’un de l’autre deux prismes à réflexion totale de façon à donner à la lame d’air qui les sépare une épaisseur de l’ordre de \(\lambda\).

Au contact du prisme (1), l’onde évanescente provenant du prisme (1) a une amplitude non négligeable.

5.4.2. Étude des coefficients de réflexion

On sait que :

\[\begin{aligned} &r_{\parallel}=\frac{\tan(i_2-i_1)}{\tan(i_2+i_1)}\quad;\quad R_{\parallel}=r_{\parallel}^2\\ &r_{\bot}=\frac{\sin(i_2-i_1)}{\sin(i_2+i_1)}\quad;\quad R_{\bot}=r_{\bot}^2\end{aligned}\]

Dans le cas présent : \[i_2>i_1\qquad i_2-i_1>0\]

Nous avons donc les cas suivants : \[\left\{ \begin{aligned} &0<i_1<i_B\quad;\quad i_1+i_2<\frac{\pi}{2}\quad;\quad\tan(i_1+i_2)>0\\ &r_{\parallel}>0\quad;\quad r_{\parallel}=\rho \end{aligned} \right.\] \[\left\{ \begin{aligned} &i_B<i_1<l \quad;\quad i_1+i_2>\frac{\pi}{2} \quad;\quad \tan(i_1+i_2)<0\\ &r_{\parallel}<0\quad;\quad r_{\parallel}=\rho~e^{j~\pi} \end{aligned} \right.\]

Or, on a : \[i_2>i_1 \quad;\quad i_1+i_2<\pi \quad;\quad r_{\bot}>0\]

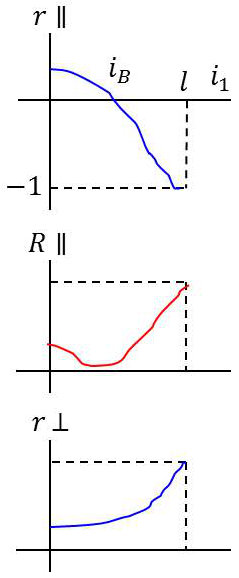Étudions à présent ces deux coefficients à la réflexion totale : \[r_{\bot}=\frac{\sin i_2~\cos i_1-\sin i_1~\cos i_2}{\sin i_2~\cos i_1+\sin i_1~\cos i_2}= \frac{\sin i_2~\cos i_1+j~m~\sin i_1}{\sin i_2~\cos i_1-j~m~\sin i_1}\]

Numérateur et dénominateur étant imaginaires conjugués \(r_{\bot}=1\), d’où la valeur \(r_{\bot}=1\) pour \(i_1=l\) sur la courbe : \[r_{\parallel}=\frac{\sin i_2~\cos i_2-\sin i_1~\cos i_1}{\sin i_2~\cos i_2+\sin i_1~\cos i_1}= -\frac{j~m~\sin i_2+\sin i_1~\cos i_1}{-j~m~\sin i_2+\sin i_1~\cos i_1}\]

En faisant la même remarque que précédemment, on a : \[|r_{\parallel}|=1\]

mais sur la courbe, on aura : \[r_1=1\quad\text{pour}~~i_1=l\]

Les courbes \(R\) se déduisent facilement des courbes \(r_{\bot}\) et \(r_{\parallel}\).

5.4.3. Étude des déphasages

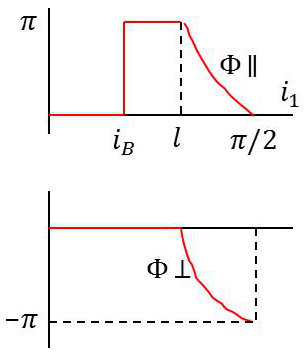Pour savoir ce qui se passe au-delà de \(l\), on reprend l’expression : \[r_{\parallel}=-\frac{j~m~\sin i_2+\sin i_1~\cos i_1}{-j~m~\sin i_2+\sin i_1~\cos i_1}=e^{j~\pi}~e^{j~\varphi}\]

Ou encore : \[\tan\Big(\frac{\varphi}{2}+\frac{\pi}{2}\Big)=\frac{m~\sin i_2}{\sin i_1~\cos i_1}\]

On voit que : \[i_1=\frac{\pi}{2}\quad\Rightarrow\quad\tan\Big(\frac{\varphi}{2}+\frac{\pi}{2}\Big)=\infty \quad\Rightarrow\quad\varphi=0\]

Pour savoir ce qui se passe au-delà de \(l\), on reprend l’expression : \[r_{\bot}=\frac{\sin i_2~\cos i_1+j~m~\sin i_1}{\sin i_2~\cos i_1-j~m~\sin i_1}=e^{j~\varphi} \quad;\quad \tan\frac{\varphi}{2}=\frac{m~\sin i_1}{\sin i_2~\cos i_1}\]

Ainsi : \[i_1=\frac{\pi}{2}~~;~~\tan\frac{\varphi}{2}=\infty\quad\Rightarrow\quad \frac{\varphi}{2}=\pm\frac{\pi}{2}~~;~~\varphi=\pm\pi\]