1. Caractéristiques du cristal uniaxe
Nous avons dit qu’un cristal était uniaxe si deux constantes diélectriques étaient égales, par exemple : \[\varepsilon_x=\varepsilon_y\neq\varepsilon_z\quad\Rightarrow\quad n_x=n_y\neq n_z\]
L’ellipsoïde des indices est alors de révolution autour de \(Oz\) puisque son équation devient : \[\frac{x^2+y^2}{n_x^2}+\frac{z^2}{n_z^2}=1\]
L’axe de symétrie \(Oz\) se confond avec l’axe optique.
Quel que soit son état de polarisation, une onde dont le plan est perpendiculaire à l’axe optique d’un milieu uniaxe s’y propage exactement de la même façon que dans un milieu isotrope.
L’indice correspondant à une vibration perpendiculaire à l’axe optique est dit ordinaire : \[n_o=n_x=n_y\]
L’indice correspondant à une vibration parallèle à l’axe optique est dit extraordinaire : \[n_e=n_z\]
L’équation de l’ellipsoïde devient : \[\frac{x^2+y^2}{n_o^2}+\frac{z^2}{n_e^2}=1\]
Si \(n_e-n_o>0\), le cristal est dit positif. Il est dit négatif dans le cas contraire.
2. Propagation d’une onde plane
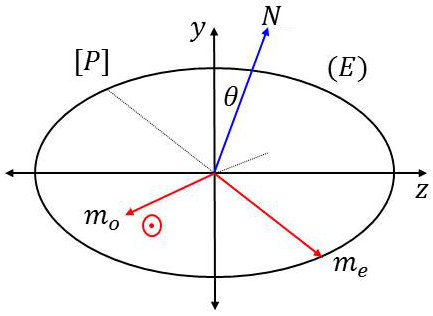Soit \([P]\) le plan d’onde dont la normale \(N\) fait un angle \(\theta\) quelconque avec l’axe \(Oy\). Il découpe l’ellipsoïde suivant une ellipse [\(\gamma\)] vue en coupe suivant le vecteur \(m_e\).
Pour la vibration \(\overrightarrow{Om_0}\) perpendiculaire à l’axe optique, tout se passe comme si elle rencontrait un milieu isotrope d’indice ordinaire \(n_o\).
Sa vitesse de propagation est la vitesse ordinaire \(v_o=\cfrac{c}{n_0}\).
La deuxième vibration \(\overrightarrow{Om_e}\) est appelée vibration extraordinaire. L’indice \(n\) qui lui correspond est l’indice extraordinaire.
Il est égal au rayon \(Om_e\), mais on a \(n_0<n<n_e\), ce dernier \(n_e\) étant l’indice extraordinaire principal. Cette valeur ne dépend que de la direction de \([P]\).
Plaçons-nous dans le plan méridien \(yOz\). L’équation de la méridienne est : \[\frac{y^2}{n_o^2}+\frac{z^2}{n_e^2}=1\]
En remarquant que : \[|y|=n~\sin\theta\quad;\quad|z|=n~\cos\theta\]
l’équation devient : \[n^2~\Big(\frac{\sin^2\theta}{n_o^2}+\frac{\cos^2\theta}{n_e^2}\Big)=1\]
Par ailleurs :
\[\begin{aligned} v&=\frac{c}{n}\quad;\quad v-e=\frac{c}{n_e}\quad;\quad v_o=\frac{c}{n_o}\\ v^2&=v_0^2~\sin^2\theta+v_e^2~\cos^2\theta\quad\Rightarrow\quad v^2-v_0^2=(v_e^2-v_0^2)~\cos^2\theta\end{aligned}\]
Deux cas peuvent se présenter :
\[\begin{aligned} [P]~\bot~Oz~~&:\quad\theta=\frac{\pi}{2}\quad\Rightarrow\quad v=v_o\quad;\quad n=n_o\\ [P]~\parallel~Oz~~&:\quad\theta=\pi~\quad\Rightarrow\quad v=v_e\quad;\quad n=n_e\end{aligned}\]
3. Surface des indices
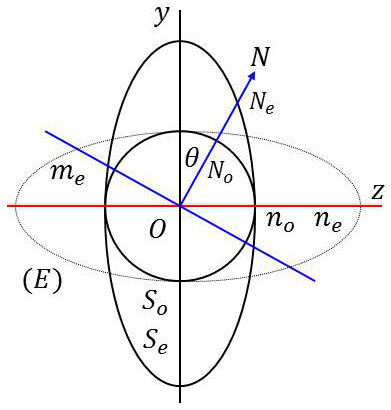La surface des indices est obtenue point par point en portant sur la normale au plan \([P]\) les deux longueurs : \[ON_o=n_o\quad;\quad ON_e=n\]
La première est indépendante de l’orientation de \([P\)] : c’est la sphère \([S_o]\). La deuxième nappe est du quatrième degré, mais elle n’a pas de point à l’infini : c’est un ellipsoïde de révolution autour de l’axe optique, car le système possède une symétrie de révolution du point de vue optique.
Les points communs aux deux nappes se réduisent aux points situés sur l’axe optique et elles sont tangentes. Les ellipses \([E]\) et \([S_e]\) sont égales, mais orientées à \(\pi/2\) l’une par rapport à l’autre.
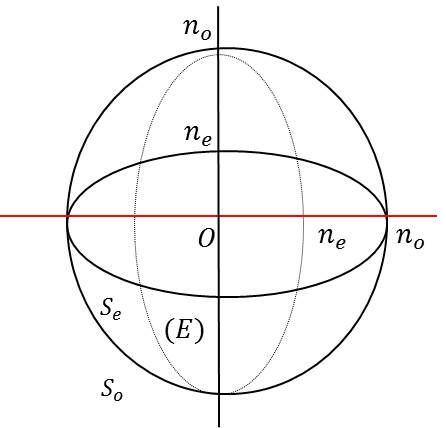La figure du haut correspond au cas d’un cristal positif (\(n_e>n_o\)) alors que celle du bas correspond au cas d’un cristal négatif.
Note : Nous avons vu que l’indice était donné par la relation : \[n^2~\Big(\frac{\sin^2\theta}{n_o^2}+\frac{\cos^2\theta}{n_e^2}\Big)=1\]
Coordonnées de \(N_e\) : \( z=n~\cos\theta\quad;\quad y=n~\sin\theta \)
Équation de \(S_e\) : \(\qquad\cfrac{z^2}{n_2}+\cfrac{y^2}{n_2}=1 \)
4. Réfraction dans les cristaux
La réfraction dans les cristaux est plus complexe que dans les milieux isotropes. On a vu qu’il y avait deux nappes pour les surfaces d’onde, donc un rayon passant d’un milieu isotrope dans un milieu anisotrope va subir le phénomène de double réfraction : il y aura un rayon ordinaire et un rayon extraordinaire.
4.1. Construction de Descartes
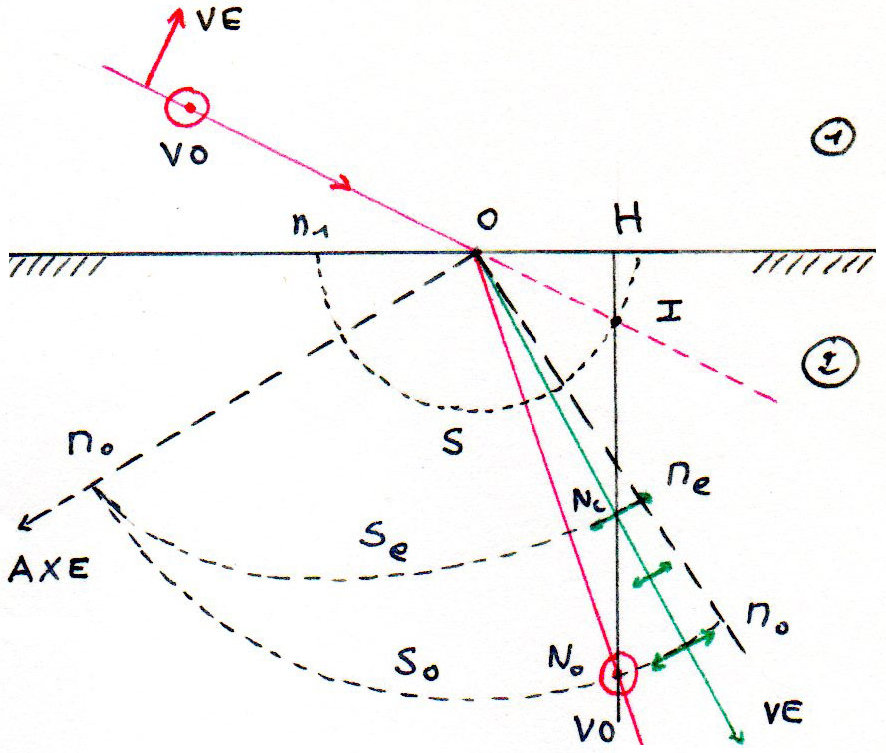Le milieu (1) est supposé isotrope ; on se donne l’axe optique du milieu (2) supposé négatif (\(n_e<n_o\)).
Relativement au milieu (1), la surface des indices est \(S\), sphère de centre \(O\) et de rayon \(n_1\) .
Relativement au milieu (2), les surfaces des indices sont \(S_o\), sphère de centre \(O\) et rayon \(n_o\) et \(S_e\), ellipse de demi-axes \(n_o\) et \(n_e\), le premier étant porté par l’axe optique.
Le prolongement du rayon incident coupe \(S\) en \(I\). En ce point, on élève la perpendiculaire \(IH\) à la surface de séparation : elle coupe \(S_o\) en \(N_o\) et \(S_e\) en \(N_e\). On joint \(On_o\) et \(On_e\) qui sont les deux rayons réfractés.
Note : Si l’axe optique était perpendiculaire au plan d’incidence, toutes les surfaces des indices seraient des sphères. On remarque par ailleurs que la vibration ordinaire est toujours perpendiculaire à l’axe.
4.2. Construction de Huyghens
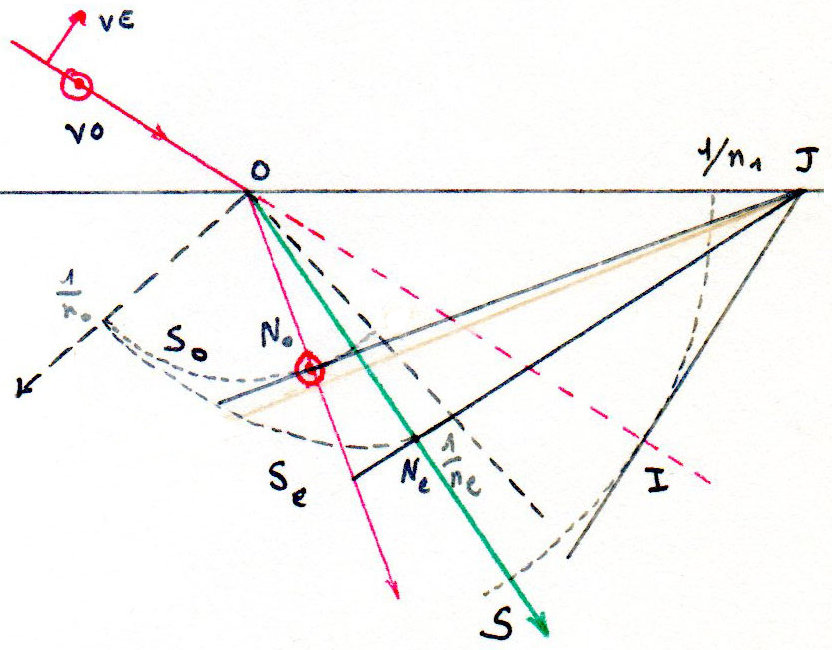On trace les surfaces des indices comme précédemment, à cette différence près que le petit axe de l’ellipse est porté par l’axe optique car on effectue le changement : \[n_1~\rightarrow~\frac{1}{n_1}\quad;\quad n_o~\rightarrow~\frac{1}{n_o}\quad;\quad n_e~\rightarrow~\frac{1}{n_e}\]
Le prolongement du rayon incident coupe \(S\) en \(I\). La tangente en \(I\) à \(S\) coupe la surface de réparation en \(J\).
De \(J\), on mène les tangentes \(J_{no}\) et \(J_{ne}\) aux surfaces \(S_o\) et \(S_e\), d’où les rayons réfractés.
Note : Si l’axe optique était perpendiculaire au plan d’incidence, toutes les surfaces seraient des sphères.
