1. Lumière naturelle et lumière polarisée
Dans l’étude des milieux isotropes, nous avions vu que les vecteurs \(\overrightarrow{E}\) (ou \(\overrightarrow{H}\)) étaient animés d’un mouvement rectiligne sinusoïdal : la vibration était polarisée et rectiligne, le plan de vibration étant le plan \((\overrightarrow{E},\overrightarrow{v})\).
Or, toute source lumineuse est formée d’un grand nombre d’atomes émettant des vibrations dont les phases et les directions sont distribuées aléatoirement. La lumière naturelle est donc la superposition d’un grand nombre de vibrations rectilignes dont les phases et les directions sont réparties aléatoirement. Elle n’est caractérisée par aucun plan de vibration privilégié comme le sont les vibrations rectilignes.
Un polariseur est un dispositif capable de transformer la lumière naturelle en lumière polarisée : en fait, il ne s’agit pas d’une transformation, mais d’une sélection. Le polariseur est caractérisé par une direction privilégiée, celle des vibrations qu’il transmet, et il arrête les vibrations perpendiculaires.
Un analyseur est un dispositif capable de déterminer si une lumière est polarisée ou non et de déterminer la direction de vibration. Un analyseur est donc tout simplement un polariseur que l’on fait traverser par la lumière à analyser. Si l’on peut produire une extinction, c’est que la lumière est polarisée totalement et rectiligne et l’azimut du polariseur qui produit l’extinction permet de connaître la direction de vibration.
2. Quelques types de polariseurs
2.1. Polarisation par réflexion vitreuse
Attaquée sous l’incidence brewstérienne, une simple lame de verre constitue un polariseur élémentaire : \[\tan i=\frac{n_2}{n_1}=n\]
On sait que la composante perpendiculaire au plan d’incidence est seule réfléchie et que rayon réfléchi et rayon réfracté sont perpendiculaires. Environ 15 % de la vibration incidente convenable sont réfléchis.
2.2. Polariseur à double réfraction
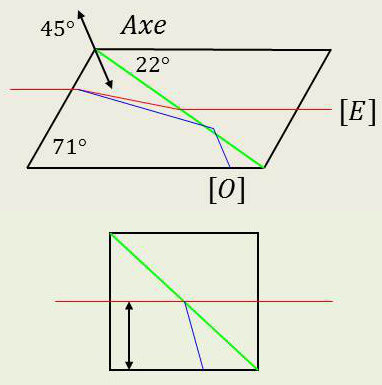Le prisme de Nicols est un polariseur à double réfraction. Il est constitué par un cristal de spath de longueur convenable et scié suivant une section diagonale. Les deux moitiés sont ensuite recollées avec une couche de baume de Canada.
On choisit la valeur angulaire de 22 ° de sorte que \(V_e\) subisse une réflexion totale et soit ensuite redressée dans la deuxième partie du prisme pour être, à la sortie du prisme, parallèle au rayon incident.
Il n’y a cette fois aucune perte d’énergie sur le rayon extraordinaire.
Citons également le prisme de Glazebrook, réplique du prisme de Nicols. Cette fois, le champ est normal, c’est-à-dire que le rayon moyen est normal à la face d’entrée.
2.3. Dispositifs biréfringents
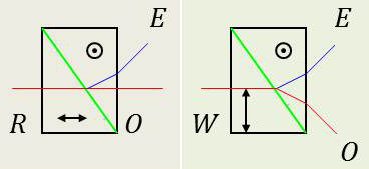On a quelque fois besoin de biréfringents transmettant les faisceaux \(O\) et \(E\) avec une séparation angulaire.
Tels sont les prismes de Rochon et de Wollaston réalisés en quartz.
2.4. Polariseurs à dichroïsme. Polaroïdes
Certaines substances sont absorbantes et ont la propriété de ne pas absorber de manière égale les \(V_o\) et les \(V_e\) : on dit qu’elles sont dichroïques. Cette propriété est connue depuis très longtemps pour la tourmaline.
On fait encore mieux avec les cristaux d’hérapathite ou iodosulfate de quinine. Ces cristaux microscopiques sont noyés en grande quantité dans une feuille de plastique transparent et orientés par un procédé convenable, de sorte que leurs axes soient parallèles. On obtient des feuilles polarisantes aussi grandes que l’on veut : ce sont les polaroïdes.
3. Biréfringences provoquées
Un matériau primitivement isotrope peut devenir anisotrope sous l’action de causes extérieures. Le milieu devient uniaxe et cet axe optique est parallèle à la direction de la cause extérieure. La biréfrigence croît avec cette cause.
3.1. Biréfringence d’origine mécanique
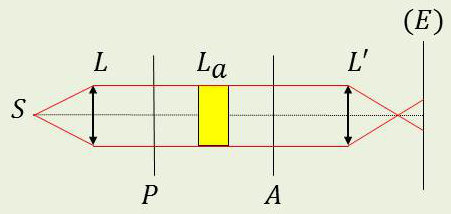Une lame de verre (isotrope, car c’est un solide amorphe) est placée entre deux polariseurs croisés.
Le plan d’observation (écran \(E\)) est conjugué de la lame \(L_a\) par rapport à la lentille \(L'\).
Si on comprime \(L_a\), la lumière réapparaît en \(E\), aux points conjugués de ceux de \(L_a\), où la biréfrigence se manifeste.
Si la compression est bien uniforme, la lumière réapparaît uniformément. Toutefois, elle ne réapparaît que si la direction de l’effort est parallèle ou perpendiculaire à l’azimut du polariseur.
Ceci prouve que l’une des lignes neutres de la lame est parallèle à la direction de l’effort. \(P\) désignant la pression, les mesures montrent que : \[n_e-n_0=k~P\]
3.2. Biréfringence d’origine électrique
La biréfringence d’origine électrique constitue l’effet Kerr découvert en 1876. Beaucoup de liquides soumis à un champ électrique \(\overrightarrow{E}\) deviennent uniaxes, la direction de l’axe optique étant celle du champ \(\overrightarrow{E}\).
L’expérience montre que : \[n_o-n_e=B~\lambda~E^2\]
\(B\) : constante de Kerr (positive ou négative).
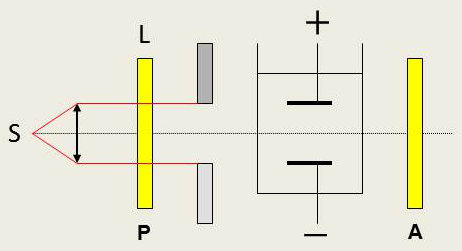Un obturateur de Kerr s’obtient par exemple en appliquant des impulsions de tension à une cellule de Kerr remplie de nitrobenzène (B élevée) et placée entre deux Nicols croisés et placés à 45 ° par rapport à \(\overrightarrow{E}\).
Une série d’impulsions électriques rectangulaires découpe la lumière comme le ferait une roue tournant à grande vitesse et peut être utilisée pour une mesure précise de la vitesse de la lumière suivant une méthode analogue à celle de Fizeau.
3.3. Effet Cotton - Mouton
L’effet Cotton - Mouton a été découvert en 1906. C’est la biréfringence d’origine magnétique. Dans le dispositif précédent, on remplace le condensateur par un aimant et on observe perpendiculairement par rapport à \(\overrightarrow{H}\).
L’axe optique est dirigé suivant le vecteur \(\overrightarrow{H}\).
L’expérience montre que : \[n_e-n_o=C~\lambda~H^2\]
