1. Introduction

Un certain nombre de substances, même isotropes, ont sur la lumière polarisée une action toute différente de la biréfringence. Si la lumière polarisée rectiligne traverse une lame à faces parallèles d’une telle substance, elle est encore polarisée rectiligne à la sortie, mais son azimut de polarisation a tourné d’un certain angle \(\alpha\), indépendant de l’orientation de la direction incidente.

On dit que la substance possède un pouvoir rotatoire ou encore une activité optique.

2. Expérience fondamentale

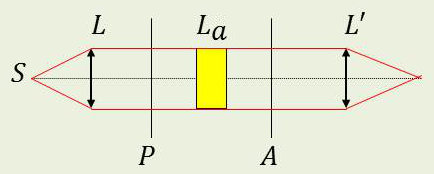La substance à étudier est placée entre polariseur et analyseur croisés. Elle est isotrope et il n’y a pourtant pas extinction.

Si l’on fait tourner la lame autour de l’axe du système, rien ne change. Il ne s’agit donc pas de biréfringence puisqu’aucune direction privilégiée autour de l’axe ne se manifeste dans la lame.

L’extinction est rétablie si on donne à l’analyseur un nouvel azimut : la lame conserve donc la nature rectiligne de la lumière incidente et la fait simplement tourner de \(\alpha\).

L’expérience montre que \(\alpha=\rho~l\), le paramètre \(\rho\) étant une caractéristique de la substance et \(l\) la longueur traversée.

L’observateur regarde la source à travers le système. Si la substance fait tourner le plan de polarisation vers la droite, elle est dite dextrogyre ; dans le cas contraire, elle est dite lévogyre.

Si au lieu de considérer une substance pure, on considère des substances dissoutes, la rotation \(\alpha\) est donnée par la loi de Biot : \[\alpha=\sum_i K_i~l~C_i\]

• \(l\) :   Épaisseur de la solution traversée

• \(C_i\) : Concentration de la solution \(i\)

• \(K_i\) : Constante caractéristique de la substance \(i\)

3. Interprétation de Fresnel

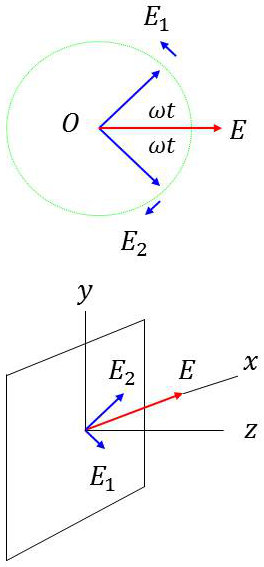Toute vibration rectiligne \(\overrightarrow{E}\) d’amplitude \(a\) peut être considérée comme la somme de deux vibrations circulaires \(\overrightarrow{E_1}\) et \(\overrightarrow{E_2}\) dont l’amplitude est \(a/2\), de même pulsation, mais tournant en sens inverse l’une de l’autre.

La direction de \(\overrightarrow{E}\) est la bissectrice de \((\overrightarrow{E_1},~\overrightarrow{E_2})\).

Considérons une vibration rectiligne \(\overrightarrow{E}\) dirigée suivant \(Ox\) dans le plan \(z=0\). Elle peut être décomposée en deux vibrations circulaires \(\overrightarrow{E_1}\) et \(\overrightarrow{E_2}\) de même amplitude : \[\overrightarrow{E_1}=\overrightarrow{E_0}~\exp(j~\omega~t)\quad;\quad \overrightarrow{E_2}=\overrightarrow{E_0}~\exp(-j~\omega~t)\]

Nous admettons que le milieu a la propriété de transmettre les vibrations circulaires sans altération. Au point de cote \(z\), on aura :

\[\begin{aligned} &\overrightarrow{E'_1}=\overrightarrow{E_0}~\exp\{j~\omega~(t-\frac{z}{v_1})\}\quad;\quad v_1=\frac{c}{n_1}\\ &\overrightarrow{E'_2}=\overrightarrow{E_0}~\exp\{j~\omega~(t-\frac{z}{v_2})\}\quad;\quad v_2=\frac{c}{n_2}\end{aligned}\]

Il apparaît donc un déphasage : \[\varphi=\varphi_1-\varphi_2=\frac{\omega~z}{v_1}-\frac{\omega~z}{v_2}\]

Mais nous savons que : \[\omega=\frac{2\pi}{T}\quad;\quad v=\frac{c}{n}\quad \Rightarrow\quad \frac{\omega}{v}=\frac{2~\pi~n}{c~T}=\frac{2~\pi~n}{\lambda}\]

Le déphasage est donc : \[\varphi=\frac{2~\pi}{\lambda}~(n_1-n_2)~z\]

En supposant \(\varphi>0\), la vibration \(\overrightarrow{E}\) a tourné de \(\alpha=\varphi/2\) dans le même sens que la vibration \(\overrightarrow{E_1}\).

Ainsi le pouvoir rotatoire apparaît comme équivalent à une biréfringence circulaire, \(\overrightarrow{E'}\) tournant dans le sens de la vibration la moins retardée.

Mise en évidence de la biréfringence circulaire

On peut obtenir la biréfringence circulaire de trois manières :

1. Avec un prisme contenant une solution sucrée ;

2. Avec un prisme de quartz au minimum de déviation et taillé de telles sorte que son axe soit parallèle à la base pour ne pas avoir de biréfringence rectiligne (pour un rayon parallèle à l’axe, le quartz se comporte comme un milieu isotrope). On constate qu’il y a deux rayons émergents ;

   On appelle prisme de quartz droit un prisme pour lequel la vibration circulaire gauche correspond au plus grand indice et à la plus grande déviation. Pour un prisme gauche, \(D\) est plus dévié que \(G\).

3. Avec le prisme de Cornu.

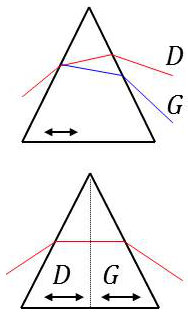La biréfringence circulaire du quartz est assez grande dans les appareils spectraux pour les UV.

On remplace alors le prisme unique par un prisme droit et un prisme gauche.

On rétablit ainsi pour un rayon perpendiculaire au plan de séparation des deux prismes l’égalité des déviations.

4. Polarisation rotatoire magnétique

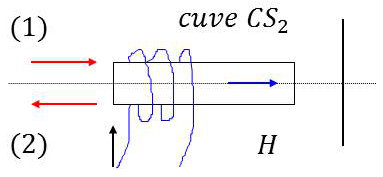La polarisation rotatoire magnétique est ce que l’on appelle encore l’effet Faraday.

Si on soumet certaines substances à une induction magnétique et si on les fait traverser par de la lumière parallèle au champ (c’est ce qui distingue cette expérience de l’effet Cotton - Mouton), on constate qu’elles deviennent actives.

On fait faire un trajet aller - retour à la lumière de sorte que les effets s’ajoutent. L’expérience montre que : \[\alpha=K~l~H\]

\(K\) : constante de Verdenet qui dépend de \(\lambda\)

Le sens de rotation est lié au sens de \(\overrightarrow{H}\) et s’inverse avec lui. Dans le cas le plus fréquent, le sens de rotation est celui de la circulation du courant qui crée le champ \(\overrightarrow{H}\).

Interprétation

L’effet Faraday est lié à la décomposition des raies spectrales (émission ou absorption par le champ magnétique). C’est un effet Zeeman.

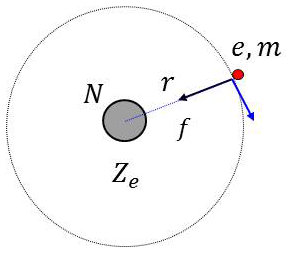
On a déjà écrit, considérant le mouvement de l’électron sur son orbite : \[\frac{1}{4~\pi~\varepsilon_0}~\frac{Ze^2}{r^2}=m~\omega~r\quad\Rightarrow\quad \omega=\frac{1}{4~\pi~\varepsilon_0}~\frac{Z~e^2}{m~r^3}\]

Si l’on fait intervenir une induction \(\overrightarrow{B}\) perpendiculaire au plan de l’orbite, l’électron est soumis à la force de Laplace : \[\overrightarrow{f'}=e~\overrightarrow{v}\wedge\overrightarrow{B}\qquad\text{soit :}\quad f'=e~B~\omega~r\]

On devra écrire : \[m~\omega'~r^2\pm e~B~\omega'~r=m~\omega^2~r\]

Comme \(\omega'\approx\omega\), on posera \(\Delta\omega=\omega'-\omega\).

D’où la nouvelle expression : \[\Delta\omega=\pm\frac{e~B}{2~m}\]

Si l’électron tournait à la vitesse \(\omega\) , on obtiendrait \(\omega+\Delta\omega\quad\) (accélération).

Si l’électron tournait à la vitesse \(-\omega\) , on obtiendrait \(-(\omega-\Delta\omega)=-\omega+\Delta\omega\quad\) (retard).